| Citation: |
Ahlem BenRabah, Omar Abu Arqub. AN EFFECTIVE SUSTAINABLE COLLOCATION METHOD FOR SOLVING REGULAR/SINGULAR SYSTEMS OF CONFORMABLE DIFFERENTIAL EQUATIONS SUBJECT TO INITIAL CONSTRAINT CONDITIONS[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1336-1358. doi: 10.11948/20220138
|
AN EFFECTIVE SUSTAINABLE COLLOCATION METHOD FOR SOLVING REGULAR/SINGULAR SYSTEMS OF CONFORMABLE DIFFERENTIAL EQUATIONS SUBJECT TO INITIAL CONSTRAINT CONDITIONS
-
Abstract
The main objective of the present article is to provide an overview of the B-splines collocation methods (BSCM) to achieve practical analytical-numerical solutions for a family of regular/singular systems of initial constraints condition (ICC). Herein, the fractional derivatives are described by the conformable one, and an abundance of its basic theory is utilized. The useful properties of the cubic B-splines and collocation methods are employed to reduce the computations of both regular/singular systems of fractional order to a combination of linear/nonlinear algebraic equations. Numerical tests are treated quantitatively to demonstrate the technical statements and to exhibit the ability, perfection, and applicability of the suggested procedure for solving such conformable systems models. The outcomes confirm the reliability and efficacy of the technique improved. At the end of the manuscript, some notes were presented with some characteristics of the scheme and some possible future work.
-
-
References
[1] S. Arshed, B-spline solution of fractional integro partial differential equation with a weakly singular kernel, Numerical Methods for Partial Differential Equations, 2017, 33, 1565-1581. doi: 10.1002/num.22153 [2] T. Abdeljawad, On conformable fractional calculus, Journal of Computational and Applied Mathematics, 2015, 279, 57-66. doi: 10.1016/j.cam.2014.10.016 [3] Y. Çenesiz, A. Kurt and E. Nane, Stochastic solutions of conformable fractional Cauchy problems, Statistics & Probability Letters, 2017, 124, 126-131. [4] W. S. Chung, S. Zare and H. Hassanabadi, Investigation of conformable fractional Schrodinger equation in presence of killingbeck and hyperbolic potentials, Communications in Theoretical Physics, 2017, 67, 250-254. doi: 10.1088/0253-6102/67/3/250 [5] C. Chen and Y. Jiang, Simplest equation method for some time-fractional partial differential equations with conformable derivative, Computers & Mathematics with Applications, 2018, 75, 2978-2988. [6] N. Caglar and H. Caglar, B-spline method for solving linear system of second-order boundary value problems, Computers & Mathematics with Applications, 2009, 57, 757-762. doi: 10.3969/j.issn.1001-3695.2009.02.108 [7] F. Geng and M. Cui, A reproducing kernel method for solving nonlocal fractional boundary value problems, Applied Mathematics Letters, 2012, 25, 818-823. doi: 10.1016/j.aml.2011.10.025 [8] Y. Gupta and M. Kumar, B-Spline Based Numerical Algorithm for Singularly Perturbed Problem of Fourth Order, American Journal of Computational and Applied Mathematics, 2012, 2, 29-32. doi: 10.5923/j.ajcam.20120202.06 [9] M. S. Hashemi, Invariant subspaces admitted by fractional differential equations with conformable derivatives, Chaos, Solitons & Fractals, 2018, 107, 161-169. [10] L. Huang, X. Li, Y. Zhao and X. Duan, Approximate solution of fractional integro-differential equations by Taylor expansion method, Computers & Mathematics with Applications, 2011, 62, 1127-1134. [11] M. Ilie, J. Biazar and Z. Ayati, The first integral method for solving some conformable fractional differential equations, Optical and Quantum Electronics, 2018, 50, 55. doi: 10.1007/s11082-017-1307-x [12] B. Inan, M. S. Osman, T. Ak and D. Baleanu, Analytical and numerical solutions of mathematical biology models: The Newell-Whitehead-Segel and Allen-Cahn equations, Mathematical Methods in the Applied Sciences, 2020, 43, 2588-2600. doi: 10.1002/mma.6067 [13] A. Kilbas, H. Srivastava and J. Trujillo, Theory and Applications of Fractional Differential Equations, Elsevier, Netherlands, 2006. [14] S. Kumar, A. Kumar, B. Samet, J. F. Gómez-Aguilar and M. S. Osman, A chaos study of tumor and effector cells in fractional tumor-immune model for cancer treatment, Chaos, Solitons & Fractals, 2020, 141, 110321 [15] S. Kumar, R. Kumar, M. S. Osman and B. Samet, A wavelet based numerical scheme for fractional order SEIR epidemic of measles by using Genocchi polynomials, 2021, 37, 1250-1268. [16] M. K. Kadalbajoo and V. Kumar, B-spline method for a class of singular two-point boundary value problems using optimal grid, Applied Mathematics and Computation, 2007, 188, 1856-1869. doi: 10.1016/j.amc.2006.11.050 [17] A. Khalid, A. S. A. Alsubaie, M. Inc, A. Rehan, W. Mahmoud and M. S. Osman, Cubic splines solutions of the higher order boundary value problems arise in sandwich panel theory, Results in Physics, 2022, 39, 105726. doi: 10.1016/j.rinp.2022.105726 [18] R. Khalil, M. Al Horani, A. Yousef and M. Sababheh, A new definition of fractional derivative, Journal of Computational and Applied Mathematics, 2014, 264, 65-70. doi: 10.1016/j.cam.2014.01.002 [19] T. U. Khan and M. A. Khan, Generalized conformable fractional operators, Journal of Computational and Applied Mathematics, 2019, 346, 378-389 doi: 10.1016/j.cam.2018.07.018 [20] S. Liu, W. Jiang, X. Li and X. Zhou, Lyapunov stability analysis of fractional nonlinear systems, Applied Mathematics Letters, 2016, 51, 13-19. doi: 10.1016/j.aml.2015.06.018 [21] M. Lakestania and M. Dehghan, Four techniques based on the B-spline expansion and the collocation approach for the numerical solution of the Lane-Emden equation, Mathemathical Methods in Applied Sciences, 2013, 36, 2243-2253. doi: 10.1002/mma.2755 [22] B. Latif, S. A. A. Karim and I. Hashim, New Cubic B-Spline Approximation for Solving Linear Two-Point Boundary-Value Problems, Mathematics, 2021, 9, 1250. doi: 10.3390/math9111250 [23] F. Mainardi, Fractional Calculus and Waves in Linear Viscoelasticity, Imperial College Press, UK, 2010. [24] F. Pitolli, A Fractional B-spline collocation method for the numerical solution of fractional Predator-Prey models, Fractal Fractional, 2018, 2, 13. doi: 10.3390/fractalfract2010013 [25] I. Podlubny, Fractional Differential Equations, Academic Press, USA, 1999. [26] P. Roul and V. M. K. P. Goura, B-spline collocation methods and their convergence for a class of nonlinear derivative dependent singular boundary value problems, Applied Mathematics and Computation, 2019, 341, 428-450. doi: 10.1016/j.amc.2018.09.011 [27] H. Rezazadeh, S. M. M. Alizamini, M. Eslami, M. Rezazadeh, M. Mirzazadeh and S. Abbagari, New optical solitons of nonlinear conformable fractional Schrpodinger-Hirota equation, Optik, 2018, 172, 545-553. doi: 10.1016/j.ijleo.2018.06.111 [28] S. Rashid, K. TulKubra, S. Sultana, P. Agarwal and M. S. Osman, An approximate analytical view of physical and biological models in the setting of Caputo operator via Elzaki transform decomposition method, Journal of Computational and Applied Mathematics, 2022, 413, 114378. doi: 10.1016/j.cam.2022.114378 [29] H. Rezazadeh, H. Tariq, M. Eslami, M. Mirzazadeh and Q. Zhou, New exact solutions of nonlinear conformable time-fractional Phi-4 equation, Chinese Journal of Physics, 2018, 56, 2805-2816. doi: 10.1016/j.cjph.2018.08.001 [30] S. G. Samko, A. A. Kilbas and O. I. Marichev, Fractional Integrals and Derivatives Theory and Applications, Gordon and Breach, USA, 1993. [31] K. Shah, A. Ali and R. A. Khan, Degree theory and existence of positive solutions to coupled systems of multipoint boundary value problems, Boundary Value Problems, 2016, 43. [32] J. Tariboon and S. K. Ntouyas, Oscillation of impulsive conformable fractional differential equations, Open Mathematics, 2016, 14, 497-508. doi: 10.1515/math-2016-0044 [33] G. M. Zaslavsky, Hamiltonian Chaos and Fractional Dynamics, Oxford University Press, UK, 2005. [34] D. Zhao and M. Luo, General conformable fractional derivative and its physical interpretation, Calcolo, 2017, 53, 903-917. -
-
Figures(4) / Tables(10)
Export File
Citation
Ahlem BenRabah, Omar Abu Arqub. AN EFFECTIVE SUSTAINABLE COLLOCATION METHOD FOR SOLVING REGULAR/SINGULAR SYSTEMS OF CONFORMABLE DIFFERENTIAL EQUATIONS SUBJECT TO INITIAL CONSTRAINT CONDITIONS[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1336-1358. doi: 10.11948/20220138
Format
Content
DownLoad:
-
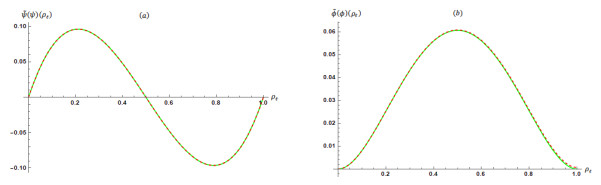
Figure 1.
Results in Problem 1 when
$ m\mathrm{=50} $ $ \psi \left({\rho }_t\right) $ $ \widetilde{\psi }\left({\rho }_t\right) $ -
Figure 2.
Results in Problem 1 when
$ m\mathrm{=40} $ $ E_{\psi }\left({\rho }_t\right) $ $ E_{\phi }\left({\rho }_t\right) $ -
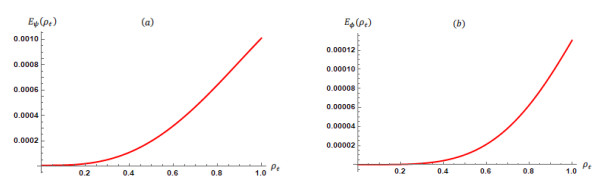
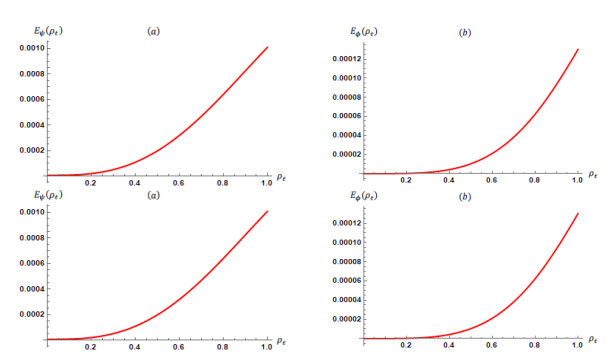
Figure 3.
Results in Problem 3: (a)
$ E_{\psi }\left({\rho }_t\right) $ $ m\mathrm{=100} $ $ E_{\phi }\left({\rho }_t\right) $ $ m\mathrm{=100} $ $ E_{\psi }\left({\rho }_t\right) $ $ m\mathrm{=200} $ $ E_{\phi }\left({\rho }_t\right) $ $ m\mathrm{=200} $ -
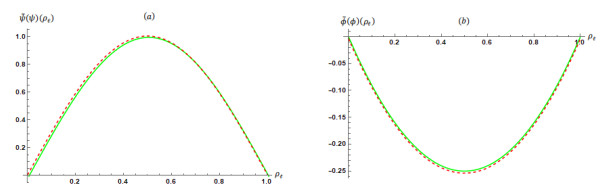
Figure 4.
Results in Problem 4 when
$ m\mathrm{=20} $ $ \psi \left({\rho }_t\right) $ $ \widetilde{\psi }\left({\rho }_t\right) $