| Citation: | Ritu Nigam, Kapil Kant, BV Rathish Kumar, Gnaneshwar Nelakanti. APPROXIMATION OF WEAKLY SINGULAR NON-LINEAR VOLTERRA-URYSOHN INTEGRAL EQUATIONS BY PIECEWISE POLYNOMIAL PROJECTION METHODS BASED ON GRADED MESH[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1359-1387. doi: 10.11948/20220147 |
APPROXIMATION OF WEAKLY SINGULAR NON-LINEAR VOLTERRA-URYSOHN INTEGRAL EQUATIONS BY PIECEWISE POLYNOMIAL PROJECTION METHODS BASED ON GRADED MESH
-
Abstract
In this article, we address the approximation solution of Volterra-Urysohn integral equations which involves weakly singular kernels. In order to get better convergence rates, projection methods namely Galerkin and multi Galerkin methods, along with their iterated versions are used in the space of piecewise polynomials subspaces based on the graded mesh. In addition, we compute the superconvergence results for the proposed integral equation and show that iterated Galerkin method outperforms Galerkin method in terms of order of convergence. Further, we demonstrate numerical examples to verify the proposed theoretical framework.
-

-
References
[1] M. Ahues, A. Largillier and B. Limaye, Spectral computations for bounded operators, Chapman and Hall/CRC, 2001. [2] P. De Angelis, R. De Marchis and A. L. Martire, A new numerical method for a class of Volterra and Fredholm integral equations, J. Comput. Appl. Math., 2020, 379, 112944. doi: 10.1016/j.cam.2020.112944 [3] P. Baratella, A Nyström interpolant for some weakly singular nonlinear Volterra integral equations, J. Comput. Appl. Math., 2013 237(1), 542-555. doi: 10.1016/j.cam.2012.06.024 [4] S. Bazm, P. Lima and S. Nemati, Analysis of the Euler and trapezoidal discretization methods for the numerical solution of nonlinear functional Volterra integral equations of Urysohn type, J. Comput. Appl. Math., 2021, 398, 113628. doi: 10.1016/j.cam.2021.113628 [5] H. Brunner, Collocation methods for Volterra integral and related functional differential equations, Cambridge university press, 2004, 15. [6] H. Brunner, Nonpolynomial spline collocation for Volterra equations with weakly singular kernels, SIAM J. Numer. Anal., 1983, 20(6), 1106-1119. doi: 10.1137/0720080 [7] H. Brunner, The approximate solution of Volterra equations with nonsmooth solutions, Util. Math., 1985, 27, 57-95. [8] H. Brunner, The numerical solution of weakly singular Volterra integral equations by collocation on graded meshes, Math. Comput., 1985, 45(172), 417-437. doi: 10.1090/S0025-5718-1985-0804933-3 [9] H. Brunner, A. Pedas and G. Vainikko, The piecewise polynomial collocation method for nonlinear weakly singular Volterra equations, Math. Comput., 1999, 68(227), 1079-1095. doi: 10.1090/S0025-5718-99-01073-X [10] Z. Chen, G. Long and G. Nelakanti, The discrete multi-projection method for Fredholm integral equations of the second kind, J. Integral Equations Appl., 2007, 19(2), 143-162. [11] N. M. Darani, K. Maleknejad and H. Mesgarani, A new approach for two-dimensional nonlinear mixed Volterra-Fredholm integral equations and its convergence analysis, TWMS J. Pure Appl. Math., 2019, 10(1), 132-139. [12] I. G. Graham, Galerkin methods for second kind integral equations with singularities, Math. Comput., 1982, 39(160), 519-533. doi: 10.1090/S0025-5718-1982-0669644-3 [13] F. de Hoog and R. Weiss, On the solution of a Volterra integral equation with a weakly singular kernel, SIAM J. Numer. Anal., 1973, 4(4), 561-573. doi: 10.1137/0504049 [14] H. Kaneko, R. D. Noren and Y. Xu, Numerical solutions for weakly singular Hammerstein equations and their superconvergence, J. Integral Equations Appl., 1992, 4(3), 391-407. [15] R. Katani, A Numerical Method for Proportional Delay Volterra Integral Equations, Int. J. Appl. Comput. Math., 2021, 7(4), 1-13. [16] R. Karim and A. AL-Rammahi, q-homotopy analysis method for solving nonlinear Fredholm integral equation of the second kind, Int. J. Nonlinear Anal. Appl., 2021, 12(2), 2145-2152. [17] M. Kazemi, V. Torkashvand and E. Fathizade, A new iterative method of successive approximation to solve nonlinear Urysohn integral equations by Haar wavelet, International Journal of Mathematical Modelling and Computations, 2020, 10(4 (Fall)), 281-294. [18] K. Kant and G. Nelakanti, Galerkin and multi-Galerkin methods for weakly singular Volterra–Hammerstein integral equations and their convergence analysis, Computat. Appl. Math., 2020, 39(2), 1-28. [19] C. Lubich, Runge-Kutta theory for Volterra and Abel integral equations of the second kind, Math. Comput., 1983, 41(163), 87-102. doi: 10.1090/S0025-5718-1983-0701626-6 [20] M. Mandal and G. Nelakanti, Superconvergence Results for Volterra-Urysohn Integral Equations of Second Kind, ICMC, 2017, 655, 358-379. [21] W. R. Mann and F. Wolf, Heat transfer between solids and gases under nonlinear boundary conditions, Q. Appl. Math., 1951, 9(2), 163-184. doi: 10.1090/qam/42596 [22] S. Micula, A numerical method for weakly singular nonlinear Volterra integral equations of the second kind, Symmetry, 2020, 12(11), 1862. doi: 10.3390/sym12111862 [23] R. K. Miller and A. Feldstein, Smoothness of solutions of Volterra integral equations with weakly singular kernels, SIAM J. Math. Anal., 1971, 2(2), 242-258. doi: 10.1137/0502022 [24] W. E. Olmstead and R. A. Handelsman, Diffusion in a semi-infinite region with nonlinear surface dissipation, SIAM review, 1976, 18(2), 275-291. doi: 10.1137/1018044 [25] D. O'regan, Volterra and Urysohn integral equations in Banach spaces, J. Appl. Math. Stoch. Anal., 1998, 11(4), 449-464. doi: 10.1155/S1048953398000379 [26] A. Orsi, Product integration for Volterra integral equations of the second kind with weakly singular kernels, Math. Comput., 1996, 65(215), 1201-1212. doi: 10.1090/S0025-5718-96-00736-3 [27] C. Pozrikidis, The Numerical Solution of Integral Equations of the Second Kind, J. Fluid Mech., 1998, 372, 375-378. [28] M. Rebelo and T. Diogo, A hybrid collocation method for a nonlinear Volterra integral equation with weakly singular kernel, J. Comput. Appl. Math., 2010, 234(9), 2859-2869. doi: 10.1016/j.cam.2010.01.034 [29] L. Schumaker, Spline functions: basic theory, Cambridge University Press, 2007. [30] S. Sohrabi, H. Ranjbar and M. Saei, Convergence analysis of the Jacobi-collocation method for nonlinear weakly singular Volterra integral equations, Appl. Math. Comput., 2017, 299, 141-152. [31] T. Tang, X. Xu and J. Cheng, On spectral methods for Volterra integral equations and the convergence analysis, J. Comput. Math., 2008 26(6), 825-837. [32] L. Tao and H. Yong, Extrapolation method for solving weakly singular nonlinear Volterra integral equations of the second kind, J. Math. Anal. Appl., 2006, 324(1), 225-237. doi: 10.1016/j.jmaa.2005.12.013 [33] G. M. Vainikko, Galerkin's perturbation method and the general theory of approximate methods for non-linear equations, Comput. Math. Math., 1967, 7(4), 1-41. doi: 10.1016/0041-5553(67)90140-1 [34] Z. Xie, X. Li and T. Tang, Convergence analysis of spectral Galerkin methods for Volterra type integral equations, J. Sci. Comput., 2012, 53(2), 414-434. doi: 10.1007/s10915-012-9577-8 [35] M. A. Zaky and I. G. Ameen, A novel Jacob spectral method for multi-dimensional weakly singular nonlinear Volterra integral equations with nonsmooth solutions, Eng. Comput., 2021, 37(4), 2623-2631. doi: 10.1007/s00366-020-00953-9 -
-
-
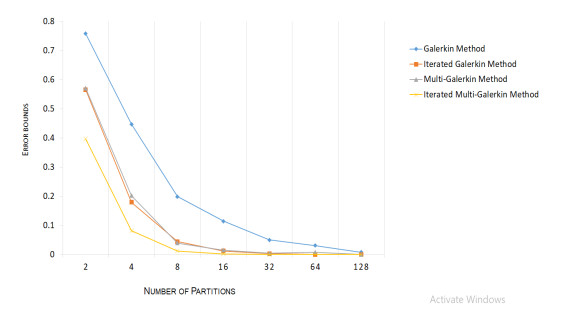
Figure 1.
Comparison of error bounds among all the proposed methods
-
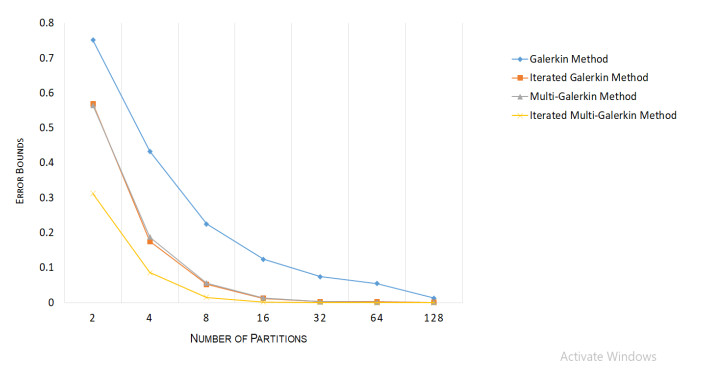
Figure 2.
Comparison of error bounds among all the proposed methods




 DownLoad:
DownLoad: