| Citation: |
Xiaoxue Zhang, Chuanjian Wang, Changzhao Li, Lirong Wang. DEGENERATION OF LUMP-TYPE LOCALIZED WAVES IN THE (2+1)-DIMENSIONAL ITO EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1090-1103. doi: 10.11948/20220137
|
DEGENERATION OF LUMP-TYPE LOCALIZED WAVES IN THE (2+1)-DIMENSIONAL ITO EQUATION
-
Abstract
The degeneration of lump-type localized waves in the (2+1)-dimen-sional Ito equation is investigated through the parallel relationship of wave numbers. These lump-type localized waves can degenerate into three different kinds of localized wave solutions: singular lump-type localized wave, periodic variable amplitude localized wave, rogue wave. In the process of propagation, the lump-type localized waves keep the same waveform structure and amplitude. However, the periodic variable amplitude localized wave demonstrates three different kinds of waveform structures, which presents an interesting emit-absorb interaction phenomenon. By an emitting and absorbing interaction, the localized wave realizes the energy exchange from one localized wave to another, and keeps the original waveform structure. Rogue wave is a rational growing-and-decaying localized wave which is localized in both space and time.
-
Keywords:
- (2+1)-dimensional Ito equation /
- lump-type localized wave /
- degeneration /
- rogue wave
-
-
References
[1] A. R. Adem, The generalized (1+1)-dimensional and (2+1)-dimensional Ito equations: Multiple exp-function algorithm and multiple wave solutions, Comput. Math. Appl., 2016, 71(6), 1248–1258. doi: 10.1016/j.camwa.2016.02.005 [2] S. Bhatter, A. Mathur, D. Kumar et al., A new analysis of fractional DrinfeldSokolov-Wilson model with exponential memory, Physica A, 2020, 537, 122578. doi: 10.1016/j.physa.2019.122578 [3] S. Chen and X. Lü, Lump and lump-multi-kink solutions in the (3+1)- dimensions, Commun. Nonlinear. Sci. Numer. Simul., 2022, 109, 106103. doi: 10.1016/j.cnsns.2021.106103 [4] S. Chen, X. Lü et al., Derivation and simulation of the M-lump solutions to two (2+1)-dimensional nonlinear equations, Phys. Scr., 2021, 96(9), 095201. doi: 10.1088/1402-4896/abf307 [5] A. Chabchoub, N. P. Hoffmann and N. Akhmediev, Rogue Wave Observation in a Water Wave Tank, Phys. Rev. Lett., 2011, 106(20), 204502. doi: 10.1103/PhysRevLett.106.204502 [6] Y. Feng, B. Sudao and X. Wang, Diverse exact analytical solutions and novel interaction solutions for the (2+ 1)-dimensional Ito equation, Phys. Scr., 2020, 95(9), 095201. doi: 10.1088/1402-4896/aba71b [7] M. Gürses, A. Karasu and V. V. Sokolov, On construction of recursion operators from Lax representation, J. Math. Phys., 1999, 40(12), 6473–6490. doi: 10.1063/1.533102 [8] C. He, Y. Tang, W. Ma and J. Ma, Interaction phenomena between a lump and other multi-solitons for the (2+1)-dimensional BLMP and Ito equations, Nonlinear Dyn., 2019, 95(1), 29–42. doi: 10.1007/s11071-018-4548-8 [9] R. Hirota, The direct method in soliton theory, Cambridge University Press, Cambridge, UK, 2004. [10] M. Ito, An extension of nonlinear evolution equations of the KdV (mKdV) type to higher orders, J. Phys. Soc. Jpn., 1980, 49(2), 771–778. doi: 10.1143/JPSJ.49.771 [11] X. Lü and S. Chen, New general interaction solutions to the KPI equation via an optional decoupling condition approach, Commun. Nonlinear. Sci. Numer. Simul., 2021, 103, 105939. doi: 10.1016/j.cnsns.2021.105939 [12] X. Lü and S. Chen, Interaction solutions to nonlinear partial differential equations via Hirota bilinear forms: one-lump-multi-stripe and one-lump-multisoliton types, Nonlinear Dyn., 2021, 103(1), 947–977. doi: 10.1007/s11071-020-06068-6 [13] X. Lü, Y. Hua et al., Integrability characteristics of a novel (2+1)-dimensional nonlinear model: Painlevé analysis, soliton solutions, Bäcklund transformation, Lax pair and infinitely many conservation laws, Commun. Nonlinear. Sci. Numer. Simul., 2021, 95, 105612. doi: 10.1016/j.cnsns.2020.105612 [14] Q. Liu, Hamiltonian structures for Ito's equation, Phys. Lett. A, 2000, 277(1), 31–34. doi: 10.1016/S0375-9601(00)00684-8 [15] D. Li and J. Zhao, New exact solutions to the (2+1)-dimensional Ito equation: Extended homoclinic test technique, Appl. Math. Comput., 2009, 215(5), 1968– 1974. [16] W. Ma, X. Yong and H. Zhang, Diversity of interaction solutions to the (2+1)- dimensional Ito equation, Comput. Math. Appl., 2018, 75(1), 289–295. doi: 10.1016/j.camwa.2017.09.013 [17] H. Ma, H. Wu, W. Ma and A. Deng, Localized interaction solutions of the (2+1)-dimensional Ito Equation, Opt. Quantum Electron., 2021, 53(6), 1–16. [18] S. Tian and H. Zhang, Riemann theta functions periodic wave solutions and rational characteristics for the (1+1)-dimensional and (2+1)-dimensional Ito equation, Chaos Solitons Fractals, 2013, 47, 27–41. doi: 10.1016/j.chaos.2012.12.004 [19] Y. Tian and Z. Dai, Rogue waves and new multi-wave solutions of the (2+1)- dimensional Ito equation, Z. Naturforsch. A, 2013, 70(6), 437–443. [20] W. Tan, Z. Dai and H. Dai, Dynamical analysis of lump solution for the (2+1)- dimensional Ito equation, Therm. Sci., 2017, 21(4), 1673–1679. doi: 10.2298/TSCI160812145T [21] W. Tan, Some new dynamical behaviour of double breathers and lump-Nsolitons for the Ito equation, Int. J Comput. Math., 2021, 98(5), 961–974. doi: 10.1080/00207160.2020.1792454 [22] X. Tan and Q. Zha, Three wave mixing effect in the (2+1)-dimensional Ito equation, Int. J Comput. Math., 2021, 98(10), 1921–1934. doi: 10.1080/00207160.2020.1867116 [23] W. Tan, W. Zhang and J. Zhang, Evolutionary behavior of breathers and interaction solutions with M-solitons for (2+1)-dimensional KdV system, Appl. Math. Lett., 2020, 101, 106063. doi: 10.1016/j.aml.2019.106063 [24] A. M. Wazwaz, Multiple-soliton solutions for the generalized (1+1)-dimensional and the generalized (2+1)-dimensional Ito equations, Appl. Math. Comput., 2008, 202(2), 840–849. [25] X. Wang, S. Tian, C. Qin and T. Zhang, Dynamics of the breathers, rogue waves and solitary waves in the (2+1)-dimensional Ito equation, Appl. Math. Lett., 2017, 68, 40–47. doi: 10.1016/j.aml.2016.12.009 [26] L. Wang, C. Liu, M. Li et al., High-dimensional nonlinear wave transitions and their mechanism, Chaos, 2020, 30(11), 113107. doi: 10.1063/5.0019596 [27] C. Wang, Spatiotemporal deformation of lump solution to (2+1)-dimensional KdV equation, Nonlinear Dyn., 2016, 84(2), 697–702. doi: 10.1007/s11071-015-2519-x [28] C. Wang, H. Fang and X. Tang, State transition of lump-type waves for the (2+1)-dimensional generalized KdV equation, Nonlinear Dyn., 2019, 95(4), 2943–2961. doi: 10.1007/s11071-018-04733-5 [29] C. Wang, Z. Dai and C. Liu, Interaction Between Kink Solitary Wave and Rogue Wave for (2+1)-Dimensional Burgers Equation, Mediterr. J. Math., 2016, 13(3), 1087–1098. doi: 10.1007/s00009-015-0528-0 [30] J. Yang, W. Ma and Z. Qin, Lump and lump-soliton solutions to the (2+1)- dimensional Ito equation, Anal. Math. Phys., 2018, 8(3), 427–436. doi: 10.1007/s13324-017-0181-9 [31] Y. Zhang and D. Chen, N-soliton-like solution of Ito equation, Commun. Theor. Phys., 2004, 42(5), 641–644. doi: 10.1088/0253-6102/42/5/641 [32] Z. Zhao, Y. Zhang and Z. Han, Symmetry analysis and conservation laws of the Drinfeld-Sokolov-Wilson system, Eur. Phys. J. Plus, 2014, 129(7), 143. doi: 10.1140/epjp/i2014-14143-x [33] Y. Zhang, Y. You, W. Ma and H. Zhao, Resonance of solitons in a coupled higher-order Ito equation, J. Math. Anal. Appl., 2012, 394(1), 121–128. doi: 10.1016/j.jmaa.2012.03.030 [34] X. Zhang, C. Wang and Y. Zhou, High-order localized waves in the (2+1)- dimensional Ito equation, Phys. Scr., 2021, 96(7), 075215. doi: 10.1088/1402-4896/abfcf0 -
-
Figures(7)
Export File
Citation
Xiaoxue Zhang, Chuanjian Wang, Changzhao Li, Lirong Wang. DEGENERATION OF LUMP-TYPE LOCALIZED WAVES IN THE (2+1)-DIMENSIONAL ITO EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1090-1103. doi: 10.11948/20220137
Format
Content
DownLoad:
-
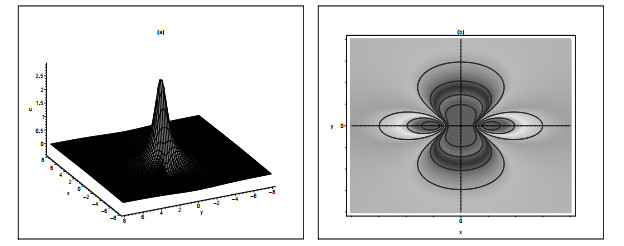
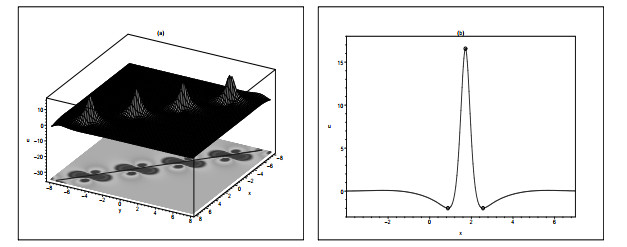
Figure 1. (a) The spatial localized structure and periodic features of the lump-type localized wave chain. (b) Sectional view in period unit showing peak and two troughs. The parameter values are
$ (\alpha,\beta,\gamma,a_1,b_1,d_1,l_1)=(1,1,1,1,1,1.5,-3) $ . -
Figure 2. (a) The spatial structure structure of the singular lump-type localized wave. (b) Contour plot showing its symmetry. The parameter values are
$ (\alpha,\beta,\gamma,a_1,b_1,d_1,l_1)=(1,1,\frac{5}{8},1,1,1.5,-3) $ . -
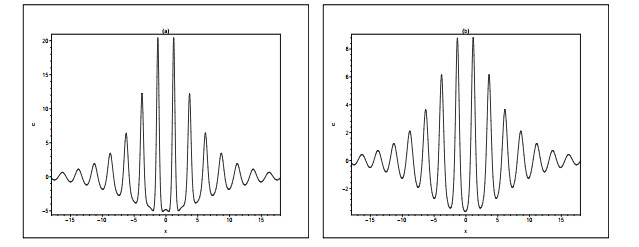
Figure 3. The waveform structures of solution (3.6) at different points of time in one period. From left to right, the point in time takes
$ t=-1, -0.4, -0.1, 0.3 , 0.8 $ , respectively. The parameter values are$ (\alpha,\beta,b_1,d_1,a_1,l_1)=(1,1,1,1,2,-3) $ . -
Figure 4. The waveform structures of solution (3.6) at different points of time in one period. From right to left, the point in time takes
$ t=-0.8, -0.2, -0.07, 0.1 , 0.63 $ , respectively. The parameter values are$ (\alpha,\beta,b_1,d_1,a_1,l_1)=(1,1,1,1,1,-3) $ . -
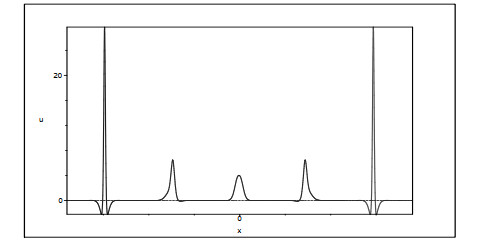
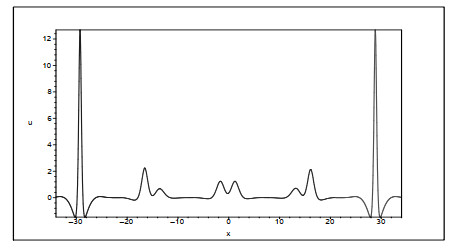
Figure 5. The oscillation phenomena of localized wave: (a)
$ \delta<0 $ ; (b)$ \delta>0 $ . The parameter values are$ (\alpha,\beta,d_1, a_1,b_1,l_1 )=(1,1,1,0.2, 2.5,-0.15) $ and$ (\alpha,\beta,d_1, a_1,b_1,l_1 )=(1,1,1,0.2, 2.5,-0.3) $ , respectively. -
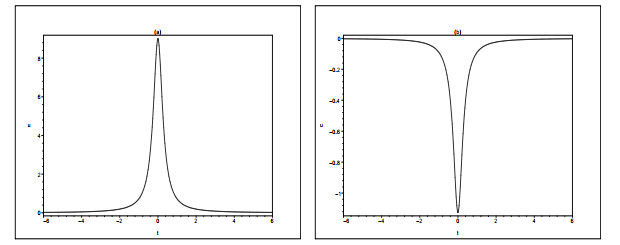
Figure 6. The time evolution plots of the maximum and minimum values: (a)
$ u_{max}(t) $ and (b)$ u_{min}(t) $ . The parameter values are$ (\alpha,\beta,a_1,b_1,d_1,l_1)=(1,1,1,1,1.5,-3) $ . -
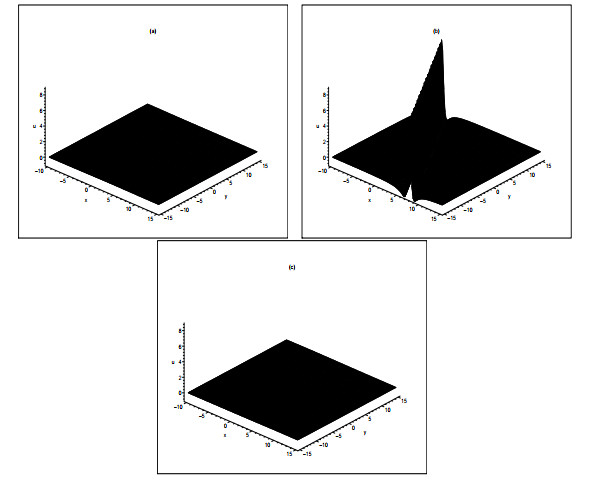
Figure 7. The spatiotemporal evolution plots of the solution (3.10): (a)
$ t=-5 $ , (b)$ t=0 $ and (c)$ t=5 $ . The parameter values are$ (\alpha,\beta,a_1,b_1,d_1,l_1)=(1,1,1,1,1.5,-3) $ .