| Citation: |
Jiazhe Lin, Ling Zhou, Zhu Zhou. FIXED-TIME SYNCHRONIZATION OF A REACTION-DIFFUSION BAM NEURAL NETWORK WITH DISTRIBUTED DELAY AND ITS APPLICATION TO IMAGE ENCRYPTION[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 1869-1892. doi: 10.11948/20220300
|
FIXED-TIME SYNCHRONIZATION OF A REACTION-DIFFUSION BAM NEURAL NETWORK WITH DISTRIBUTED DELAY AND ITS APPLICATION TO IMAGE ENCRYPTION
-
Abstract
In this paper, we investigate the fixed-time synchronization of reaction-diffusion BAM neural networks, where both discrete and distributed delays are taken into account. Combining Lyapunov stability theory and several integral inequalities, fixed-time synchronization criteria of master and slave systems are established. Through sensitivity analysis, we find the key controller parameters that have a great influence on the maximum settling time. Using the chaotic sequences generated by the neural network, the color image can be encrypted by the Arnold Cat Map and pixel diffusion. Experiments show that the image encryption algorithm designed in this paper has excellent properties of security and anti-attacking, which meets the requirements for the secure transmission of image information.
-
-
References
[1] H. Bao and J. Cao, Exponential stability for stochastic BAM networks with discrete and distributed delays, Applied Mathematics and Computation, 2012, 218(11), 6188-6199. doi: 10.1016/j.amc.2011.11.035 [2] N. Bigdeli, Y. Farid and K. Afshar, A novel image encryption/decryption scheme based on chaotic neural networks, Engineering Applications of Artificial Intelligence, 2012, 25(4), 753-765. doi: 10.1016/j.engappai.2012.01.007 [3] D. Breda and S. D. Schiava, Pseudospectral reduction to compute Lyapunov exponents of delay differential equations, Discrete and Continuous Dynamical Systems Series B, 2018, 23(7), 2727-2741. doi: 10.3934/dcdsb.2018092 [4] C. Chen, L. Li, H. Peng and Y. Yang, Fixed-time synchronization of memristor-based BAM neural networks with time-varying discrete delay, Neural Networks, 2017, 96, 47-54. doi: 10.1016/j.neunet.2017.08.012 [5] W. Chen, S. Luo and W. X. Zheng, Impulsive synchronization of reaction-diffusion neural networks with mixed delays and its application to image encryption, IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(12), 2696-2710. doi: 10.1109/TNNLS.2015.2512849 [6] M. Garvie, Finite-difference schemes for reaction-diffusion equations modeling predator-prey interactions in MATLAB, Bulletin of Mathematical Biology, 2007, 69(3), 931-956. doi: 10.1007/s11538-006-9062-3 [7] K. Gu, An integral inequality in the stability problem of time-delay systems, Proceedings of the 39th IEEE Conference on Decision and Control, 2000, 3, 2805-2810. [8] Y. Guo, Y. Luo, W. Wang, et al., Fixed-time synchronization of complex-valued memristive BAM neural network and applications in image encryption and decryption, International Journal of Control, Automation and Systems, 2020, 18(2), 462-476. doi: 10.1007/s12555-018-0676-7 [9] C. Han, An image encryption algorithm based on modified logistic chaotic map, Optik, 2019, 181, 779-785. doi: 10.1016/j.ijleo.2018.12.178 [10] G. Hardy, J. Littlewood and G. Polya, Inequalities, Cambridge University Press, Cambridge, 1952. [11] Y. He, Y. Zhang and X. Wang, A new image encryption algorithm based on two-dimensional spatiotemporal chaotic system, Neural Computing and Applications, 2018, 32(1), 247-260. [12] Y. He, Y. Zhang and X. Wang, A new image encryption algorithm based on two-dimensional spatiotemporal chaotic system, Neural Computing and Applications, 2020, 32, 247-260. doi: 10.1007/s00521-018-3577-z [13] E. Karaoğlu, E. Yılmaz and H. Merdan, Stability and bifurcation analysis of two-neuron network with discrete and distributed delays, Neurocomputing, 2016, 182, 102-110. doi: 10.1016/j.neucom.2015.12.006 [14] S. Karthick, R. Sakthivel, C. Wang and Y.-K. Ma, Synchronization of coupled memristive neural networks with actuator saturation and switching topology, Neurocomputing, 2020, 383, 138-150. doi: 10.1016/j.neucom.2019.11.034 [15] B. Kosko, Adaptive bidirectional associative memories, Applied Optics, 1987, 26(23), 4947-4960. doi: 10.1364/AO.26.004947 [16] R. Li, J. Cao, A. Alsaedi and F. Alsaadi, Exponential and fixed-time synchronization of Cohen-Grossberg neural networks with time-varying delays and reaction-diffusion terms, Applied Mathematics and Computation, 2017, 313, 37-51. doi: 10.1016/j.amc.2017.05.073 [17] X. Li, J. Fang, W. Zhang and H. Li, Finite-time synchronization of fractional-order memristive recurrent neural networks with discontinuous activation functions, Neurocomputing, 2018, 316, 284-293. doi: 10.1016/j.neucom.2018.08.003 [18] H. Liu, X. Wang and A. Kadir, Chaos-based color image encryption using one-time keys and choquet fuzzy integral, International Journal of Nonlinear Sciences and Numerical Simulation, 2014, 15(1), 1-10. doi: 10.1515/ijnsns-2011-0001 [19] Z. Liu, L. Xu, T. Liu, et al., Color image encryption by using Arnold transform and color-blend operation in discrete cosine transform domains, Optics Communications, 2011, 284(1), 123-128. doi: 10.1016/j.optcom.2010.09.013 [20] J. {Lu}, Robust global exponential stability for interval reaction-diffusion Hopfield neural networks with distributed delays, IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2007, 54(12), 1115-1119. doi: 10.1109/TCSII.2007.905357 [21] J. Lu, Global exponential stability and periodicity of reaction-diffusion delayed recurrent neural networks with Dirichlet boundary conditions, Chaos, Solitons and Fractals, 2008, 35(1), 116-125. doi: 10.1016/j.chaos.2007.05.002 [22] A. Luo, A theory for synchronization of dynamical systems, Communications in Nonlinear Science and Numerical Simulation, 2009, 14, 1901-1951. doi: 10.1016/j.cnsns.2008.07.002 [23] S. Marino, I. B. Hogue, C. J. Ray and D. E. Kirschner, A methodology for performing global uncertainty and sensitivity analysis in systems biology, Journal of Theoretical Biology, 2008, 254(1), 178-196. doi: 10.1016/j.jtbi.2008.04.011 [24] I. Nejadgholi, S. Seyyedsalehi and S. Chartier, A chaotic feature extracting BAM and its application in implementing memory search, Neural Processing Letters, 2012, 36(1), 69-99. doi: 10.1007/s11063-012-9223-3 [25] A. Polyakov, Nonlinear feedback design for fixed-time stabilization of linear control systems, IEEE Transactions on Automatic Control, 2012, 57, 2106-2110. doi: 10.1109/TAC.2011.2179869 [26] X. Qin, C. Wang, L. Li, et al., Finite-time projective synchronization of memristor-based neural networks with leakage and time-varying delays, Physica A: Statistical Mechanics and its Applications, 2019, 531, 121788. doi: 10.1016/j.physa.2019.121788 [27] A. Saltelli, Sensitivity analysis for importance assessment, Risk analysis, 2002, 22(3), 579-590. doi: 10.1111/0272-4332.00040 [28] P. Selvaraj, R. Sakthivel and O. Kwon, Finite-time synchronization of stochastic coupled neural networks subject to markovian switching and input saturation, Neural Networks, 2018, 105, 154-165. doi: 10.1016/j.neunet.2018.05.004 [29] X. Wang and Z. Li, A color image encryption algorithm based on Hopfield chaotic neural network, Optics and Lasers in Engineering, 2019, 115, 107-118. doi: 10.1016/j.optlaseng.2018.11.010 [30] Q. Xiao, Z. Huang and Z. Zeng, Passivity analysis for memristor-based inertial neural networks with discrete and distributed delays, IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019, 49(2), 375-385. [31] J. Yan and J. Shen, Impulsive stabilization of impulsive functional differential equations by Lyapunov-Razumikhin functions, Nonlinear Analysis, 1999, 37, 245-255. doi: 10.1016/S0362-546X(98)00045-5 [32] B. Zhou and Q. Song, Stability and Hopf bifurcation analysis of a tri-neuron BAM neural network with distributed delay, Neurocomputing, 2012, 82, 69-83. doi: 10.1016/j.neucom.2011.10.031 [33] H. Zhu, C. Zhao, X. Zhang and L. Yang, An image encryption scheme using generalized Arnold map and affine cipher, Optik, 2014, 125(22), 6672-6677. doi: 10.1016/j.ijleo.2014.06.149 [34] Z. L. Zhu, W. Zhang, K. Wong and H. Yu, A chaos-based symmetric image encryption scheme using a bit-level permutation, Information Sciences, 2011, 181(6), 1171-1186. doi: 10.1016/j.ins.2010.11.009 -
-
Figures(13)
Export File
Citation
Jiazhe Lin, Ling Zhou, Zhu Zhou. FIXED-TIME SYNCHRONIZATION OF A REACTION-DIFFUSION BAM NEURAL NETWORK WITH DISTRIBUTED DELAY AND ITS APPLICATION TO IMAGE ENCRYPTION[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 1869-1892. doi: 10.11948/20220300
Format
Content
DownLoad:
-
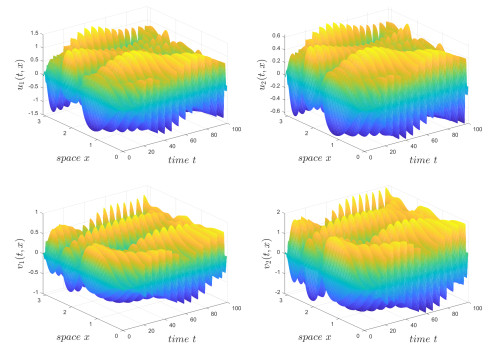
Figure 1.
Spatiotemporal chaos of neuron states
$ u_1(t, x) $ $ u_2(t, x) $ $ v_1(t, x) $ $ v_2(t, x) $ -
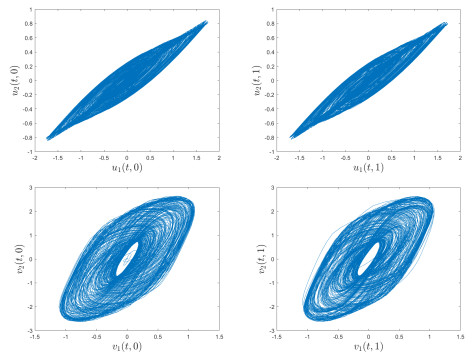
Figure 2.
Phase diagrams of neuronic state variables
$ (u_1(t, 0), u_2(t, 0)) $ $ (u_1(t, 1), u_2(t, 1)) $ $ (v_1(t, 0), v_2(t, 0)) $ $ (v_1(t, 1), v_2(t, 1)) $ -
Figure 3.
Spatiotemporal dynamical behaviors of the corresponding error system.
-
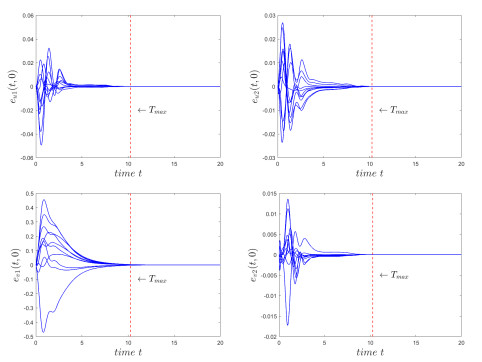
Figure 4.
Synchronization error states
$ e_{u1}(t, 0) $ $ e_{u2}(t, 0) $ $ e_{v1}(t, 0) $ $ e_{v2}(t, 0) $ -
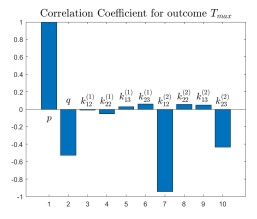
Figure 5.
PRCCs of
$ T_{\max} $ $ p $ $ q $ $ {k_{12}^{(1)}} $ $ {k_{13}^{(1)}} $ $ {k_{22}^{(1)}} $ $ {k_{23}^{(1)}} $ $ {k_{12}^{(2)}} $ $ {k_{13}^{(2)}} $ $ {k_{22}^{(2)}} $ $ {k_{23}^{(2)}} $ -
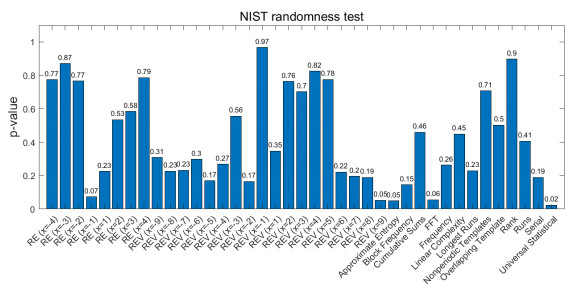
Figure 6.
P-values of NIST randomness test for matrix
$ K $ -
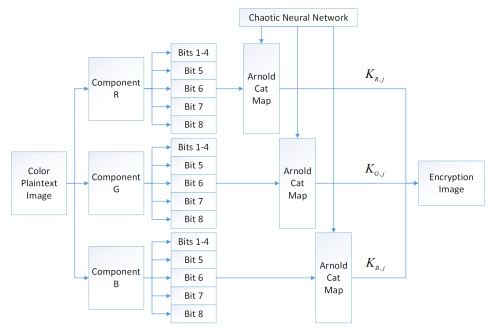
Figure 7.
Block diagram of image encryption algorithm.
-
Figure 8.
Original, encrypted and decrypted images of component R, respectively.
-
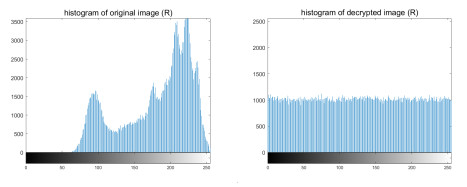
Figure 9.
Histograms of original and decrypted images.
-
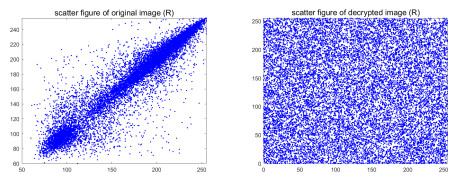
Figure 10.
Scatter figures of original and decrypted images (R) in diagonal direction.
-
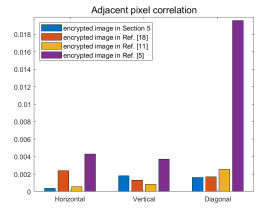
Figure 11.
Adjacent pixel correlation of encrypted images in literature [5, 11] and[18].
-
Figure 12.
Decryption effect under different shear attacks.
-
Figure 13.
Decryption effect under different noise interference.