| Citation: | Qiaoyun Wang, Na Wang, Xianbo Sun. MONOTONICITY OF THE RATIOS OF TWO ABELIAN INTEGRALS FOR HAMILTONIAN SYSTEMS WITH PARAMETERS[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 2466-2487. doi: 10.11948/20220349 |
MONOTONICITY OF THE RATIOS OF TWO ABELIAN INTEGRALS FOR HAMILTONIAN SYSTEMS WITH PARAMETERS
-
Abstract
We study the monotonicity of the ratios of two Abelian integrals $ \oint_{\gamma_{i}(h)}ydx $ $ \backslash $ $ \oint_{\gamma_{i}(h)}xydx $ over three period annuli $ \{\gamma_i(h)\} $, for $ i=1, 2, 3 $, defined by a seventh-degree hyperelliptic Hamiltonian $ H(x, y)=y^2+\Psi(x) $ with a parameter. The parameter makes the problem more challenging to analyze. To overcome the difficulty, we apply some criterion with the help of transformations, tools in computer algebra such as boundary polynomial theory to determine the monotonicity of the ratios. Our results establish the existence and uniqueness of limit cycle bifurcated from each period annulus.
-
Keywords:
- Abelian integral /
- monotonicity /
- Hamiltonian system
-

-
References
[1] V. I. Arnold, Ten Problems, Adv. Soviet. Math., 1990. [2] R. Asheghi and A. Bakhshalizadeh, The Chebyshev's property of certain hyperelliptic integrals of the first kind, Chaos, Solitons and Fractals, 2015, 78, 162–175. doi: 10.1016/j.chaos.2015.07.020 [3] A. Bakhshalizadeh, R. Asheghi and R. Hoseyni, Zeros of hyperelliptic integrals of the first kind for special hyperelliptic Hamiltonians of degree 7, Chaos, Solitons and Fractals, 2017, 103, 279–288. doi: 10.1016/j.chaos.2017.06.021 [4] A. Bakhshalizadeh, R. Asheghi and R. Kazemi, On the monotonicity of the ratio of some hyperelliptic integrals of order 7, Bull. Sci. Math., 2020, 158, 1–24. [5] R. Cheng, Z. Luo and X. Hong, Bifurcations and new traveling wave solutions for the nonlinear dispersion drinfel'd-Sokolov $D(m, n)$ system, J. Nonl. Mod. Anal., 2021, 3(2), 193–207. [6] F. Dumortier and C. Li, Perturbations from an elliptic Hamiltonian of degree four: (Ⅰ) Saddle loop and two saddle cycle, J. Differ. Equat., 2001, 176(1), 114–157. doi: 10.1006/jdeq.2000.3977 [7] F. Dumortier and C. Li, Perturbations from an elliptic Hamiltonian of degree four: (Ⅱ) Cuspidal loop, J. Differ. Equat., 2001, 175(2), 209–243. doi: 10.1006/jdeq.2000.3978 [8] F. Dumortier and C. Li, Perturbations from an elliptic Hamiltonian of degree four: (Ⅲ) Global centre, J. Differ. Equat., 2003, 188(2), 473–511. doi: 10.1016/S0022-0396(02)00110-9 [9] F. Dumortier and C. Li, Perturbations from an elliptic Hamiltonian of degree four: (Ⅳ) Figure eightloop, J. Differ. Equat., 2003, 188(2), 512–514. doi: 10.1016/S0022-0396(02)00111-0 [10] A. Gasull, A. Geyer and V. Mañosa, Persistence of periodic traveling waves and Abelian integrals, J. Differ. Equat., 2021, 293, 48–69. doi: 10.1016/j.jde.2021.05.033 [11] A. Geyer, R. Martins, F. Natali and D. Pelinovsky, Stability of smooth periodic travelling waves in the Camassa–Holm equation, Stud. Appl. Math., 2022, 148(1), 27–61. doi: 10.1111/sapm.12430 [12] M. Grau, F. Mañosas and J. Villadelprat, A Chebyshev criterion for Abelian integrals, Trans. Amer. Math. Soc., 2011, 363(1), 109–129. [13] L. Guo and Y. Zhao, Existence of periodic waves for a perturbed quintic BBM equation, Disc. & Cont. Dynam. Syst., 2020, 40(8), 4689–4703. [14] M. Han and J. Yang, The maximum number of zeros of functions with parameters and application to differential equations, J. Nonl. Model. Anal., 2021, 3(1), 13–34. [15] R. Kazemi, Monotonicity of the ration of two Abelian integrals for a class of symmetric hyperelliptic hamiltonian systems, Bull. Sci. Math., 2018, 8(1), 344–355. [16] C. Li, J. Llibre and Z. Zhang, Abelian integrals of quadratic Hamiltonian vector field with an invariant straight line, Publications Matemàtiques., 1995, 39, 355–366. [17] C. Li and Z. Zhang, A criterion for determining the monotonicity of the ratio of two Abelian integrals, J. Differ. Equat., 1996, 124(2), 407–424. [18] F. Li, et al., Integrability and linearizability of cubic $Z_2$ systems with non-resonant singular points, J. Differ. Equat., 2020, 269(10), 9026–9049. $Z_2$ systems with non-resonant singular points" target="_blank">Google Scholar
[19] F. Li, Y. Wu and P. Yu, Complete classification on center of cubic planar systems symmetric with respect to a straight line, Commun. Nonl. Sci. Numer. Simulat., 2023, 20, 107167. [20] C. Liu, G. Chen and Z. Sun, New criteria for the monotonicity of the ratio of two Abelian integrals, J. Math. Anal. Appl., 2018, 465(1), 220–234. [21] C. Liu and D. Xiao, The monotonicity of the ratio of two Abelian integrals, Trans. Amer. Math. Soc., 2013, 365(10), 5525–5544. [22] Y. Song, J. Shi and H. Wang, Spatiotemporal dynamics of a diffusive consumer-resource model with explicit spatial memory, Studies in Applied Mathematics, 2022, 148(1), 373–395. [23] X. Sun, W. Huang and J. Cai, Coexistence of the solitary and periodic waves in convecting shallow water fluid, Nonl. Anal. (RWA), 2020, 53, 1–17. [24] X. Sun, N. Wang and P. Yu, The monotonicity of ratios of some Abelian integrals, Bull. Sci. Math., 2021, 166, 2–11. [25] N. Wang, D. Xiao and J. Wang, The exact bounds on the number of zeros of complete hyperelliptic integrals of the first kind, J. Differ. Equat., 2013, 254(2), 323–341. [26] N. Wang, D. Xiao and J. Yu, The monotonicity of the ratio of hyperelliptic integrals, Bull. Sci. Math., 2014, 138(7), 805–845. [27] L. Yang, X. Hou and B. Xia, A complete algorithm for automated discovering of a class of inequalitytype theorems, Sci. China, Ser. F., 2001, 44(1), 33–49. [28] L. Yang and B. Xia, Real solution classification for parametric semi-algebraic systems, Algorithmic Algebra and Logic, 2005, 281–289. [29] Y. Zhou and J. Zhuang, Bifurcations and exact solutions of the Raman soliton model in nanoscale optical waveguides with metamaterials, J. Nonl. Mod. Anal., 2021, 3, 145–165. -
-
-
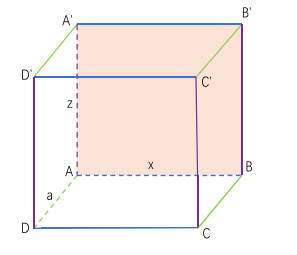
Figure 1.
The level set of
$ {H}(x, y)=h $ $ \alpha=\beta=\gamma = 0 $ $ 0<\lambda< 1 $ $ \alpha = 0 $ $ 0 <\beta=\gamma=\lambda< 1 $ $ \alpha=\beta = 0 $ $ 0 <\gamma \leq \frac{4}{7} $ $ \lambda $ -
Figure 2.
Cube
$ \mathcal{C}_1 $




 DownLoad:
DownLoad: