| Citation: |
Nina Huo, Yongkun Li. PSEUDO ALMOST PERIODIC SOLUTION OF FRACTIONAL-ORDER CLIFFORD-VALUED HIGH-ORDER HOPFIELD NEURAL NETWORKS[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 2488-2504. doi: 10.11948/20220447
|
PSEUDO ALMOST PERIODIC SOLUTION OF FRACTIONAL-ORDER CLIFFORD-VALUED HIGH-ORDER HOPFIELD NEURAL NETWORKS
-
Abstract
In this work, based on the principle of contraction mapping, we deduce sufficient conditions ensuring the existence of pseudo almost periodic solutions of fractional-order Clifford-valued high-order Hopfield neural networks (FCHHNNs). In addition, we employ a kind of Gronwall inequality to study the finite-time stability of pseudo almost periodic solutions of FCHHNNs. The results and methods of our paper are new. Finally, we give a numerical example to illustrate the effectiveness of the results obtained.
-
-
References
[1] M. S. Ali, G. Narayanan, V. Shekher, A. Alsaedi and B. Ahmad, Global Mittag-Leffler stability analysis of impulsive fractional-order complex-valued BAM neural networks with time varying delays, Commun. Nonlinear Sci. Numer. Simulat., 2020, 83, paper no. 105088. doi: 10.1016/j.cnsns.2019.105088 [2] C. Aouiti and F. Dridi, Weighted pseudo almost automorphic solutions for neutral type fuzzy cellular neural networks with mixed delays and D operator in Clifford algebra, Int. J. Syst. Sci., 2020, 51(10), 1759–1781. doi: 10.1080/00207721.2020.1777345 [3] C. Aouiti and F. Touati, Global dissipativity of Clifford-valued multidirectional associative memory neural networks with mixed delays, Comput. Appl. Math., 2020, 39, paper no. 310. doi: 10.1007/s40314-020-01367-5 [4] N. Boonsatit, G. Rajchakit, R. Sriraman, C. P. Lim and P. Agarwal, Finite-/fixed-time synchronization of delayed Clifford-valued recurrent neural networks, Adv. Differ. Equ., 2021, 2021(2021), paper no. 276. [5] S. Breuils, K. Tachibana and E. Hitzer, New Applications of Clifford's Geometric Algebra, Adv. Appl. Clifford Algebras, 2022, 32, paper no. 17. doi: 10.1007/s00006-021-01196-7 [6] S. Buchholz, A Theory of Neural Computation with Clifford Algebras, PhD thesis, University of Kiel, 2005. [7] S. Buchholz and G. Sommer, On Clifford neurons and Clifford multi-layer perceptrons, Neural Netw., 2008, 21(7), 925–935. doi: 10.1016/j.neunet.2008.03.004 [8] J. Chen, Z. Zeng and P. Jiang, Global Mittag-Leffler stability and synchronization of memristor-based fractional-order neural networks, Neural Netw., 2014, 51, 1–8. doi: 10.1016/j.neunet.2013.11.016 [9] Y. Chen, X. Zhang and Y. Xue, Global exponential synchronization of high-order quaternion Hopfield neural networks with unbounded distributed delays and time-varying discrete delays, Math. Comput. Simul., 2022, 193, 173–189. doi: 10.1016/j.matcom.2021.10.012 [10] T. Diagana, Almost Automorphic Type and Almost Periodic Type Functions in Abstract Spaces, Springer, New York, 2013. [11] L. Duan, L. Huang, Z. Guo and X. Fang, Periodic attractor for reaction-diffusion high-order Hopfield neural networks with time-varying delays, Comput. Math. Appl., 2017, 73(2), 233–245. doi: 10.1016/j.camwa.2016.11.010 [12] Z. He, C. Li, H. Li and Q. Zhang, Global exponential stability of high-order Hopfield neural networks with state-dependent impulses, Physica A, 2020, 542, paper no. 123434. doi: 10.1016/j.physa.2019.123434 [13] E. Hitzer, T. Nitta and Y. Kuroe, Applications of Clifford's geometric algebra, Adv. Appl. Clifford Algebras, 2013, 23(2), 377–404. doi: 10.1007/s00006-013-0378-4 [14] S. Huang, Y. Y. Qiao and G. C. Wen, Real and Complex Clifford Analysis, Springer, New York, 2006. [15] N. Huo and Y. Li, Finite-time Sp-almost periodic synchronization of fractional-order octonion-valued Hopfield neural networks, Chaos Solitons Fractals, 2023, 173, paper no. 113721. doi: 10.1016/j.chaos.2023.113721 [16] B. Li, Y. Cao and Y. Li, Almost periodic oscillation in distribution for octonion-valued neutral-type stochastic recurrent neural networks with D operator, Nonlinear Dyn., 2023, 111, 11371–11388. doi: 10.1007/s11071-023-08411-z [17] B. Li and Y. Li, Existence and global exponential stability of pseudo almost periodic solution for Clifford-valued neutral high-order Hopfield neural networks with leakage delays, IEEE Access, 2019, 7, 150213–150225. doi: 10.1109/ACCESS.2019.2947647 [18] Y. Li, M. Huang and B. Li, Besicovitch almost periodic solutions for fractional-order quaternion-valued neural networks with discrete and distributed delays, Math. Meth. Appl. Sci., 2022, 45(8), 4791–4808. doi: 10.1002/mma.8070 [19] Y. Li and B. Li, Pseudo compact almost automorphy of neutral type Clifford-valued neural networks with mixed delays, Discrete Contin. Dyn. Syst.-B, 2022, 27(9), 4703–4724. doi: 10.3934/dcdsb.2021248 [20] Y. Li, C. Ruan and B. Li, Existence and finite-time stability of Besicovitch almost periodic solutions of fractional-order quaternion-valued neural networks with time-varying delays, Neural Process. Lett., 2022, 54, 2127–2141. doi: 10.1007/s11063-021-10722-4 [21] Y. Li and X. Wang, Almost periodic solutions in distribution of Clifford-valued stochastic recurrent neural networks with time-varying delays, Chaos Solitons Fractals, 2021, 153, 111536. doi: 10.1016/j.chaos.2021.111536 [22] Y. Li, X. Wang and N. Huo, Weyl almost automorphic solutions in distribution sense of Clifford-valued stochastic neural networks with time-varying delays, Proc. Royal Soc. A, 2022, 478(2257), paper no. 20210719. doi: 10.1098/rspa.2021.0719 [23] Y. Li, Y. Wang and B. Li, Existence and finite-time stability of a unique almost periodic positive solution for fractional-order Lasota-Wazewska red blood cell models, Int. J. Biomath., 2020, 13(2), paper no. 2050013. doi: 10.1142/S1793524520500138 [24] Y. Liu, P. Xu, J. Lu and J. Liang, Global stability of Clifford-valued recurrent neural networks with time delays, Nonlinear Dyn., 2016, 84(2), 767–777. doi: 10.1007/s11071-015-2526-y [25] D. Luo, Q. Jiang and Q. Wang, Anti-periodic solutions on Clifford-valued high-order Hopfield neural networks with multi-proportional delays, Neurocomputing, 2022, 472, 1–11. doi: 10.1016/j.neucom.2021.11.001 [26] W. Lv and B. Li, Existence and global attractivity of pseudo almost periodic solutions for Clifford-valued fuzzy neural networks with proportional delays, Math., 2021, 9(24), paper no. 3306. doi: 10.3390/math9243306 [27] I. Podlubny, Fractional Differential Equations, Mathematics in Science and Engineering, Academic Press, New York, 1999. [28] G. Rajchakit, P. Chanthorn, P. Kaewmesri, R. Sriraman and C. P. Lim, Global Mittag-Leffler stability and stabilization analysis of fractional-order quaternion-valued memristive neural networks, Math., 2020, 8(3), paper no. 422. doi: 10.3390/math8030422 [29] G. Rajchakit, P. Chanthorn, M. Niezabitowski, R. Raja, D. Baleanu and A. Pratap, Impulsive effects on stability and passivity analysis of memristor-based fractional-order competitive neural networks, Neurocomputing, 2020, 417, 290–301. doi: 10.1016/j.neucom.2020.07.036 [30] G. Rajchakit, A. Pratap, R. Raja, J. Cao, J. Alzabut and C. Huang, Hybrid control scheme for projective lag synchronization of Riemann-Liouville sense fractional order memristive BAM neural networks with mixed delays, Math., 2019, 7(8), paper no. 759. doi: 10.3390/math7080759 [31] G. Rajchakit, R. Sriraman, N. Boonsatit, P. Hammachukiattikul, C. P. Lim and P. Agarwal, Global exponential stability of Clifford-valued neural networks with time-varying delays and impulsive effects, Adv. Differ. Equ., 2021, 2021(2021), paper no. 208. [32] G. Rajchakit, R. Sriraman, C. P. Lim and B. Unyong, Existence, uniqueness and global stability of Clifford-valued neutral-type neural networks with time delays, Math. Comput. Simul., 2022, 201, 508–527. doi: 10.1016/j.matcom.2021.02.023 [33] G. Rajchakit, R. Sriraman, P. Vignesh and C. P. Lim, Impulsive effects on Clifford-valued neural networks with time-varying delays: An asymptotic stability analysis, Appl. Math. Comput., 2021, 407, paper no. 126309. [34] C. Xu, M. Liao, P. Li, L. Yao, Q. Qin and Y. Shang, Chaos control for a fractional-order jerk system via time delay feedback controller and mixed controller, Frac. Fract., 2021, 5(4), paper no. 257. doi: 10.3390/fractalfract5040257 [35] C. Xu, M. Liao, P. Li and S. Yuan, Impact of leakage delay on bifurcation in fractional-order complex-valued neural networks, Chaos Solitons Fractals, 2021, 142, paper no. 110535. doi: 10.1016/j.chaos.2020.110535 [36] C. Xu, Z. Liu, M. Liao, P. Li, Q. Xiao and S. Yuan, Fractional-order bidirectional associate memory (BAM) neural networks with multiple delays: The case of Hopf bifurcation, Math. Comput. Simul., 2021, 182, 471–494. doi: 10.1016/j.matcom.2020.11.023 [37] Y. Xu, T. Lin, X. Liu and W. Li, Exponential bipartite synchronization of fractional-order multilayer signed networks via hybrid impulsive control, IEEE Trans. Cyber., 2023, 53, 3926–3938. doi: 10.1109/TCYB.2022.3190413 [38] Y. Xu, F. Sun and W. Li, Exponential synchronization of fractional-order multilayer coupled neural networks with reaction-diffusion terms via intermittent control, Neural Comput. Appl., 2021, 33(23), 16019–16032. doi: 10.1007/s00521-021-06214-0 [39] Y. Xu, J. Yu, W. Li and J. Feng, Global asymptotic stability of fractional-order competitive neural networks with multiple time-varying-delay links, Appl. Math. Comput., 2021, 389, paper no. 125498. [40] H. Ye, J. Gao and Y. Ding, A generalized Gronwall inequality and its application to a fractional differential equation, J. Math. Anal. Appl., 2007, 328, 1075–1081. doi: 10.1016/j.jmaa.2006.05.061 [41] J. Yu, C. Hu and H. Jiang, $\alpha$-stability and $\alpha$-synchronization for fractional-order neural networks, Neural Netw., 2012, 35, 82–87. doi: 10.1016/j.neunet.2012.07.009 CrossRef $\alpha$-stability and
$\alpha$ [42] F. Zhang, T. Huang, Q. Wu and Z. Zeng, Multistability of delayed fractional-order competitive neural networks, Neural Netw., 2021, 140, 325–335. doi: 10.1016/j.neunet.2021.03.036 [43] S. Zhang, Y. Yu and J. Yu, LMI conditions for global stability of fractional-order neural networks, IEEE Trans. Neural Netw. Learn. Syst., 2016, 28(10), 2423–2433. -
-
Figures(9)
Export File
Citation
Nina Huo, Yongkun Li. PSEUDO ALMOST PERIODIC SOLUTION OF FRACTIONAL-ORDER CLIFFORD-VALUED HIGH-ORDER HOPFIELD NEURAL NETWORKS[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 2488-2504. doi: 10.11948/20220447
Format
Content
DownLoad:
-
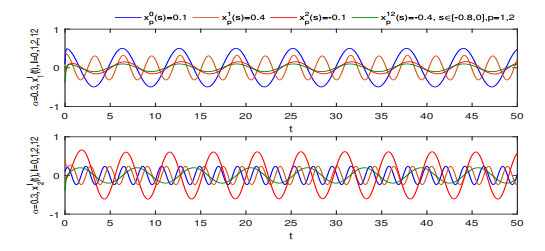
Figure 1.
Curves of
$ x_{1}^{l}(t) $ $ x_{2}^{l}(t) $ $ \alpha=0.3, l=0, 1, 2, 12 $ -
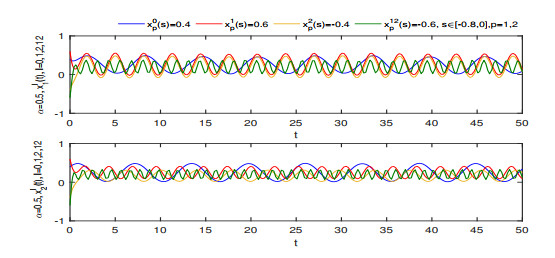
Figure 2.
Curves of
$ x_{1}^{l}(t) $ $ x_{2}^{l}(t) $ $ \alpha=0.5, l=0, 1, 2, 12 $ -
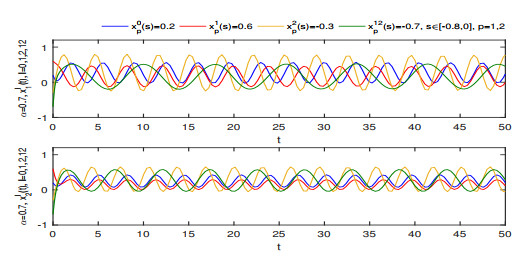
Figure 3.
Curves of
$ x_{1}^{l}(t) $ $ x_{2}^{l}(t) $ $ \alpha=0.7, l=0, 1, 2, 12 $ -
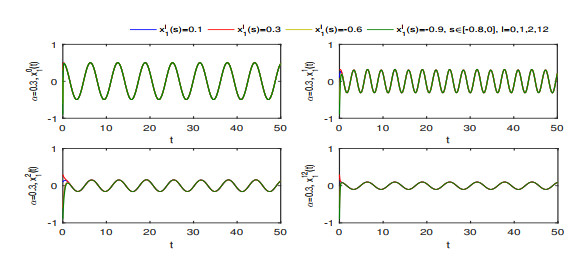
Figure 4.
Finite-time stability of
$ x_{1}^{0}(t) $ $ x_{1}^{1}(t) $ $ x_{1}^{2}(t) $ $ x_{1}^{12}(t) $ $ \alpha=0.3 $ -
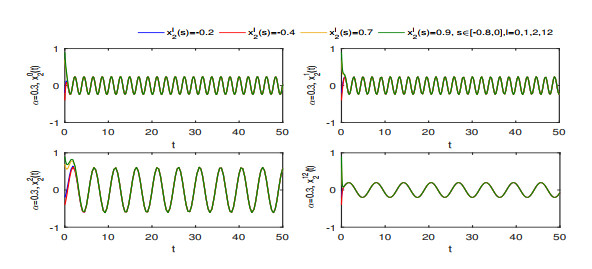
Figure 5.
Finite-time stability of
$ x_{2}^{0}(t) $ $ x_{2}^{1}(t) $ $ x_{2}^{2}(t) $ $ x_{2}^{12}(t) $ $ \alpha=0.3$ -
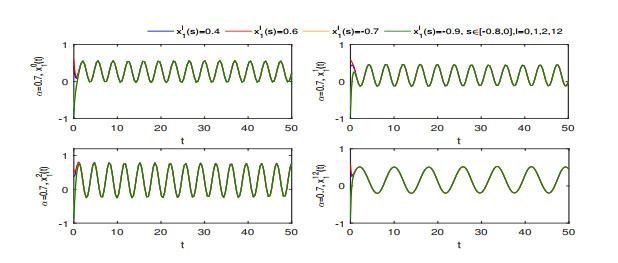
Figure 6.
Finite-time stability of
$ x_{1}^{0}(t) $ $ x_{1}^{1}(t) $ $ x_{1}^{2}(t) $ $ x_{1}^{12}(t) $ $ \alpha=0.5$ -
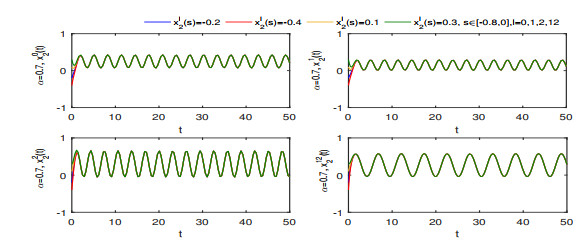
Figure 7.
Finite-time stability of
$ x_{2}^{0}(t) $ $ x_{2}^{1}(t) $ $ x_{2}^{2}(t) $ $ x_{2}^{12}(t) $ $ \alpha=0.5 $ -
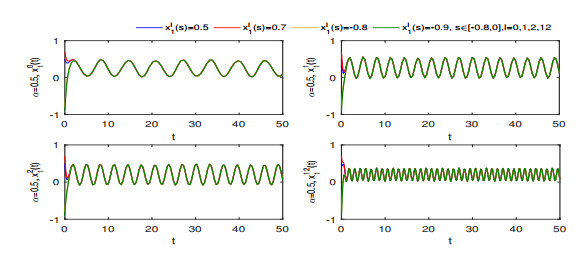
Figure 8.
Finite-time stability of
$ x_{1}^{0}(t) $ $ x_{1}^{1}(t) $ $ x_{1}^{2}(t) $ $ x_{1}^{12}(t) $ $ \alpha=0.7 $ -
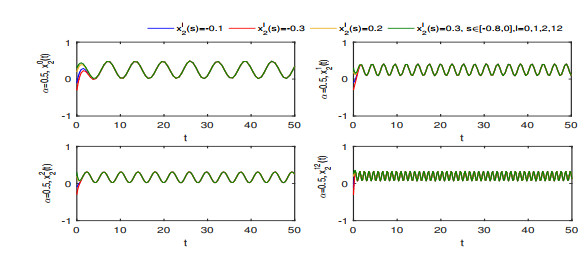
Figure 9.
Finite-time stability of
$ x_{2}^{0}(t) $ $ x_{2}^{1}(t) $ $ x_{2}^{2}(t) $ $ x_{2}^{12}(t) $ $ \alpha=0.7 $