| Citation: |
Mo Faheem, Arshad Khan, Akmal Raza. AN EFFICIENT WAVELET COLLOCATION METHOD BASED ON HERMITE POLYNOMIALS FOR A CLASS OF 2D QUASI-LINEAR ELLIPTIC EQUATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(3): 1198-1221. doi: 10.11948/20220530
|
AN EFFICIENT WAVELET COLLOCATION METHOD BASED ON HERMITE POLYNOMIALS FOR A CLASS OF 2D QUASI-LINEAR ELLIPTIC EQUATIONS
-
Abstract
A wavelet collocation method based on Hermite polynomials is proposed for the study of a class of 2D quasi-linear elliptic partial differential equations (PDEs) that arise frequently in applied mathematics, electromagnetic theory, nonlinear optics, weather forecasting, etc. The application of Hermite wavelets and their integration to 2D quasi-linear elliptic PDEs yielded a system of equations. For the theoretical aspect, the upper bound of the error norm is established to guarantee the convergence of the method. The proposed approach has an exponential rate of convergence, so it converges very rapidly. The proposed method can be uniformly adapted to investigate the solution of 2D singularly perturbed elliptic PDEs without modifying the current scheme. Some numerical simulations have been done to validate the theoretical findings. The maximum absolute errors are calculated for different numbers of collocation grids. The comparison of numerical findings with the existing methods concludes the superiority of the proposed method.
-
-
References
[1] M. P. Alam and A. Khan, A new numerical algorithm for time-dependent singularly perturbed differential-difference convection–diffusion equation arising in computational neuroscience, Comput. Appl. Math., 2022, 41(8), 402. doi: 10.1007/s40314-022-02102-y [2] M. P. Alam, D. Kumar and A. Khan, Trigonometric quintic B-spline collocation method for singularly perturbed turning point boundary value problems, Intern. J. Comput. Math., 2021, 98(5), 1029-1048. doi: 10.1080/00207160.2020.1802016 [3] B. Bialecki, G. Fairweather and A. Karageorghis, Matrix decomposition algorithms for modified spline collocation for Helmholtz problems, SIAM J. Sci. Comput., 2003, 24(5), 1733-1753. doi: 10.1137/S106482750139964X [4] B. Bialecki and Z. Wang, Modified nodal cubic spline collocation for elliptic equations, Numer. Methods Partial Differ. Equ., 2012, 28(6), 1817-1839. doi: 10.1002/num.20704 [5] C. C. Christara, Quadratic spline collocation methods for elliptic partial differential equations, BIT Numer. Math., 1994, 34(1), 33-61. doi: 10.1007/BF01935015 [6] R. Courant and D. Hilbert, Methods of Mathematical Physics: Interscience, New York, 1962, 19532. [7] L. Demkowicz and N. Heuer, Robust DPG method for convection-dominated diffusion problems, SIAM J. Numer. Anal., 2013, 51(5), 2514-2537. doi: 10.1137/120862065 [8] M. Faheem and A. Khan, A collocation method for time-fractional diffusion equation on a metric star graph with $ \eta$ edges, Math. Meth. Appl. Sci., 2023. [9] M. Faheem and A. Khan, A wavelet collocation method based on Gegenbauer scaling function for solving fourth-order time-fractional integro-differential equations with a weakly singular kernel, Appl. Numer. Math., 2023, 184, 197-218. doi: 10.1016/j.apnum.2022.10.003 [10] M. Faheem, A. Khan and E. El-Zahar, On some wavelet solutions of singular differential equations arising in the modeling of chemical and biochemical phenomena, Adv. Differ. Equa., 2020, 2020, 526. doi: 10.1186/s13662-020-02965-7 [11] M. Faheem, A. Khan and Ö. Oruç, A generalized Gegenbauer wavelet collocation method for solving p-type fractional neutral delay differential and delay partial differential equations, Math. Sci., 2022. [12] M. Faheem, A. Khan and P. J. Wong, A Legendre wavelet collocation method for 1D and 2D coupled time-fractional nonlinear diffusion system, Comput. Math. Appl., 2022, 128, 214-238. doi: 10.1016/j.camwa.2022.10.014 [13] M. Faheem, A. Raza and A. Khan, Collocation methods based on Gegenbauer and Bernoulli wavelets for solving neutral delay differential equations, Math. Comput. Simul., 2021, 180, 72-92. doi: 10.1016/j.matcom.2020.08.018 [14] R. Glowinski, Wavelet solution of linear and nonlinear elliptic, Parab. Hyper. Problems One Space Dimen., 1989, 1-79. [15] A. Hadjidimos, E. N. Houstis, J. R. Rice and E. Vavalis, Iterative line cubic spline collocation methods for elliptic partial differential equations in several dimensions, SIAM J. Sci. Comput., 1993, 14(3), 715-734. doi: 10.1137/0914045 [16] M. H. Heydari, M. R. Hooshmandasl and F. Mohammadi, Legendre wavelets method for solving fractional partial differential equations with Dirichlet boundary conditions, Appl. Math. Comput., 2014, 234, 267-276. [17] E. N. Houstis, E. Vavalis and J. R. Rice, Convergence of O(h. 4) cubic spline collocation methods for elliptic partial differential equations, SIAM J. Numer. Anal., 1988, 25(1), 54-74. doi: 10.1137/0725006 [18] M. Jain, R. Jain and R. Mohanty, Fourth-order difference methods for the system of 2D nonlinear elliptic partial differential equations, Numer. Methods Partial Differ. Equ., 1991, 7(3), 227-244. doi: 10.1002/num.1690070303 [19] M. K. Jain, R. Jain and R. Mohanty, A fourth-order difference method for elliptic equations with nonlinear first derivative terms, Numer. Methods Partial Differ. Equ., 1989, 5(2), 87-95. doi: 10.1002/num.1690050203 [20] N. Jha and N. Kumar, A fourth-order accurate quasi-variable mesh compact finite-difference scheme for two-space dimensional convection-diffusion problems, Adv. Differ. Equ., 2017, 2017(1), 1-13. doi: 10.1186/s13662-016-1057-2 [21] A. Khan, M. Faheem and A. Raza, Solution of third-order Emden-Fowler-type equations using wavelet methods, Eng. Comput., 2021. [22] J. Li, Quasioptimal uniformly convergent finite element methods for the elliptic boundary layer problem, Comput. Math. Appl., 1997, 33(10), 11-22. doi: 10.1016/S0898-1221(97)00073-4 [23] J. Li, Global pointwise error estimates for uniformly convergent finite element methods for the elliptic boundary layer problem, Comput. Math. Appl., 1998, 36(1), 59-67. doi: 10.1016/S0898-1221(98)00109-6 [24] J. Li and I. M. Navon, Uniformly convergent finite element methods for singularly perturbed elliptic boundary value problems Ⅰ: Reaction-diffusion type, Comput. Math. Appl., 1998, 35(3), 57-70. doi: 10.1016/S0898-1221(97)00279-4 [25] N. Li, H. Su, D. Gui and X. Feng, Multiquadric RBF-FD method for the convection-dominated diffusion problems base on Shishkin nodes, Int. J. Heat Mass Transf., 2018, 118, 734-745. doi: 10.1016/j.ijheatmasstransfer.2017.11.011 [26] R. Mohanty, Order h4 difference methods for a class of singular two space elliptic boundary value problems, J. Comput. Appl. Math., 1997, 81(2), 229-247. doi: 10.1016/S0377-0427(97)00058-7 [27] R. Mohanty, A new high accuracy finite difference discretization for the solution of 2D nonlinear biharmonic equations using coupled approach, Numer. Methods Partial Differ. Equ., 2010, 26(4), 931-944. doi: 10.1002/num.20465 [28] R. Mohanty, M. Jain and D. Dhall, High accuracy cubic spline approximation for two dimensional quasi-linear elliptic boundary value problems, Appl. Math. Model., 2013, 37(1-2), 155-171. doi: 10.1016/j.apm.2012.02.020 [29] R. Mohanty, G. Manchanda and A. Khan, Compact half step approximation in exponential form for the system of 2D second-order quasi-linear elliptic partial differential equations, J. Differ. Equ. Appl., 2019, 25(5), 716-749. doi: 10.1080/10236198.2019.1624737 [30] R. K. Mohanty and N. Setia, A new compact high order off-step discretization for the system of 2D quasi-linear elliptic partial differential equations, Adv. Differ. Equa., 2013, 2013, 223. doi: 10.1186/1687-1847-2013-223 [31] Ö. Oruç, A computational method based on Hermite wavelets for two-dimensional Sobolev and regularized long wave equations in fluids, Numer. Methods Partial Differ. Equ., 2018, 34, 1693-1715. doi: 10.1002/num.22232 [32] Ö. Oruç, A numerical procedure based on Hermite wavelets for two-dimensional hyperbolic telegraph equation, Eng. Comput., 2018, 34, 741-755. doi: 10.1007/s00366-017-0570-6 [33] Ö. Oruç, A non-uniform Haar wavelet method for numerically solving two-dimensional convection-dominated equations and two-dimensional near singular elliptic equations, Comput. Math. Appl., 2019, 77(7), 1799-1820. doi: 10.1016/j.camwa.2018.11.018 [34] S. Qian and J. Weiss, Wavelets and the numerical solution of boundary value problems, Appl. Math. Lett., 1993, 6(1), 47-52. doi: 10.1016/0893-9659(93)90147-F [35] S. Qian and J. Weiss, Wavelets and the numerical solution of partial differential equations, J. Comput. Phy., 1993, 106(1), 155-175. doi: 10.1006/jcph.1993.1100 [36] P. Rahimkhani, Y. Ordokhani and E. Babolian, Fractional-order Bernoulli wavelets and their applications, Appl. Math. Model., 2016, 40(17-18), 8087-8107. doi: 10.1016/j.apm.2016.04.026 [37] P. Rahimkhani, Y. Ordokhani and E. Babolian, A new operational matrix based on Bernoulli wavelets for solving fractional delay differential equations, Nume. Algor., 2017, 74(1), 223-245. doi: 10.1007/s11075-016-0146-3 [38] A. Raza, A. Khan, P. Sharma and K. Ahmad, Solution of singularly perturbed differential difference equations and convection delayed dominated diffusion equations using Haar wavelet, Math. Sci., 2021, 15(2), 123-136. doi: 10.1007/s40096-020-00355-4 [39] U. Saeed and M. Rehman, Hermite wavelet method for fractional delay differential equations, J. Differ. Equa., 2014, 2014, 359093. [40] H. Saeedi, M. M. Moghadam, N. Mollahasani and G. Chuev, A CAS wavelet method for solving nonlinear Fredholm integro-differential equations of fractional order, Commun. Nonlinear Sci. Numer. Simul., 2011, 16(3), 1154-1163. [41] G. Saldanha, A fourth-order finite difference scheme for a system of a 2D nonlinear elliptic partial differential equations, Numer. Methods Partial Differ. Equ., 2001, 17(1), 43-53. doi: 10.1002/1098-2426(200101)17:1<43::AID-NUM3>3.0.CO;2-H [42] G. Saldanha and U. Ananthakrishnaiah, A fourth-order finite difference scheme for two-dimensional nonlinear elliptic partial differential equations, Numer. Methods Partial Differ. Equ., 1995, 11(1), 33-40. doi: 10.1002/num.1690110104 [43] S. Shiralashetti and S. Kumbinarasaiah, Hermite wavelets operational matrix of integration for the numerical solution of nonlinear singular initial value problems, Alexan. Eng. Jour., 2018, 57(4), 2591-2600. [44] S. Singh and S. Singh, High order convergent modified nodal bi-cubic spline collocation method for elliptic partial differential equation, Numer. Methods Partial Differ. Equ., 2020, 36(5), 1028-1043. [45] Z. Yang and S. Liao, A HAM-based wavelet approach for nonlinear partial differential equations: two dimensional Bratu problem as an application, Commun. Nonlinear Sci. Numer. Simul., 2017, 53, 249-262. [46] S. A. Yousefi, Legendre wavelets method for solving differential equations of Lane-Emden type, Appl. Math. Comput., 2006, 181(2), 1417-1422. [47] F. Zhou and X. Xu, The third kind Chebyshev wavelets collocation method for solving the time-fractional convection diffusion equations with variable coefficients, Appl. Math. Comput., 2016, 280, 11-29. -
-
Figures(14) / Tables(12)
Export File
Citation
Mo Faheem, Arshad Khan, Akmal Raza. AN EFFICIENT WAVELET COLLOCATION METHOD BASED ON HERMITE POLYNOMIALS FOR A CLASS OF 2D QUASI-LINEAR ELLIPTIC EQUATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(3): 1198-1221. doi: 10.11948/20220530
Format
Content
DownLoad:
-
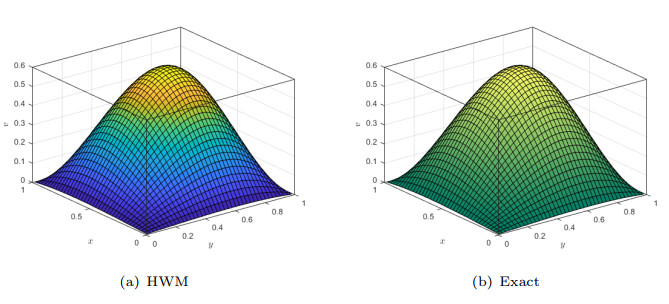
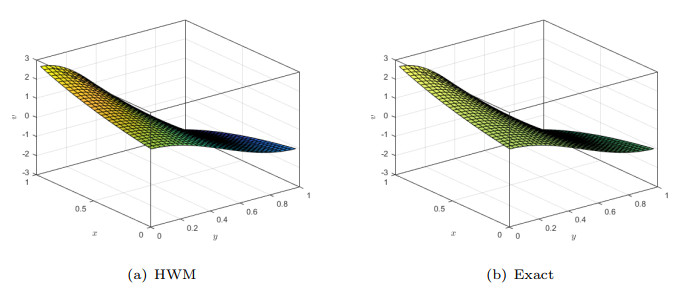
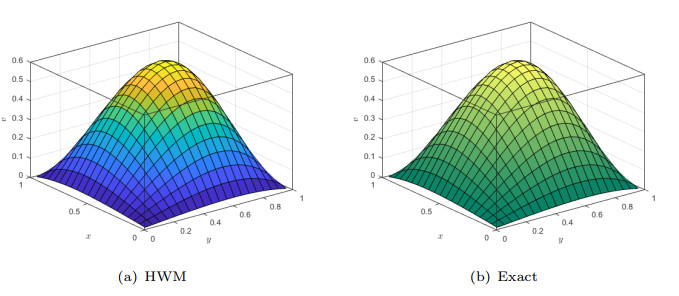
Figure 1.
A comparison of HWM and exact solution of Example 6.1 for
$ \mathit{k}_{1}=\mathit{k}_{2}=3,\;\mathit{M}_{1}=\mathit{M}_{2}=5 $ -
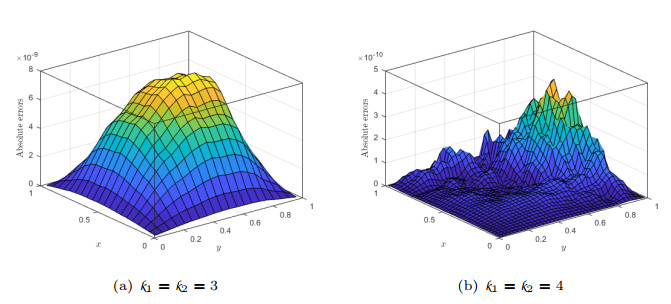
Figure 2.
Behavior of AEs of HWM for Example 6.1 for different
$ \mathit{k}_{1},\;\mathit{k}_{2} $ $ \mathit{M}_{1}=\mathit{M}_{2}=5 $ -
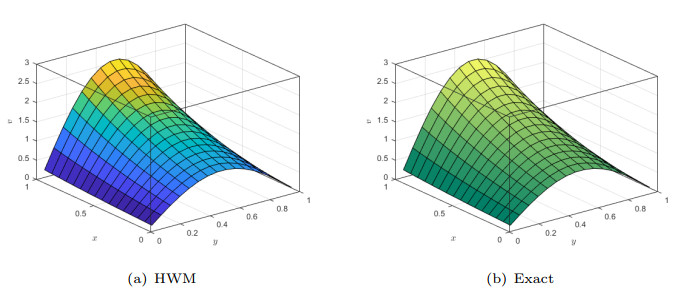
Figure 3.
A comparison of HWM and exact solution of Example 6.2 for
$ \mathit{k}_{1}=\mathit{k}_{2}=4,\;\mathit{M}_{1}=\mathit{M}_{2}=5 $ -
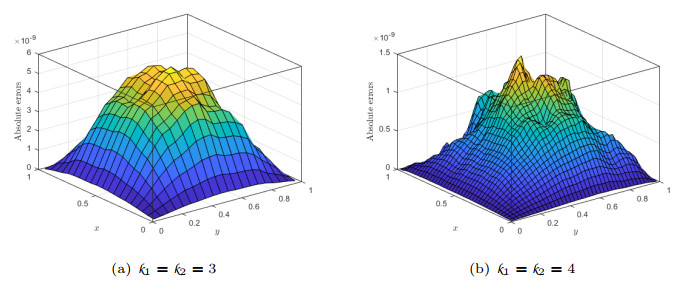
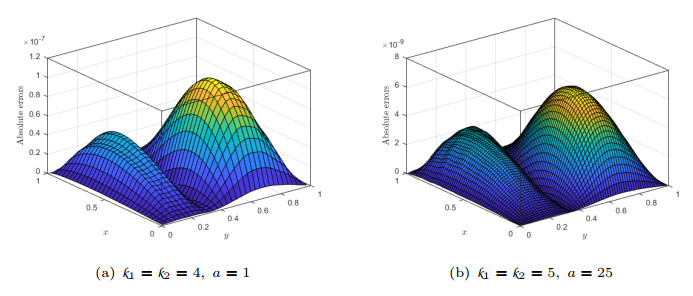
Figure 4.
Behavior of AEs of HWM for Example 6.2 for different
$ \mathit{k}_{1},\;\mathit{k}_{2} $ $ \mathit{M}_{1}=\mathit{M}_{2}=5 $ -
Figure 5.
A comparison of HWM and exact solution of Example 6.3 for
$ \mathit{k}_{1}=\mathit{k}_{2}=3,\;\mathit{M}_{1}=\mathit{M}_{2}=4 $ -
Figure 6.
Behavior of AEs of HWM for Example 6.3 for different
$ \mathit{k}_{1},\;\mathit{k}_{2} $ $ \mathit{M}_{1}=\mathit{M}_{2}=4 $ -
Figure 7.
A comparison of HWM and exact solution of Example 6.4 for
$ \mathit{k}_{1}=\mathit{k}_{2}=4,\;\mathit{M}_{1}=\mathit{M}_{2}=4 $ -
Figure 8.
Behavior of AEs of HWM for Example 6.4 for different
$ \mathit{k}_{1},\;\mathit{k}_{2} $ $ \mathit{M}_{1}=\mathit{M}_{2}=4 $ -
Figure 9.
A comparison of HWM and exact solution of Example 6.5 for
$ \mathit{k}_{1}=\mathit{k}_{2}=4,\;\mathit{M}_{1}=\mathit{M}_{2}=4 $ -
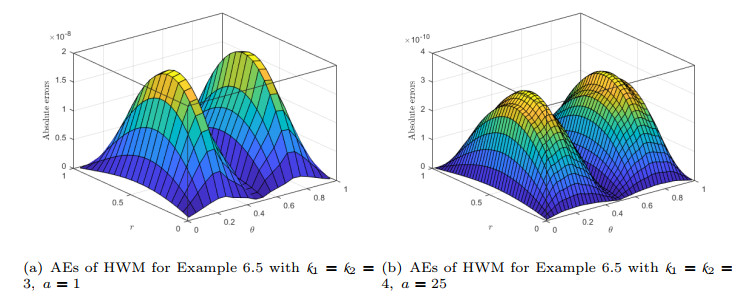
Figure 10.
AEs of HWM for Example 6.5 for different
$ \mathit{k}_{1},\;\mathit{k}_{2} $ $ \mathit{M}_{1}=\mathit{M}_{2}=4 $ -
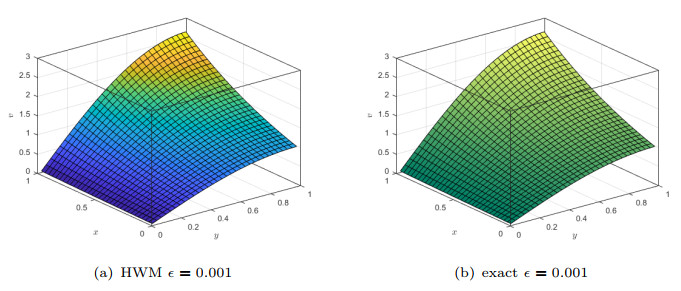
Figure 11.
HWM and exact solutions for
$ \mathit{M}_{1}=\mathit{M}_{2}=2,\; \mathit{k}_{1}=\mathit{k}_{2}=5 $ $ \epsilon $ -
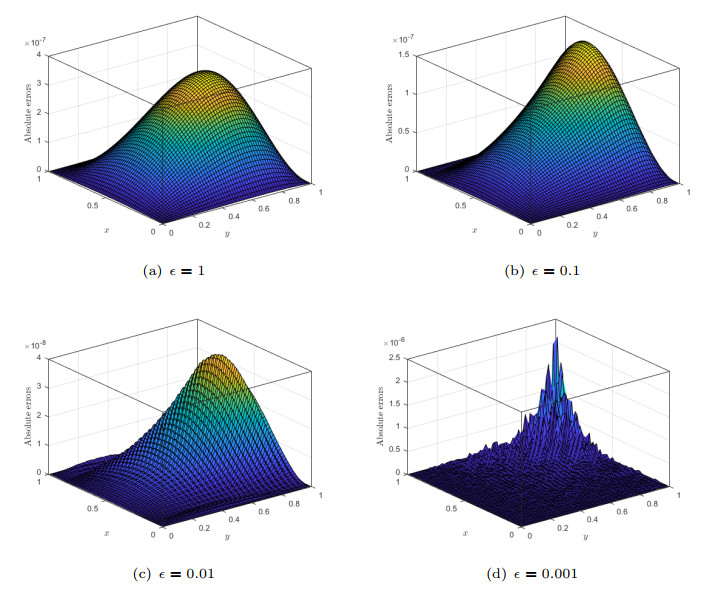
Figure 12.
Effect of
$ \epsilon $ $ \mathit{k}_{1}=\mathit{k}_{2}=5,\;\mathit{M}_{1}=\mathit{M}_{2}=2 $ -
Figure 13.
Effect of
$ \epsilon $ $ \mathit{k}_{1}=\mathit{k}_{2}=6,\;\mathit{M}_{1}=\mathit{M}_{2}=2 $ -
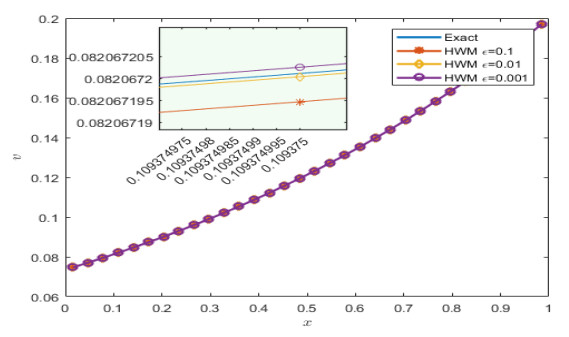
Figure 14.
Comparison of Exact and HWM solutions of Example 6.6 at
$ \mathit{y}=0.5 $ $ \epsilon $