| Citation: |
Zhiyuan Liu, Shurong Sun. SOLVABILITY AND STABILITY OF MULTI-TERM FRACTIONAL DELAY Q-DIFFERENCE EQUATION[J]. Journal of Applied Analysis & Computation, 2024, 14(3): 1177-1197. doi: 10.11948/20220411
|
SOLVABILITY AND STABILITY OF MULTI-TERM FRACTIONAL DELAY Q-DIFFERENCE EQUATION
-
Abstract
The research of multi-term fractional differential equations has attracted the attention of scholars and obtained abundant results in recent years. However, there are few studies on the multi-term fractional q-difference equations. In this paper, we investigate boundary value problems for multi-term fractional delay q-difference equation. By virtue of Banach contraction mapping principle and Leray-Schauder nonlinear alternative theorem, we obtain the uniqueness and existence of the solution. In addition, we get four different results for functional stability, including Ulam-Hyres stability, generalized Ulam-Hyres stability, Ulam-Hyres Rassias stability and generalized Ulam-Hyres Rassias stability. Finally, give relevant examples to demonstrate the main results.
-
-
References
[1] F. Abdullah, Simulations of hirschsprung's disease using fractional differential equations, Sains Malaysiana, 2013, 42(5), 661-666. [2] R. Agarwal, Certain fractional q-integrals and q-derivatives, Mathematical Proceedings of the Cambridge Philosophical Society, 1969, 66(2), 365-370. doi: 10.1017/S0305004100045060 [3] W. Al-Salam, Some fractional q-integrals and q-derivatives, Proceedings of the Edinburgh Mathematical Society, 1966, 15(2), 135-140. doi: 10.1017/S0013091500011469 [4] M. Annaby and Z. Mansour, q-Fractional Calculus and Equations, Springer Berlin, Heidelberg, 2012. [5] C. Arreche and Y. Zhang, Computing differential Galois groups of second-order linear q-difference equations, Advances in Applied Mathematics, 2022, 132, 102273. doi: 10.1016/j.aam.2021.102273 [6] A. Boutiara, Multi-term fractional q-difference equations with q-integral boundary conditions via topological degree theory, Communications in Optimization Theory, 2021, 1, 1-16. [7] A. Carpinteri and F. Mainardi, Fractals and Fractional Calculus in Continuum Mechanics, Springer, Verlag, 2014. [8] A. Dabiri, E. Butcher and M. Nazari, Coefficient of restitution in fractional viscoelastic compliant impacts using fractional Chebyshev collocation, Journal of Sound and Vibration, 2017, 388, 230-244. doi: 10.1016/j.jsv.2016.10.013 [9] M. El-Shahed and J. Nieto, Nontrivial solutions for a nonlinear multi-point boundary value problem of fractional order, Computers and Mathematics with Applications, 2010, 59(11), 3438-3443. doi: 10.1016/j.camwa.2010.03.031 [10] T. Ernst, q-Bernoulli and q-Euler polynomials, an umbral approach, International Journal of Difference Equations, 2006, 1(1), 31-80. [11] Z. Feng, M. Ming, J. Ling, X. Xiao, Z. Yang and F. Wan, Fractional delay filter based repetitive control for precision tracking: Design and application to a piezoelectric nanopositioning stage, Mechanical Systems and Signal Processing, 2022, 164, 108249. doi: 10.1016/j.ymssp.2021.108249 [12] H. Guo, Algebra of q-difference operators, affine vertex algebras, and their modules, Journal of Algebra, 2021, 585, 69-88. doi: 10.1016/j.jalgebra.2021.06.007 [13] Y. Guo and Y. Li, Bipartite leader-following synchronization of fractional-order delayed multilayer signed networks by adaptive and impulsive controllers, Applied Mathematics and Computation, 2022, 430, 127243. doi: 10.1016/j.amc.2022.127243 [14] F. Jackson, On q-difference equations, American Journal of Mathematics, 1910, 32(4), 305-314. doi: 10.2307/2370183 [15] X. Li, Z. Han and S. Sun, Eigenvalue problems of fractional q-difference equations with generalized p-Laplacian, Applied Mathematics Letters, 2016, 57, 46-53. doi: 10.1016/j.aml.2016.01.003 [16] Y. Li and N. Song, A note on q-difference operator and related limit direction, Acta Mathematica Scientia, 2018, 38(6), 1678-1688. doi: 10.1016/S0252-9602(18)30839-7 [17] K. Ma and S. Sun, Finite-time stability of linear fractional time-delay q-difference dynamical system, Journal of Applied Mathematics and Computing, 2018, 57, 591-604. doi: 10.1007/s12190-017-1123-2 [18] J. Mao, Z. Zhao and C. Wang, The unique iterative positive solution of fractional boundary value problem with q-difference, Applied Mathematics Letters, 2020, 100, 106002. doi: 10.1016/j.aml.2019.106002 [19] S. Nemati and Z. Kalansara, A low-cost computational method for solving nonlinear fractional delay differential equations, Communications in Nonlinear Science and Numerical Simulation, 2022, 114, 106650. doi: 10.1016/j.cnsns.2022.106650 [20] C. Peng and H. Huang, The growth of meromorphic solutions for q-difference Painleve Ⅳ equation, Journal of Mathematical Analysis and Applications, 2020, 492(2), 124485. doi: 10.1016/j.jmaa.2020.124485 [21] G. Rahman, R. Agarwal and D. Ahmad, Existence and stability analysis of nth order multi term fractional delay differential equation, Chaos, Solitons and Fractals, 2022, 155, 111709. doi: 10.1016/j.chaos.2021.111709 [22] F. A. Rihan, D. H. A. Rahman, S. Lakshmanan and A. S. Alkhajeh, A time delay model of tumour-immune system interactions: Global dynamics, parameter estimation, sensitivity analysis, Applied Mathematics and Computation, 2014, 232, 606-623. doi: 10.1016/j.amc.2014.01.111 [23] R. Rizwan and A. Zada, Existence theory and Ulam's stabilities of fractional Langevin equation, Qualitative Theory of Dynamical Systems, 2021, 20, 57. doi: 10.1007/s12346-021-00495-5 [24] J. Solomon and L. Janos, Even continuity and the Banach contraction principle, Proceedings of the American Mathematical Society, 1978, 69(1), 166-168. doi: 10.1090/S0002-9939-1978-0500891-8 [25] P. J. Torvik and R. L. Bagley, On the appearance of the fractional derivative in the behavior of real materials, Journal of Applied Mechanics, 1984, 51(2), 294-298. doi: 10.1115/1.3167615 [26] H. Waheed, A. Zada, R. Rizwan and I. Popa, Hyers-Ulam stability for a coupled system of fractional differential equation with p-Laplacian operator having integral boundary conditions, Qualitative Theory of Dynamical Systems, 2022, 21, 92. [27] X. Wu, S. Liu and H. Wang, Asymptotic stability and synchronization of fractional delayed memristive neural networks with algebraic constraints, Communications in Nonlinear Science and Numerical Simulation, 2022, 114, 106694. [28] C. Xu, D. Mu, Y. Pan, C. Aouiti, Y. Pang and L. Yao, Probing into bifurcation for fractional-order BAM neural networks concerning multiple time delays, Journal of Computational Science, 2022, 62, 101701. [29] Y. Yan and C. Kou, Stability analysis for a fractional differential model of HIV infection of CD4+ T-cells with time delay, Mathematics and Computers in Simulation, 2012, 82(9), 1572-1585. -
-
Figures(1)
Export File
Citation
Zhiyuan Liu, Shurong Sun. SOLVABILITY AND STABILITY OF MULTI-TERM FRACTIONAL DELAY Q-DIFFERENCE EQUATION[J]. Journal of Applied Analysis & Computation, 2024, 14(3): 1177-1197. doi: 10.11948/20220411
Format
Content
DownLoad:
-
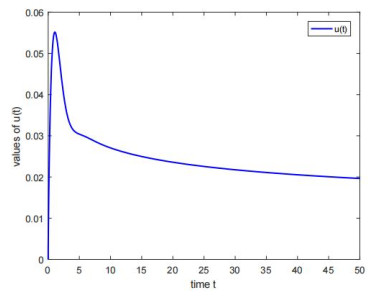
Figure 1.
Illustration of proof