| Citation: |
Yuanlu Wang, Jiantao Jiang, Jing An. SPECTRAL-GALERKIN APPROXIMATION BASED ON REDUCED ORDER SCHEME FOR FOURTH ORDER EQUATION AND ITS EIGENVALUE PROBLEM WITH SIMPLY SUPPORTED PLATE BOUNDARY CONDITIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 61-83. doi: 10.11948/20230018
|
SPECTRAL-GALERKIN APPROXIMATION BASED ON REDUCED ORDER SCHEME FOR FOURTH ORDER EQUATION AND ITS EIGENVALUE PROBLEM WITH SIMPLY SUPPORTED PLATE BOUNDARY CONDITIONS
-
Abstract
We develop in this paper a high-order numerical method for fourth-order equation with simply supported plate boundary conditions in a circular domain. By introducing an auxiliary function and using the dimension reduction technique, we reduce the fourth-order problem to a one-dimensional second-order coupled problem. Based on the one-dimensional second-order coupled problem, we prove the uniqueness of the weak solution and approximation solutions and the error estimation between them. Moreover, we extend the approach to fourth-order eigenvalue problem with simply supported plate boundary conditions in a circular domain. Finally, we carry out some numerical experiments to validate the theoretical analysis and algorithm.
-
-
References
[1] S. Abbasbandy, E. Shivanian, K. H. AL-Jizani, et al., Pseudospectral meshless radial point interpolation for generalized biharmonic equation subject to simply supported and clamped boundary conditions, Engineering Analysis with Boundary Elements, 2021, 125, 23-32. doi: 10.1016/j.enganabound.2021.01.004 [2] J. An, H. Li and Z. Zhang, Spectral-Galerkin approximation and optimal error estimate for biharmonic eigenvalue problems in circular/spherical/elliptical domains, Numerical Algorithms, 2020, 84(2), 427-455. doi: 10.1007/s11075-019-00760-4 [3] J. An and Z. Zhang, An efficient spectral-Galerkin approximation and error analysis for Maxwell transmission eigenvalue problems in spherical geometries, Journal of Scientific Computing, 2018, 75(1), 157-181. doi: 10.1007/s10915-017-0528-2 [4] W. Bao, L. Chen, X. Jiang, et al., A Jacobi spectral method for computing eigenvalue gaps and their distribution statistics of the fractional Schrödinger operator, Journal of Computational Physics, 2020, 421(15), 109733. [5] C. Canuto, Eigenvalue approximations by mixed methods, RAIRO. Analyse NuméRique, 1978, 12(1), 27-50. doi: 10.1051/m2an/1978120100271 [6] L. Chen, J. Shen and C. Xu, A triangular spectral method for the Stokes equations, Numerical Mathematics: Theory, Methods and Applications, 2011, 42, 158-179. [7] W. Chen and Q. Lin, Approximation of an eigenvalue problem associated with the stokes problem by the stream function-vorticity-pressure method, Applications of Mathematics, 2006, 51(1), 73-88. doi: 10.1007/s10492-006-0006-x [8] G. Engel, K. Garikipati, T. Hughes, et al., Continuous/discontinuous finite element approximations of fourth-order elliptic problems in structural and continuum mechanics with applications to thin beams and plates, and strain gradient elasticity, Computer Methods in Applied Mechanics and Engineering, 2002, 191(34), 3669-3750. doi: 10.1016/S0045-7825(02)00286-4 [9] F. Haddouchi and N. Houari, Monotone positive solution of fourth order boundary value problem with mixed integral and multi-point boundary conditions, Journal of Applied Mathematics and Computing, 2021, 66, 87-109. doi: 10.1007/s12190-020-01426-4 [10] D. Kaur and R. K. Mohanty, Highly accurate compact difference scheme for fourth order parabolic equation with Dirichlet and Neumann boundary conditions: Application to good Boussinesq equation, Applied Mathematics and Computation, 2020, 378, 125202. doi: 10.1016/j.amc.2020.125202 [11] B. Li, G. Fairweather and B. Bialecki, Discrete-time orthogonal spline collocation methods for vibration problems, SIAM Journal on Numerical Analysis, 2002, 39, 2045-2065. doi: 10.1137/S0036142900348729 [12] L. Li and J. An, An efficient spectral method and rigorous error analysis based on dimension reduction scheme for fourth order problems, Numerical Methods for Partial Differential Equations, 2021, 37(1), 152-171. doi: 10.1002/num.22523 [13] Y. Ma and L. Chen, A Jacobi-Galerkin spectral method for computing the ground and first excited states of the nonlinear fractional Schrödinger equation, East Asian Journal on Applied Mathematics, 2020, 10(2), 274-294. doi: 10.4208/eajam.140319.180719 [14] M. Molina-Meyer and F. R. Prieto-Medina, Pseudospectral versus Galerkin methods: Fourth order equations, Journal of Computational and Applied Mathematics, 2022, 413, 114348. doi: 10.1016/j.cam.2022.114348 [15] J. Rappaz, B. Mercier, J. Osborn, et al., Eigenvalue approximation by mixed and hybrid methods, Mathematics of Computation, 1981, 36(154), 427-453. doi: 10.1090/S0025-5718-1981-0606505-9 [16] S. Ren, T. Tan and J. An, An efficient spectral-Galerkin approximation based on dimension reduction scheme for transmission eigenvalues in polar geometries, Computers and Mathematics with Applications, 2020, 80(5), 940-955. doi: 10.1016/j.camwa.2020.05.018 [17] J. Shen, Efficient spectral-Galerkin methods Ⅲ: Polar and cylindrical geometries, Journal on Scientific Computing, 1997, 18(6), 1583-1604. doi: 10.1137/S1064827595295301 [18] J. Shen, Efficient spectral-Galerkin methods Ⅳ. Spherical geometries, Journal on Scientific Computing, 1999, 20(4), 1438-1455. doi: 10.1137/S1064827597317028 [19] J. Shen and J. An, Spectral approximation to a transmission eigenvalue problem and its applications to an inverse problem, Computers and Mathematics with Applications, 2015, 69(10), 1132-1143. doi: 10.1016/j.camwa.2015.03.002 [20] J. Shen and T. Tang, Spectral Methods: Algorithms, Analysis and Applications, Science Press, 2006. [21] J. Shen, T. Tang and L. Wang, Spectral Methods: Algorithms, Analysis and Applications, Springer Science in Computational Mathematics, 2011, 41. Springer, Heidelberg. [22] J. Shen, L. Wang and H. Li, A triangular spectral element method using fully tensorial rational basis functions, Journal on Numerical Analysis, 2009, 47(3), 1619-1650. doi: 10.1137/070702023 [23] J. Shen, J. Xu and J. Yang, The scalar auxiliary variable (SAV) approach for gradient flows, Journal of Computational Physics, 2018, 353, 407-416. doi: 10.1016/j.jcp.2017.10.021 [24] J. Shen, J. Xu and J. Yang, A new class of efficient and robust energy stable schemes for gradient flows, SIAM Review, 2019, 61(3), 474-506. doi: 10.1137/17M1150153 [25] E. Shivanian and S. Abbasbandy, Pseudospectral meshless radial point interpolation for generalized biharmonic equation in the presence of Cahn-Hilliard conditions-, Computational and Applied Mathematics, 2020, 39, 1-18. doi: 10.1007/s40314-019-0964-8 [26] T. Tan, W. Cao and J. An, Spectral approximation based on a mixed scheme and its error estimates for transmission eigenvalue problems, Computers and Mathematics with Applications, 2022, 111, 20-33. doi: 10.1016/j.camwa.2022.02.009 [27] Y. Yang and W. Jiang, Upper spectral bounds and a posteriori error analysis of several mixed finite element approximations for the stokes eigenvalue problem, Science China Mathematics, 2013, 56(6), 1313-1330. doi: 10.1007/s11425-013-4582-4 [28] B. Zinsou, Asymptotics of the eigenvalues of self-adjoint fourth order boundary value problems, Differential Equations and Dynamical Systems, 2021, 1-22. -
-
Figures(12) / Tables(8)
Export File
Citation
Yuanlu Wang, Jiantao Jiang, Jing An. SPECTRAL-GALERKIN APPROXIMATION BASED ON REDUCED ORDER SCHEME FOR FOURTH ORDER EQUATION AND ITS EIGENVALUE PROBLEM WITH SIMPLY SUPPORTED PLATE BOUNDARY CONDITIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 61-83. doi: 10.11948/20230018
Format
Content
DownLoad:
-
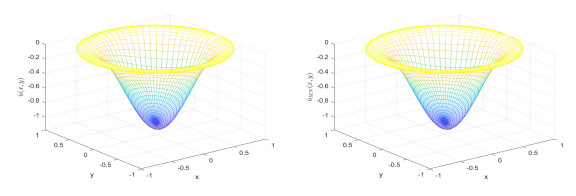
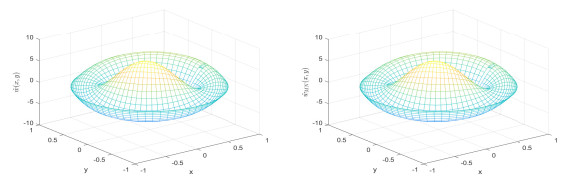
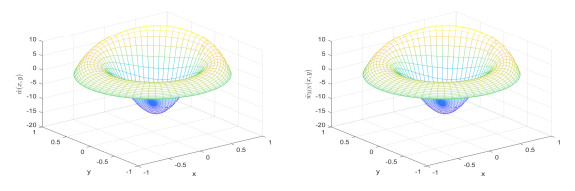
Figure 1.
Comparison figures of exact solutions (left) and approximation solutions (right) with
$ N = 30 $ $ M = 15 $ -
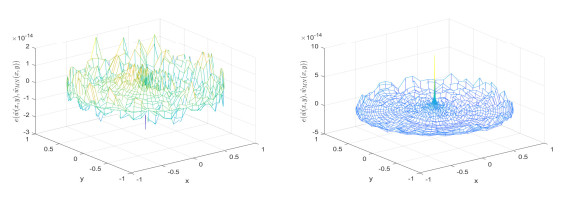
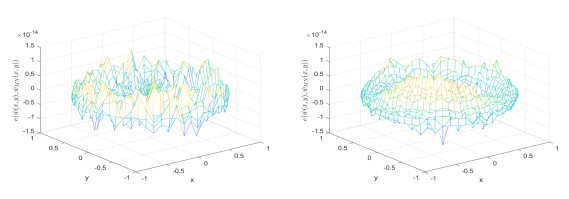
Figure 2.
The error figures of exact solutions
$ \hat{w}(x,y) $ $ \hat{w}_{MN}(x,y) $ $ N = 30 $ $ M = 14 $ $ N=45 $ $ M = 25 $ -
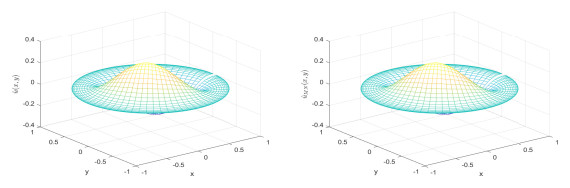
Figure 3.
Comparison figures of exact solutions (left) and approximation solutions (right) with
$ N = 35 $ $ M = 15 $ -
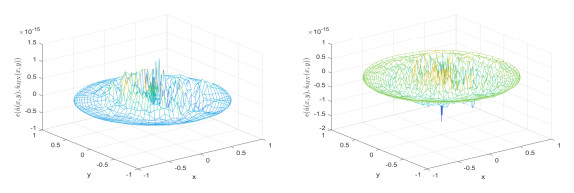
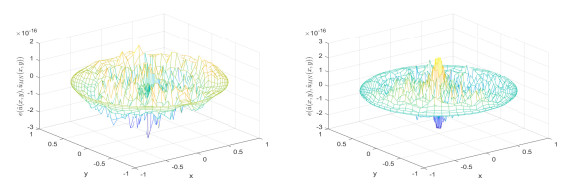
Figure 4.
The error figures of exact solutions
$ \hat{u}(x,y) $ $ \hat{u}_{MN}(x,y) $ $ N = 30 $ $ M = 15 $ $ N=45 $ $ M = 25 $ -
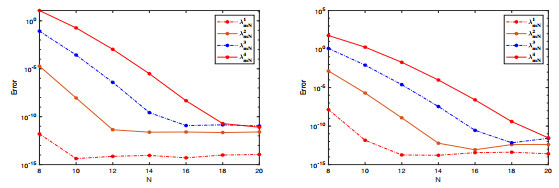
Figure 5.
Error curves between the numerical solutions
$ \hat{w}_{MN}(x,y) $ $ \hat{u}_{MN}(x,y) $ $ N $ $ M = 12 $ -
Figure 6.
Comparison figures of exact solutions (left) and approximation solutions (right) with
$ N = 35 $ $ M = 15 $ -
Figure 7.
The error figures of exact solutions
$ \hat{w}(x,y) $ $ \hat{w}_{MN}(x,y) $ $ N = 30 $ $ M = 14 $ $ N=35 $ $ M = 15 $ -
Figure 8.
Comparison figures of exact solutions (left) and approximation solutions (right) with
$ N = 35 $ $ M = 15 $ -
Figure 9.
The error figures of exact solutions
$ \hat{u}(x,y) $ $ \hat{u}_{MN}(x,y) $ $ N = 30 $ $ M = 14 $ $ N=40 $ $ M = 25 $ -
Figure 10.
The error tendency curves between numerical solutions and reference solutions with
$ m=0 $ $ m=1 $ -
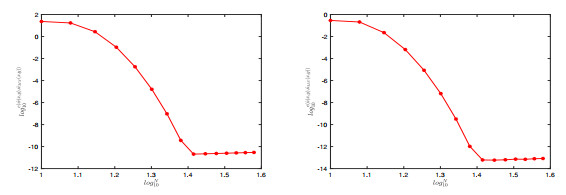
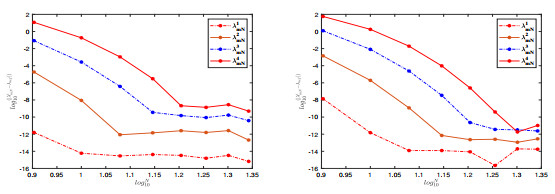
Figure 11.
Errors between the numerical solutions and the reference solutions on log-log scale with
$ m=0 $ $ m=1 $ -
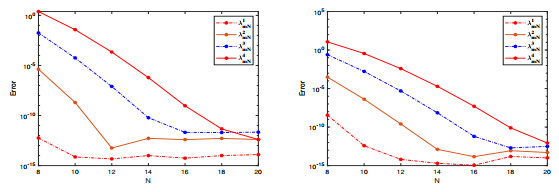
Figure 12.
The error tendency curves between numerical solutions and reference solutions with
$ m=0 $ $ m=1 $