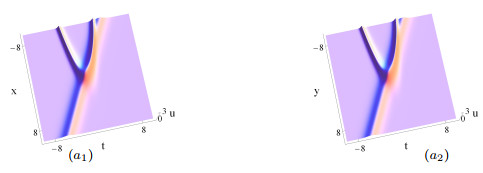| Citation: |
Yu-Qi Chen, Bo Tian, Qi-Xing Qu, Cheng-Cheng Wei, Dan-Yu Yang. PAINLEVÉ INTEGRABLE PROPERTY, BILINEAR FORM, BÄCKLUND TRANSFORMATION, KINK AND SOLITON SOLUTIONS OF A (2+1)-DIMENSIONAL VARIABLE-COEFFICIENT GENERAL COMBINED FOURTH-ORDER SOLITON EQUATION IN A FLUID OR PLASMA[J]. Journal of Applied Analysis & Computation, 2024, 14(2): 742-759. doi: 10.11948/20230056
|
PAINLEVÉ INTEGRABLE PROPERTY, BILINEAR FORM, BÄCKLUND TRANSFORMATION, KINK AND SOLITON SOLUTIONS OF A (2+1)-DIMENSIONAL VARIABLE-COEFFICIENT GENERAL COMBINED FOURTH-ORDER SOLITON EQUATION IN A FLUID OR PLASMA
-
Abstract
In this paper, we focus our attention on a (2+1)-dimensional variable-coefficient general combined fourth-order soliton equation in a fluid or plasma. Under certain coefficient constraints, we get the Painlevé integrable property. We obtain the bilinear form and bilinear auto-Bäcklund transformation. By virtue of the truncated Painlevé expansion, we derive an auto-Bäcklund transformation. Under certain coefficient constraints, we graphically analyse the one-kink waves, one soliton, two-kink waves and two solitons. We get the expressions of the amplitude and velocity of the one soliton and analyse the types of the two solitons and two-kink waves before and after the interactions.
-
-
References
[1] L. Akinyemi, Shallow ocean soliton and localized waves in extended (2+1)-dimensional nonlinear evolution equations, Phys. Lett. A, 2023, 463, 128668. doi: 10.1016/j.physleta.2023.128668 [2] M. B. Almatrafi and A. Alharbi, New soliton wave solutions to a nonlinear equation arising in plasma physics, CMES-Com. Model. Eng., 2023, 137(1), 1-15. [3] S. T. Chen and W. X. Ma, Lump solutions to a generalized Bogoyavlensky-Konopelchenko equation, Front. Math. China, 2018, 13, 525-534. doi: 10.1007/s11464-018-0694-z [4] Y. X. Chen, Soliton exotic collision of the (2+1)-dimensional modified dispersive water-wave system in fluid mechanics, Phys. Scr., 2020, 95(5), 055205. doi: 10.1088/1402-4896/ab66e0 [5] A. M. Elsherbeny, R. El-Barkouky, H. M. Ahmed, R. M. El-Hassani and A. H. Arnous, Travelling wave solutions for hierarchy of nonlinear evolution equation description propagation pulse in optical fibers, J. Optics, 2023, 52, 138-144. doi: 10.1007/s12596-022-00866-4 [6] X. Y. Gao, Considering the wave processes in oceanography, acoustics and hydrodynamics by means of an extended coupled (2+1)-dimensional Burgers system, Chin. J. Phys., 2023, 86, 572-577. doi: 10.1016/j.cjph.2023.10.051 [7] X. Y. Gao, Oceanic shallow-water investigations on a generalized Whitham-Broer-Kaup-Boussinesq-Kupershmidt system, Phys. Fluids, 2023, 35, 127106. doi: 10.1063/5.0170506 [8] S. Gugan, K. Subramanian, M. S. Mani Rajan and T. Alagesan, Four soliton propagation in a generalized nonautonomous Hirota equation using Darboux transformation, Opt. Quantum Electron., 2023, 55, 354. doi: 10.1007/s11082-023-04578-2 [9] H. D. Guo, T. C. Xia and B. B. Hu, High-order lumps, high-order breathers and hybrid solutions for an extended (3+1)-dimensional Jimbo-Miwa equation in fluid dynamics, Nonlinear Dyn., 2020, 100, 601-614. doi: 10.1007/s11071-020-05514-9 [10] R. Hirota, Direct Method in Soliton Theory, Springer, Berlin, 1980. [11] R. Hirota and J. Satsuma, Soliton solutions of a coupled Korteweg-de Vries equation, Phys. Lett. A, 1981, 85(8), 407-408. [12] J. Kalita, R. Das, K. Hosseini, D. Baleanu and S. Salahshour, Solitons in magnetized plasma with electron inertia under weakly relativistic effect, Nonlinear Dyn., 2023, 111, 3701-3711. doi: 10.1007/s11071-022-08015-z [13] J. Kaur, R. K. Gupta and S. Kumar, On explicit exact solutions and conservation laws for time fractional variable-coefficient coupled Burger's equations, Commun. Nonlinear Sci. Numer. Simulat., 2020, 83, 105108. doi: 10.1016/j.cnsns.2019.105108 [14] M. Kumar and A. K. Tiwari, Soliton solutions of BLMP equation by Lie symmetry approach, Comput. Math. Appl., 2018, 75(4), 1434-1442. doi: 10.1016/j.camwa.2017.11.018 [15] S. Kumar and B. Mohan, A direct symbolic computation of center-controlled rogue waves to a new Painlevé-integrable (3+1)-D generalized nonlinear evolution equation in plasmas, Nonlinear Dyn., 2023, 111, 16395-16405. doi: 10.1007/s11071-023-08683-5 [16] S. Kumar and B. Mohan, A generalized nonlinear fifth-order KdV-type equation with multiple soliton solutions: Painlevé analysis and Hirota Bilinear technique, Phys. Scr., 2022, 97(12), 125214. doi: 10.1088/1402-4896/aca2fa [17] S. Kumar and B. Mohan, A study of multi-soliton solutions, breather, lumps, and their interactions for kadomtsev-petviashvili equation with variable time coeffcient using hirota method, Phys. Scr., 2021, 96(12), 125255. doi: 10.1088/1402-4896/ac3879 [18] S. Kumar and B. Mohan, A novel and efficient method for obtaining Hirota's bilinear form for the nonlinear evolution equation in (n+1) dimensions, Partial Differ. Equ. Appl. Math., 2022, 5, 100274. doi: 10.1016/j.padiff.2022.100274 [19] S. Kumar, B. Mohan and R. Kumar, Newly formed center-controlled rouge wave and lump solutions of a generalized (3+1)-dimensional KdV-BBM equation via symbolic computation approach, Phys. Scr., 2023, 98, 085237. doi: 10.1088/1402-4896/ace862 [20] Z. Z. Lan, Y. T. Gao, J. W. Yang, C. Q. Su and Q. M. Wang, Solitons, Bäcklund transformation and Lax pair for a (2+1)-dimensional B-type Kadomtsev Petviashvili equation in the fluid/plasma mechanics, Commun. Nonlinear Sci. Numer. Simulat., 2016, 30, 1650265. [21] L. Li, C. Duan and F. Yu, An improved Hirota bilinear method and new application for a nonlocal integrable complex modified Korteweg-de Vries~(MKdV) equation, Phys. Lett. A, 2020, 383(14), 1578-1582. [22] Y. Liang, G. Wei and X. Li, Painlevé integrability, similarity reductions, new soliton and soliton-like similarity solutions for the (2+1)-dimensional BKP equation, Nonlinear Dyn., 2010, 62, 195-202. doi: 10.1007/s11071-010-9709-3 [23] F. Y. Liu and Y. T. Gao, Lie group analysis for a higher-order Boussinesq-Burgers system, Appl. Math. Lett., 2022, 132, 108094. doi: 10.1016/j.aml.2022.108094 [24] F. Y. Liu, Y. T. Gao, X. Yu and C. C. Ding, Wronskian, Gramian, Pfaffian and periodic-wave solutions for a (3+1)-dimensional generalized nonlinear evolution equation arising in the shallow water waves, Nonlinear Dyn., 2022, 108, 1599-1616. doi: 10.1007/s11071-022-07249-1 [25] J. G. Liu and W. P. Xiong, Multi-wave, breather wave and lump solutions of the Boiti-Leon-Manna-Pempinelli equation with variable coefficients, Results Phys., 2020, 19, 103532. doi: 10.1016/j.rinp.2020.103532 [26] M. S. Mani Rajan, Transition from bird to butterfly shaped nonautonomous soliton and soliton switching in erbium doped resonant fiber, Phys. Scr., 2020, 95, 105203. doi: 10.1088/1402-4896/abb2df [27] M. Mirzaei and S. M. Motevalli, Interaction of two soliton waves in plasma including electrons with Kappa-Cairns distribution function, Chin. J. Phys., 2023, 83, 347-353. doi: 10.1016/j.cjph.2022.08.002 [28] S. Saravana Veni and M. S. Mani Rajan, Attosecond soliton switching through the interactions of two and three solitons in an inhomogeneous fiber, Chaos Soliton Fract., 2021, 152, 11390. [29] S. Saravana Veni, S. Vijayalekshmi, R. Surekha and M. S. Mani Rajan, Non-collisional dynamics of nonautonomous three solitons through tailoring of modulated coefficients and modulation instability gain spectra, Optik, 2023, 279, 170737. doi: 10.1016/j.ijleo.2023.170737 [30] Y. Tang, S. Tao, M. Zhou and Q. Guan, Interaction solutions between lump and other solitons of two classes of nonlinear evolution equations, Nonlinear Dyn., 2017, 89, 429-442. doi: 10.1007/s11071-017-3462-9 [31] K. U. Tariq and R. Javed, Some traveling wave solutions to the generalized (3+1)-dimensional Korteweg-de Vries-Zakharov-Kuznetsov equation in plasma physics, Math. Method Appl. Scr., 2023, 46(12), 12200-12216. doi: 10.1002/mma.8596 [32] R. Udaiyakumar, N. Ben Ali, B. Mani Naicker, M. S. Mani Rajan, P. Yupapin and I. S. Amiri, Analytical and numerical demonstration of phase characteristics on two solitons under the influence of third-order dispersion, Opt. Quantum Electron., 2019, 51, 163. doi: 10.1007/s11082-019-1879-8 [33] S. Vijayalekshmi, A. Mahalingam, A. Uthayakumar and M. S. Mani Rajan, Oscillating soliton propagation in SPNLS equation with symmetric potentials, Optik, 2020, 221, 165143. doi: 10.1016/j.ijleo.2020.165143 [34] A. Vithya and M. S. Mani Rajan, Impact of fifth order dispersion on soliton solution for higher order NLS equation with variable coefficients, J. Ocean Eng. Sci., 2020, 5(3), 205-213. doi: 10.1016/j.joes.2019.11.002 [35] A. Vithya and M. M. Rajan, Impact of fifth order dispersion on soliton solution for higher order NLS equation with variable coefficients, J. Ocean Eng. Sci., 2020, 5(3), 205-213. doi: 10.1016/j.joes.2019.11.002 [36] M. Vlieg-Hulstman and W. D. Halford, Exact solutions to KdV equations with variable coefficients and/or nonuniformities, Comput. Math. Appl., 1995, 29(1), 39-47. doi: 10.1016/0898-1221(94)00205-Y [37] J. Y. Wang, Z. F. Liang and X. Y. Tang, Infinitely many generalized symmetries and Painlevé analysis of a (2+1)-dimensional Burgers system, Phys. Scr., 2014, 89(2), 025201. doi: 10.1088/0031-8949/89/02/025201 [38] X. H. Wu and Y. T. Gao, Generalized Darboux transformation and solitons for the Ablowitz-Ladik equation in an electrical lattice, Appl. Math. Lett., 2023, 137, 108476. doi: 10.1016/j.aml.2022.108476 [39] X. H. Wu, Y. T. Gao, X. Yu, L. Q. Li and C. C. Ding, Vector breathers, rogue and breather-rogue waves for a coupled mixed derivative nonlinear Schrödinger system in an optical fiber, Nonlinear Dyn., 2023, 111, 5641-5653. doi: 10.1007/s11071-022-08058-2 [40] J. Y. Yang, W. X. Ma and C. M. Khalique, Determining lump solutions for a combined soliton equation in (2+1)-dimensions, Eur. Phys. J. Plus, 2020, 135, 494. doi: 10.1140/epjp/s13360-020-00463-z [41] X. D. Yang and H. Y. Ruan, A Maple Package on Symbolic Computation of Hirota Bilinear Form for Nonlinear Equations, Commun. Theor. Phys., 2009, 52(5), 801. doi: 10.1088/0253-6102/52/5/07 [42] Y. Zhou, S. Manukure and W. X. Ma, Lump and lump-soliton solutions to the Hirota-Satsuma-Ito equation, Commun. Nonlinear Sci. Numer. Simulat., 2019, 68, 56-62. doi: 10.1016/j.cnsns.2018.07.038 [43] Z. J. Zhou, J. Z. Fu and Z. B. Li, Maple packages for computing Hirota's bilinear equation and multisoliton solutions of nonlinear evolution equations, Appl. Math. Comput., 2010, 217(1), 92-104. -
-
Figures(16)
Export File
Citation
Yu-Qi Chen, Bo Tian, Qi-Xing Qu, Cheng-Cheng Wei, Dan-Yu Yang. PAINLEVÉ INTEGRABLE PROPERTY, BILINEAR FORM, BÄCKLUND TRANSFORMATION, KINK AND SOLITON SOLUTIONS OF A (2+1)-DIMENSIONAL VARIABLE-COEFFICIENT GENERAL COMBINED FOURTH-ORDER SOLITON EQUATION IN A FLUID OR PLASMA[J]. Journal of Applied Analysis & Computation, 2024, 14(2): 742-759. doi: 10.11948/20230056
Format
Content
DownLoad:
-
Figure 1.
One kink wave via Solutions (4.5) under Coefficient Constraints (4.4), (
$ a_1-c_1 $ $ y $ $ a_2-c_2 $ $ x $ $ a_1 $ $ a_2 $ $ \delta_2(t) $ $ t-1 $ $ \delta_3(t) $ $ -t $ $ \delta_4(t) $ $ \alpha $ -
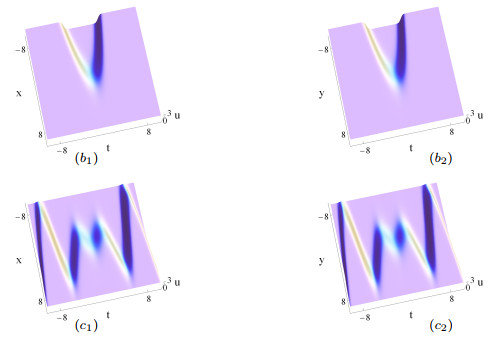
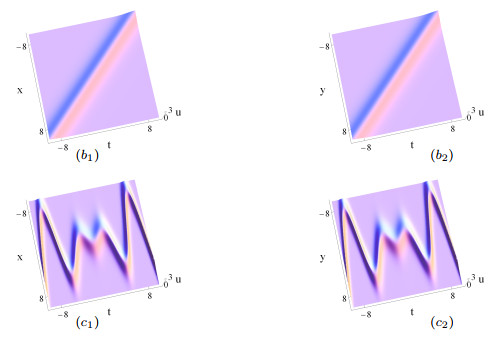
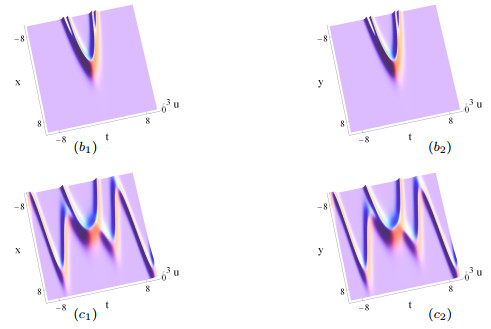
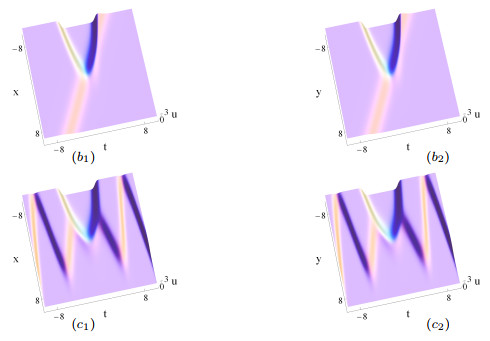
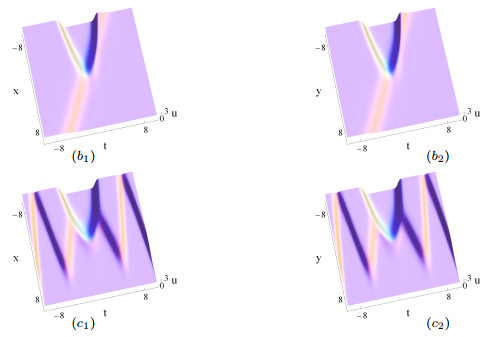
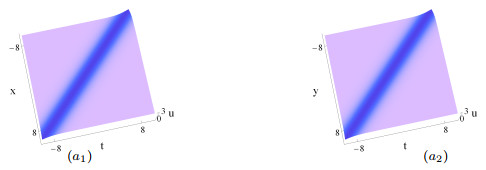
Figure 2.
The same as Figs. 1 (
$ a_1 $ $ a_2 $ $ b_1 $ $ b_2 $ $ \delta_2(t) $ $ 2t^2-1 $ $ c_1 $ $ c_2 $ $ \delta_2(t) $ $ t(\sin t+t\cos t)-1 $ -
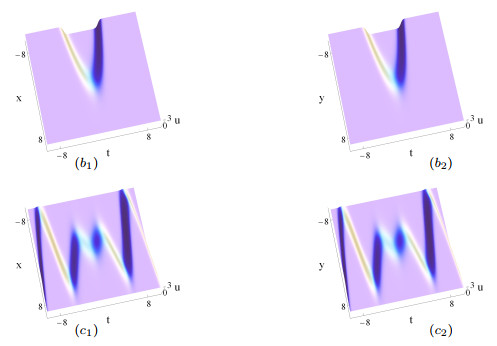
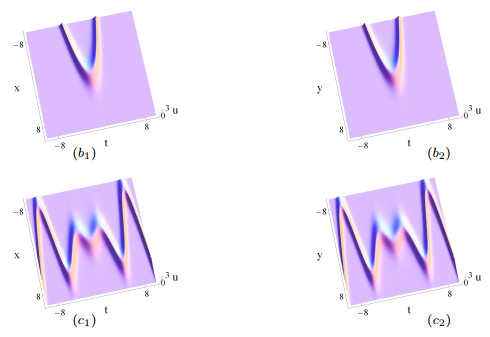
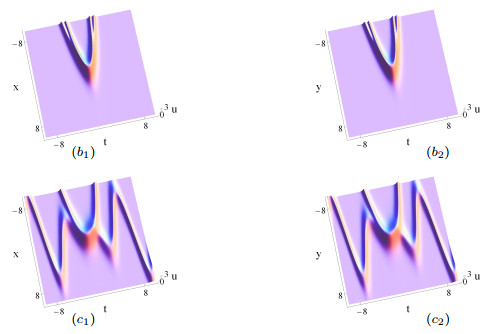
Figure 3.
The same as Figs. 1 (
$ a_1 $ $ a_2 $ $ b_1 $ $ b_2 $ $ \delta _3(t) $ $ -0.5 $ $ c_1 $ $ c_2 $ $ \delta_3(t) $ $ -\frac{t}{\sin t+t\cos t} $ -
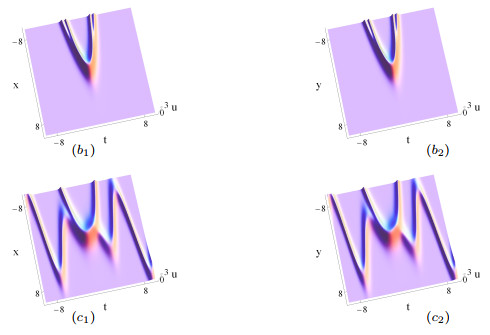
Figure 4.
The same as Figs. 1 (
$ a_1 $ $ a_2 $ $ b_1 $ $ b_2 $ $ \delta_4(t) $ $ 2t^2-1 $ $ c_1 $ $ c_2 $ $ \delta_4(t) $ $ t(\sin t+t\cos t)-1 $ -
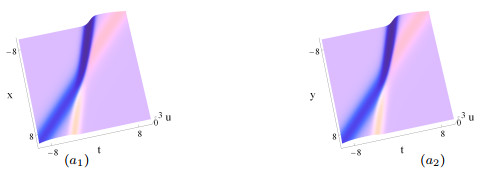
Figure 5.
One soliton via Solutions (5.3) under Coefficient Constraints (5.2), (
$ a_1-c_1 $ $ y=0 $ $ a_2-c_2 $ $ x=0 $ $ a_1 $ $ a_2 $ $ \delta_2(t) $ $ t $ $ \delta_1(t) $ $ 1 $ $ \delta_4(t) $ $ 1 $ $ \alpha $ $ 1 $ -
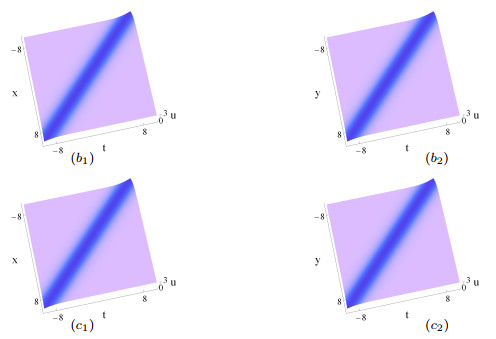
Figure 6.
The same as Figs. 5 (
$ a_1 $ $ a_2 $ $ b_1 $ $ b_2 $ $ \delta _1(t) $ $ t $ $ c_1 $ $ c_2 $ $ \delta_1(t) $ $ \sin t $ -
Figure 7.
The same as Figs. 5 (
$ a_1 $ $ a_2 $ $ b_1 $ $ b_2 $ $ \delta_2(t) $ $ 1 $ $ c_1 $ $ c_2 $ $ \delta_2(t) $ $ \sin t $ -
Figure 8.
The same as Figs. 5 (
$ a_1 $ $ a_2 $ $ b_1 $ $ b_2 $ $ \delta_4(t) $ $ t $ $ c_1 $ $ c_2 $ $ \delta_4(t) $ $ \sin t $ -
Figure 9.
Two solitons via Solutions (5.7) under Coefficient Constraints (5.6), (
$ a_1-c_1 $ $ y=0 $ $ a_2-c_2 $ $ x=0 $ $ a_1 $ $ a_2 $ $ \delta_4(t) $ $ 1 $ $ \alpha $ $ 1 $ $ \delta_1(t) $ $ 2 $ $ \delta_2(t) $ $ t $ -
Figure 10.
The same as Figs. 9 (
$ a_1 $ $ a_2 $ $ b_1 $ $ b_2 $ $ \delta_1(t) $ $ t $ $ \delta_2(t) $ $ 2t $ $ c_1 $ $ c_2 $ $ \delta_1(t) $ $ t $ $ \delta_2(t) $ $ \cos t $ -
Figure 11.
The same as Figs. 9 (
$ a_1 $ $ a_2 $ $ b_1 $ $ b_2 $ $ \delta_1(t) $ $ t $ $ \delta_4(t) $ $ 2t $ $ c_1 $ $ c_2 $ $ \delta_1(t) $ $ t $ $ \delta_4(t) $ $ \cos t $ -
Figure 12.
The same as Figs. 9 (
$ a_1 $ $ a_2 $ $ b_1 $ $ b_2 $ $ \delta_4(t) $ $ 2t $ $ c_1 $ $ c_2 $ $ \delta_4(t) $ $ \cos t $ -
Figure 13.
Two kink waves via Solutions (6.5) under Coefficient Constraints (6.4), (
$ a_1-c_1 $ $ y=0 $ $ a_2-c_2 $ $ x=0 $ $ a_1 $ $ a_2 $ $ \delta_4(t) $ $ 1 $ $ \alpha $ $ 1 $ $ \delta_1(t) $ $ 1 $ $ \delta_2(t) $ $ 3 $ -
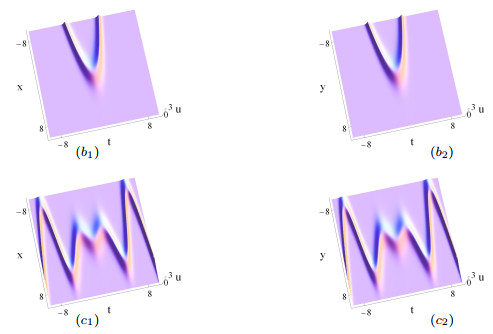
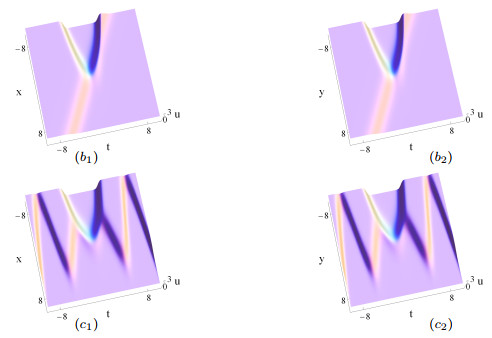
Figure 14.
The same as Figs. 13 (
$ a_1 $ $ a_2 $ $ b_1 $ $ b_2 $ $ \delta_1(t) $ $ t $ $ \delta_2(t) $ $ 2 $ $ c_1 $ $ c_2 $ $ \delta_1(t) $ $ t $ $ \delta_2(t) $ $ \sin t $ -
Figure 15.
The same as Figs. 13 (
$ a_1 $ $ a_2 $ $ b_1 $ $ b_2 $ $ \delta_1(t) $ $ t $ $ \delta_4(t) $ $ 2 $ $ c_1 $ $ c_2 $ $ \delta_1(t) $ $ t $ $ \delta_4(t) $ $ \sin t $ -
Figure 16.
The same as Figs. 13 (
$ a_1 $ $ a_2 $ $ b_1 $ $ b_2 $ $ \delta_2(t) $ $ t $ $ \delta_4(t) $ $ 2 $ $ c_1 $ $ c_2 $ $ \delta_2(t) $ $ t $ $ \delta_4(t) $ $ \sin t $