| Citation: |
Ai Ke, Jibin Li. EXACT SOLUTIONS AND DYNAMICS OF KUNDU-MUKHERJEE-NASKAR MODEL[J]. Journal of Applied Analysis & Computation, 2024, 14(2): 1014-1022. doi: 10.11948/20230265
|
EXACT SOLUTIONS AND DYNAMICS OF KUNDU-MUKHERJEE-NASKAR MODEL
-
Abstract
For the Kundu-Mukherjee-Naskar model, to find its exact explicit solutions, it is necessary to analyze the dynamical behaviors of the corresponding differential system of the amplitude component, which is a planar dynamical system with a singular straight line. In this paper, by using the techniques from dynamical systems to analyze the parameter conditions of system and find the corresponding phase portraits, the dynamical behaviors of the amplitude component can be derived. Under different parameter conditions, exact explicit homoclinic solutions, periodic solution families as well as kink and anti-kink wave solutions can be found.
-
-
References
[1] P. F. Byrd and M. D. Fridman, Handbook of Elliptic Integrals for Engineers and Scientists, Springer, Berlin, 1971. [2] R. Camassa and D. D. Holm, An integrable shallow water equation with peak solutions, Phys. Rev. Lett., 1993, 71(11), 1161–1164. [3] R. Camassa, J. M. Hyman and B. P. Luce, Nonlinear waves and solitons in physical sysytems, Phys. D, 1998, 123(1–4), 1–20. doi: 10.1016/S0167-2789(98)00108-0 [4] A. Degasperis, D. D. Holm and A. N. W. Hone, A new integrable equation with peakon solutions, Theoret. Math. Phys., 2002, 133(2), 1463–1474. doi: 10.1023/A:1021186408422 [5] A. Degasperis and M. Procesi, Asymptotic integrability, in: A. Degasperis, G. Gaeta(Eds. ), Symmetry and Perturbation Theory, World Scientific, Singapore, 1999, 23–37. [6] A. S. Fokas, On class of physically important integrable equations, Phys. D, 1995, 87, 145–150. doi: 10.1016/0167-2789(95)00133-O [7] J. Li, Singular Nonlinear Traveling Wave Equations: Bifurcations and Exact Solutions, Science Press, Beijing, 2013. [8] J. Li and G. Chen, On a class of singular nonlinear traveling wave equations, Int. J. Bifur. Chaos, 2007, 17(11), 4049–4065. doi: 10.1142/S0218127407019858 [9] J. Li and Z. Qiao, Peakon, pseudo-peakon, and cuspon solutions for two generalized Camassa-Holm equations, J. Math. Phys., 2013, 54, 123501. doi: 10.1063/1.4835395 [10] J. Li, W. Zhou and G. Chen, Understanding peakons, periodic peakons and compactons via a shallow water wave equation, Int. J. Bifur. Chaos, 2016, 26(12), 1650207. doi: 10.1142/S0218127416502072 [11] V. Novikov, Generalizations of the Camassa-Holm equation, J. Phys. A: Math. Theor., 2009, 42, 342002. doi: 10.1088/1751-8113/42/34/342002 [12] P. Olver and P. Rosenau, Tri-Hamiltonian duality between solitons and solitary-wave solutions having compact support, J. Phys. A: Math. Theor., 1996, 53(2), 1900–1906. [13] Z. Qiao, A new integrable equation with cuspons and W/M-shape-peaks solitons, J. of Mathematical Physics, 2006, 47, 112701. doi: 10.1063/1.2365758 [14] Z. Qiao, New integrable hierarchy, parametric solutions, cuspons, one-peak solitons, and M/W-shape peak solutions, J. of Mathematical Physics, 2007, 48, 082701. doi: 10.1063/1.2759830 [15] H. Triki, A. Benlallia, Q. Zhou, A. Biswasd, Y. Yıldırımh, A. Alzahranii and M. Belic, Gray optical dips of Kundu-Mukherjee-Naskar model, Phys. Lett. A, 2021, 401, 127341. doi: 10.1016/j.physleta.2021.127341 -
-
Figures(3)
Export File
Citation
Ai Ke, Jibin Li. EXACT SOLUTIONS AND DYNAMICS OF KUNDU-MUKHERJEE-NASKAR MODEL[J]. Journal of Applied Analysis & Computation, 2024, 14(2): 1014-1022. doi: 10.11948/20230265
Format
Content
DownLoad:
-
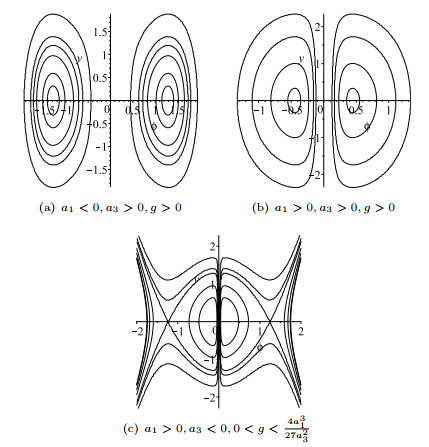
Figure 1.
The bifurcations of phase portraits of system (1.10).
-
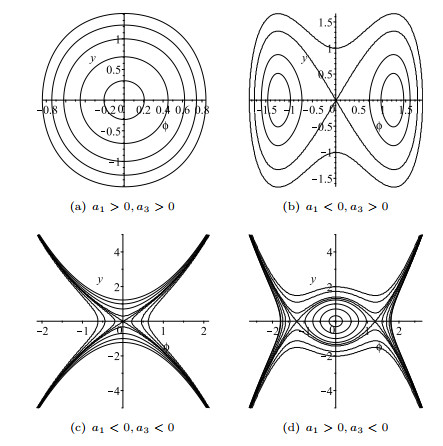
Figure 2.
The bifurcations of phase portraits of system (1.8).
-
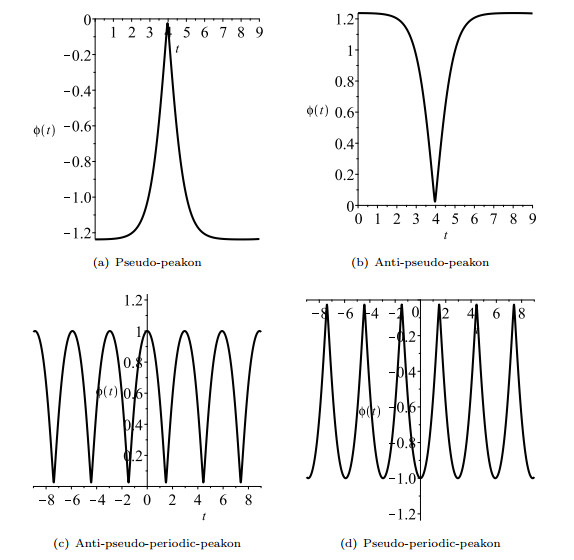
Figure 3.
The pseudo-peakon and pseudo-periodic peakon of system (1.8).