| Citation: |
H. I. Abdel-Gawad, B. Abdel-Aziz, M. Tantawy. EXTENDED CENTER MANIFOLD, GLOBAL BIFURCATION AND APPROXIMATE SOLUTIONS OF CHEN CHAOTIC DYNAMICAL SYSTEM[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2125-2139. doi: 10.11948/20230308
|
EXTENDED CENTER MANIFOLD, GLOBAL BIFURCATION AND APPROXIMATE SOLUTIONS OF CHEN CHAOTIC DYNAMICAL SYSTEM
-
Abstract
The study of the chaotic Chen dynamic System (CDS) has been a recent focus in the literature, with numerous works exploring its various chaotic features. However, the majority of these studies have relied primarily on numerical techniques to investigate nonlinear dynamic systems (NLDSs). In this context, our aim is to derive approximate analytical solutions for the CDS by developing an iterative scheme. We have proven the convergence theorem for this scheme, which ensures that our iterative process will converge to the exact solution. Additionally, we introduce a new method for constructing the extended center manifold, a critical component in the analysis of dynamical systems. The characteristics of the global bifurcation of the system components within the parameter space are explored. The error analysis of the iterated solutions demonstrates the efficiency of the present technique. We present both three-dimensional (3D) and two-dimensional (2D) phase portraits of the system. The 3D portrait reveals a feedback loop pattern, while the 2D portrait, which represents the interaction of the system components, exhibits multiple pools and cross pools. Furthermore, we illustrate the global bifurcation by visualizing the components of the CDS against the space-parameters. The sensitivity of CDS to infinitesimal variations in the initial conditions (ICs) is tested. It is found that even minor changes can lead to significant alterations in the system.
-
-
References
[1] H. I. Abdel-Gawad, Approximate-analytic optical soliton solutions of a modifed-Gerdjikov–Ivanov equation: Modulation instability, Opt. Quant. Elect., 2023, 55, 298. doi: 10.1007/s11082-023-04566-6 [2] H. I. Abdel-Gawad, M. Tantawy and A. M. Abdelwahab, Approximate solutions of fractional dynamical systems based on the invariant exponential functions with an application. A novel double-kernel fractional derivative, Alex. Eng. J., 2023, 77, 341–350. doi: 10.1016/j.aej.2023.06.044 [3] M. F. Alotaibi, N. Raza, M. H. Rafiq and A. Soltani, New solitary waves, bifurcation and chaotic patterns of Fokas system arising in monomode fiber communication system, Alex. Eng. J., 2023, 67, 583–595. doi: 10.1016/j.aej.2022.12.069 [4] M. Alqhtani, R. Srivastava, H. I. Abdel-Gawad, J. E. Macías-Díaz, K. M. Saad and W. M. Hamanah, Insight into functional Boiti–Leon–Mana–Pempinelli equation and error control: Approximate similarity solutions, Mathematics, 2023, 11(22), 4569. doi: 10.3390/math11224569 [5] V. Berinde, Picard iteration conver, ges faster than Mann iteration for a class of quasi-contractive operators, Fixed Point Theo. Applicat., 2004, 716359. [6] S. Bouali, A novel strange attractor with a stretched loop, Nonlinear Dyn., 2012, 70, 2375–2381. doi: 10.1007/s11071-012-0625-6 [7] S. Cang, G. Qi and Z. Chen, A four-wing hyper-chaotic attractor and transient chaos generated from a new 4-D quadratic autonomous system, Nonlinear Dyn., 2010, 59, 515–527. doi: 10.1007/s11071-009-9558-0 [8] S. Cang, L. Wang, Y. Zhang, Z. Wang and Z. Chen, Bifurcation and chaos in a smooth 3D dynamical system extended from Nosé-Hoover oscillator, Chaos Solitons Fractals, 2022, 158, 112016. doi: 10.1016/j.chaos.2022.112016 [9] M. D. Chekroun, Il. Koren and H. Liu, Efficient reduction for diagnosing Hopf bifurcation in delay differential systems: Applications to cloud-rain models, Chaos, 2020, 30, 053130. doi: 10.1063/5.0004697 [10] K. Dekker and J. G. Verwer, Stability of Runge–Kutta Methods for Stiff Nonlinear Differential Equations, North-Holland, Amsterdam, 1984. [11] K. Fallahi, R. Raoufi and H. Khoshbin, An application of Chen system for secure chaotic communication based on extended Kalman filter and multi-shift cipher algorithm, Commun. Nonl. Sci. Numer. Simul., 2008, 13(4), 763–781. doi: 10.1016/j.cnsns.2006.07.006 [12] V. R. Folifack Signing, G. A. Gakam Tegue, M. Kountchou, Z. T. Njitacke, N. Tsafack, J. D. D. Nkapkop, C. M. Lessouga Etoundi and J. Kengne, A cryptosystem based on a chameleon chaotic system and dynamic DNA coding, Chaos Solitons Fractals, 2022, 155, 111777. doi: 10.1016/j.chaos.2021.111777 [13] C. Gissinger, A new deterministic model for chaotic reversals, Eur. Phys. J. B, 2012, 85, 137–148. doi: 10.1140/epjb/e2012-20799-5 [14] A. S. Gonchenko and S. V. Gonchenko, Variety of strange pseudohy perbolic attractors in three-dimensional generalized Hénon maps, Physica D Nonl. Pheno., 2016, 337(15), 43–57. [15] S. Guo and S. Yan, Hopf bifurcation in a diffusive Lotka–Volterra type system with nonlocal delay effect, J. Diff. Eqs., 2016, 260(1), 781–817. doi: 10.1016/j.jde.2015.09.031 [16] M. Han, J. Llibre and Y. Tian, On the Zero-Hopf Bifurcation of the Lotka–Volterra Systems in R3, Mathematics, 2020, 8(7), 1137. doi: 10.3390/math8071137 [17] G.-D. Hu and Mingzhu Liu, The weighted logarithmic matrix normand bounds of the matrix exponential, Lie Algebra Appli., 2004, 390, 145–154. doi: 10.1016/j.laa.2004.04.015 [18] T. Kohda and K. Aihara, Chaos in discrete systems and diagnosis of experimental chaos, EICE Trams., 1990, E73(6), 772–783. [19] O. Leon, L. Kocaev, K. Eckert and M. Itoh, Experimental chaos synchronization in Chua's circuit, Int. J. Bifurcation Chaos, 1992, 02(03), 705–708. doi: 10.1142/S0218127492000811 [20] Y. Lin, C. Wang, H. He and L. L. Zhou, A novel four-wing non-equilibrium chaotic system and its circuit implementation, Paramana, 2016, 86(4), 801–807. doi: 10.1007/s12043-015-1118-1 [21] E. N. Lorenz, Deterministic nonperiodic flow, J. Atmos. Sci., 1963, 20(2), 130–140. doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 [22] J. Lü, G. Chen, D. Cheng and S. Celikovsky, Bridge the gap between the Lorenz system and the Chen system, Int. J. Bifurcation and Chaos, 2002, 12(12), 2917–2926. doi: 10.1142/S021812740200631X [23] M. Mossa Al-Sawalha and M. S. M. Noorani, A numeric–analytic method for approximating the chaotic Chen system, Chaos, Solitons and Fractals, 2009, 42, 1784–1791. doi: 10.1016/j.chaos.2009.03.096 [24] V. T. Pham, C. Volos, S. Jafari and T. Kapitaniak, Coexistence of hidden chaotic attractors in a novel no-equilibrium system, Nonlinear Dyn., 2017, 87, 2001–2010. doi: 10.1007/s11071-016-3170-x [25] V.-T. Pham, X. Wang, S. Jafari, C. Volos and T. Kapitaniak, From Wang–Chen system with only one stable equilibrium to a new chaotic system without equilibrium, Int. J. Bifurcation and Chaos, 2017, 27(6), 1750097. doi: 10.1142/S0218127417500973 [26] E. Ponce, J. Ros and F. Torres, On the fold-Hopf bifurcation for continuous piecewise linear differential systems with symmetry Jaume Llibre, Chaos, 2010, 20, 033119. doi: 10.1063/1.3486073 [27] Y. Ren, B. Zhang and H. Qiao, A simple Taylor-series expansion method for a class of second kind integral equations, J. Comput. Appl. Math., 1999, 110(1), 15–24. doi: 10.1016/S0377-0427(99)00192-2 [28] O. E. Rossler, Different types of chaos in two simple differential equations, Z. Naturforsch, 1976, 31, 1664–1670. doi: 10.1515/zna-1976-1231 [29] D. Ruelle, Chaotic Evolution and Strange Attractors, Cambridge University Press, 1989. [30] D. A. Russell, J. D. Hanson and E. Ott, Dimension of strange attractors, Phys. Rev. Lett., 1980, 45, 1175. doi: 10.1103/PhysRevLett.45.1175 [31] A. A. Śliwiak, N. Chandramoorthy and Q. Wang, Computational assessment of smooth and rough parameter dependence of statistics in chaotic dynamical systems, Commun. Nonl. Sci. Numer. Simul., 2021, 101, 105906. doi: 10.1016/j.cnsns.2021.105906 [32] H. Su and J. Xu, Time-delayed sampled-data feedback control of differential systems undergoing hopf bifurcation, Int. J. Bifur. Chaos, 2021, 31(01), 2150004. doi: 10.1142/S0218127421500048 [33] H. S. Tang, R. D. Haynes and G. Houzeaux, A review of domain decomposition methods for simulation of fluid flows: Concepts, algorithms, and applications, Arch. Comput. Meth. Eng., 2021, 28, 841–873. doi: 10.1007/s11831-019-09394-0 [34] Y. Tian and P. Yu, An explicit recursive formula for computing the formal form and center manifold for n-dimensional differential systems associated with hopf bifurcation, Int. J. Bifur Chaos, 2013, 23(06), 1350104. doi: 10.1142/S0218127413501046 [35] C. C. Tisdell, On Picard's iteration method to solve differential equations and a pedagogical space for otherness, Int. J. Math. Edu. Sci. Tech., 2019, 50(5), 788–799. doi: 10.1080/0020739X.2018.1507051 [36] N. B Tullaro, T. Abbott and J. P. Reil, An Experimental Approach to Nonlinear Dynamics and Chaos, Addison Wesley, 1992. [37] M. Yassen, The optimal control of Chen chaotic dynamical system, Appl. Math. Comput., 2002, 131(1), 171–180. [38] M. T. Yassen, Chaos control of Chen chaotic dynamical system, Chaos Solitons Fractals, 2003, 15(2), 271–283. [39] M. Zaid Odibat, A study on the convergence of variational iteration method, Math. Comput. Model., 2010, 51(9), 1181–1192. [40] T. Zhou and Y. Tang, Complex dynamical behaviors of the chaotic Chen's system, Int. J. Bifurcation and Chaos, 2003, 13(9), 2561–2574. -
-
Figures(5) / Tables(1)
Export File
Citation
H. I. Abdel-Gawad, B. Abdel-Aziz, M. Tantawy. EXTENDED CENTER MANIFOLD, GLOBAL BIFURCATION AND APPROXIMATE SOLUTIONS OF CHEN CHAOTIC DYNAMICAL SYSTEM[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2125-2139. doi: 10.11948/20230308
Format
Content
DownLoad:
-
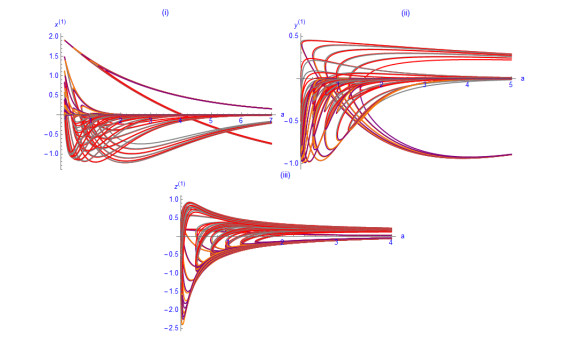
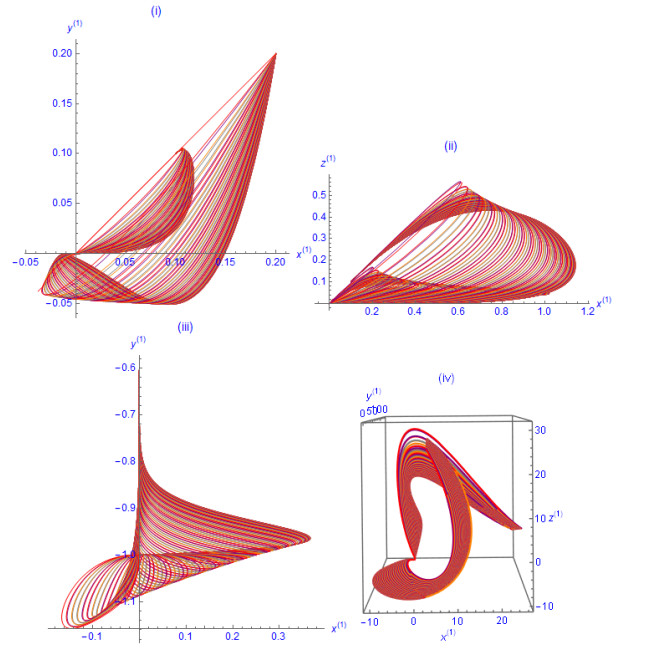
Figure 1.
(ⅰ)-(ⅴ). The phase portraits (2D-parametricplot) for each pair of
$ x^{(1)}, y^{(1)}, $ $ z^{(1)} $ $ a\text{=}2, \ b\text{=}0.1, \ x_{0}\text{=}0.1, \ y_{0}\text{=}0.2, \ z_{0}\text{=}0.8 $ -
Figure 2.
(ⅰ)-(ⅲ). Show the bifurcations of
$ x^{(1)}y^{(1)}, \boldsymbol{z}^{(1)} $ $ a $ $ b=0.1, \ x_{0}=2, \ y_{0}=-5, \ z_{0}=0.1 $ -
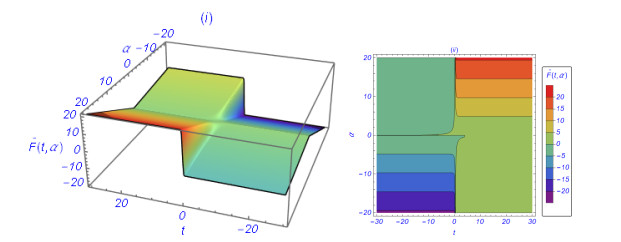
Figure 3.
(ⅰ), (ⅱ), show 3D and contour plot of Eq. (5.12), against
$ (t, \alpha $ -
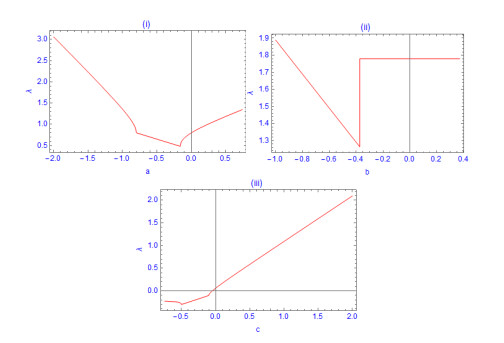
Figure 4.
(ⅰ) - (ⅱ). When: (ⅰ)
$ b=1.5, \ x_{0}=2, \ y_{0}=1.2, \ z_{0}=3, $ $ a\text{=}0.5, $ $ \nu\text{=}-0.2, \ \mu\text{=}0.19, \ x_{0}=2.5, \ y_{0}=1.5, \ z_{0}=3 $ $ a $ $ b $ $ c<0 $ $ c>0 $ -
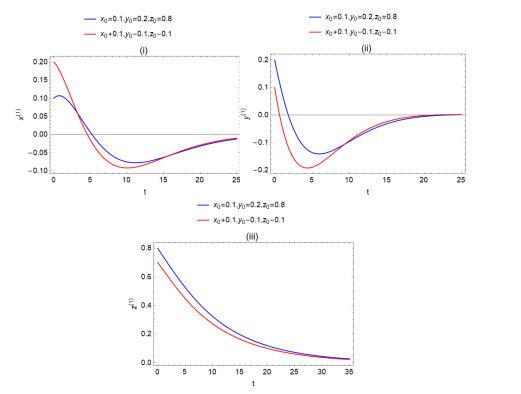
Figure 5.
(ⅰ). When
$ a=2, \ b=0.1, \ m=0.2, $