| Citation: | Yadong Shang, Huafei Di. BÄCKLUND TRANSFORMATIONS AND INFINITE NEW EXPLICIT EXACT SOLUTIONS OF A VARIANT BOUSSINESQ EQUATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2140-2157. doi: 10.11948/20230320 |
BÄCKLUND TRANSFORMATIONS AND INFINITE NEW EXPLICIT EXACT SOLUTIONS OF A VARIANT BOUSSINESQ EQUATIONS
-
Abstract
This paper deals with a variant Boussinesq equations which describes the propagation of shallow water waves in a lake or near an ocean beach. We derive out two hetero-Bäcklund transformations between the variant Boussinesq equations and two linear parabolic equations by using the extended homogeneous balance method. We also obtain two hetero-Bäcklund transformations between the variant Boussinesq equations and Burgers equations. Furthermore, we obtain two hetero-Bäcklund transformation between the variant Boussinesq equations and heat equations. By using these Bäcklund transformations and so-called "seed solution", we obtain a large number of explicit exact solutions of the variant Boussinesq equations. Especially, The infinite explicit exact singular wave solutions of variant Boussinesq equations are obtained for the first time. It is worth noting that these singular wave solutions of variant Boussinesq equations will blow up on some lines or curves in the (x, t) plane. These facts reflect the complexity of the structure of the solution of variant Boussinesq equations. It also reflects the complexity of shallow water wave propagation from one aspect.
-

-
References
[1] M. J. Ablowitz and P. A. Clarkson, Solitons, Nonlinear Evolution Equations and Inverse Scattering, Cambridge University Press, 1991. [2] L. Akinyemia, M. Senolb and O. S. Iyiola, Exact solutions of the generalized multidimensional mathematical physics models via sub-equation method, Math. Comput. Simula., 2021, 182, 211–233. doi: 10.1016/j.matcom.2020.10.017 [3] G. Arindam and M. Sarit, The first integral method and some nonlinear models, Comput. Appl. Math., 2021, 40, 79, 16 pp. [4] D. J. Arrigo, P. Broadbridge and J. M. Hill, Non-classical symmetry solutions and the methods of Bluman-Cole and Clarkson-Kruskal, J. Math. Phys., 1993, 34, 4692–4703. doi: 10.1063/1.530365 [5] B. Bibekananda, M. Hemanta and Z. D. Dia, Exact solution of the time fractional variant Boussinesq-Burgers equations, Appl. Math., 2021, 66(3), 437–449. doi: 10.21136/AM.2021.0269-19 [6] L. J. F. Broer, Approximate equations for long water waves, Appl. Sci. Res., 1975, 31(5), 377–395. doi: 10.1007/BF00418048 [7] D. Evgueni, Travelling waves in the Boussinesq type systems, J. Math. Pures Appl., 2022, 163(9), 1–10. [8] E. G. Fan, Two new applications of the homogeneous balance method, Phys. Lett. A, 2000, 265, 353–357. doi: 10.1016/S0375-9601(00)00010-4 [9] E. G. Fan and Y. C. Hon, A series of travelling wave solutions for two variant Boussinesq equations in shallow water waves, Chaos, Solitons and Fractals., 2003, 15, 559–566. doi: 10.1016/S0960-0779(02)00144-3 [10] E. G. Fan and H. Q. Zhang, A new approach to Bäcklund transformations of nonlinear evolution equations, Appl. Math. Mech., 1998, 19(7), 645–650. doi: 10.1007/BF02452372 [11] E. G. Fan and H. Q. Zhang, Bäcklund transformation and exact solutions for Whitham-Broer-Kaup equations in shallow water, Appl. Math. Mech., 1998, 19(8), 713–716. doi: 10.1007/BF02457745 [12] E. G. Fan and H. Q. Zhang, Symmetry reductions and similarity solutions of variant Boussinesq equation systems, (Chinese) Acta. Math. Sci., 1999, 19(4), 373–378. [13] B. L. Guo, Nonlinear Evolution Equations, Shanghai Scientific and Technological Education Publishing House, Shanghai, 1995. [14] H. Guo, T. Z. Xu, S. J. Yang and G. W. Wang, Aanlytical study of solitons for the variant Boussinesq equations, Nonliinear Dyn., 2017, 88, 1139–1146. doi: 10.1007/s11071-016-3300-5 [15] S. Hood, New exact solutions of Burgers's equation-an extension to the directmethod of Clarkson and Kruskal, J. Math. Phys., 1995, 36, 1971–1990. doi: 10.1063/1.531097 [16] D. J. Kaup, A higher-order water wave equation and the method for solving it, Prog. Theor. Phys., 1975, 54(2), 396–408. doi: 10.1143/PTP.54.396 [17] B. A. Kupershmidt, Mathematics of dispersive water waves, Commun. Math. Phys., 1985, 99, 51–73. doi: 10.1007/BF01466593 [18] W. H. Liu and Z. F. Zhang, Lie symmetry analysis, analytical solutions and conservation laws to the coupled time fractional variant Boussinesq equations, Waves Random Complex Media, 2021, 31(1), 182–197. doi: 10.1080/17455030.2019.1577583 [19] R. Naz, F. Mahomed and T. Hayat, Conservation laws for the third-order variant Boussinesq system, App. Math. Lett., 2010, 23(8), 8830886. [20] J. E. Okeke, R. Narain and K. S. Govinder, New exact solutions of a generalised Boussinesq equation with damping term and a system of variant Boussinesq equations via double reduction theory, J. Appl. Anal. Comp., 2018, 8(2), 471–485. [21] R. L. Sachs, On the integrable variant of the Boussinesq system: Painlevé property, rational solutions, a related many-body system, and equivalence with the AKNS hierarchy, Phys. D., 1988, 30(1–2), 1–27. [22] M. Sarit, G. Arindam and R. C. Asesh, Exact solutions and symmetry analysis of a new equation invariant under scaling of dependent variable, Phys. Scr., 2019, 94(8), 085212, 7 pp. [23] M. Sarit, G. Arindam and R. C. Asesh, Exact solutions and symmetry snalysis of a Boussinesq type equation for longitudinal waves through a magneto-electro-elastic circular rod, Int. J. Appl. Comput. Math., 2021, 7, 171, 14 pp. [24] M. L. Wang, Solitray wave solutions for variant Boussinesq equations, Phys. Lett. A, 1995, 199, 169–172. doi: 10.1016/0375-9601(95)00092-H [25] Z. Y. Yan and H. Q. Zhang, New explicit and exact travelling wave solutions for a system of variant Boussinesq equations in mathematical physics, Phys. Lett. A, 1999, 252(6), 291–296. doi: 10.1016/S0375-9601(98)00956-6 [26] Z. Y. Yan and H. Q. Zhang, New explicit solitary wave solutions and periodic wave solutions for Whitham-Broer-Kaup equation in shallow water, Phys. Lett. A, 2001, 285, 355–362. doi: 10.1016/S0375-9601(01)00376-0 [27] X. F. Yang, Z. C. Deng, Q. J. Li and Y. Wei, Exact combined traveling wave solutions and multi-sympletic structure of the varianr Boussinesq Whitham-Broer-Kaup type equations, Commun. Nonlin. Sci. Simul., 2016, 36, 1–13. doi: 10.1016/j.cnsns.2015.11.015 [28] E. Yomba, The extended Fan's sub-equation method and its application to KdV-MKdV, BKK, and variant Boussinesq equations, Phys. Lett. A, 2005, 336, 463–476. doi: 10.1016/j.physleta.2005.01.027 [29] Y. B. Yuan, D. M. Pu and S. M. Li, Bifurcations of travelling wave solutions in variant Boussinesq equations, Appl. Math. Mech., 2006, 27(7), 811–822. [30] J. F. Zhang, Multi-solitary wave solutions for variant Boussinesq equations and Kupershmidt equations, Appl. Math. Mech., 2000, 21(2), 193–198. [31] P. Zhang, New exact solutions to breaking soliton equations and Whitham-Broer-Kaup equations, Appl. Math. Comput., 2010, 217, 1688–1696. [32] W. G. Zhang, Q. Liu, X. Li and B. L. Guo, Shape analysis of bounded traveling wave solutions and solution to the generalized Whitham-Broer-Kaup equation with dissipation terms, Chin. Ann. Math., 2012, 33B(2), 281–308. [33] W. G. Zhang, Q. Liu, Z. M. Li and X. Li, Bounded traveling wave solutions of variant Boussinesq equation with a dissipation term and dissipation effect, Acta Math. Sci., 2014, 34B(3), 941–959. -
-
-
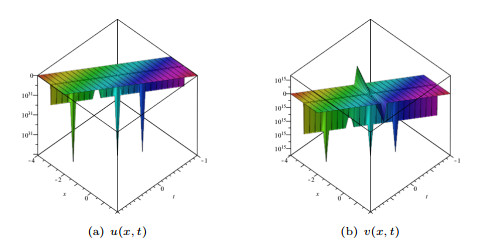
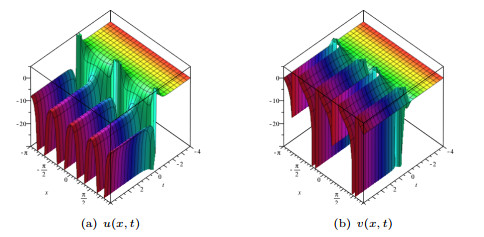
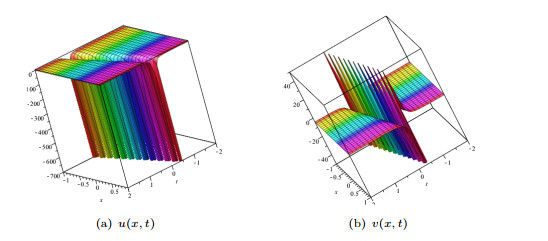
Figure 1.
The surface plots of (3.3) when
$C_1=1$ $C_2=-1$ -
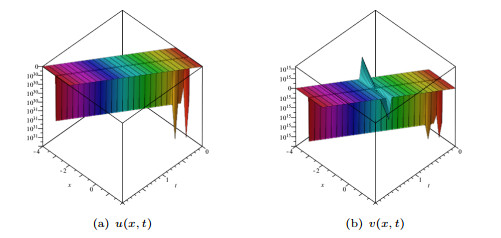
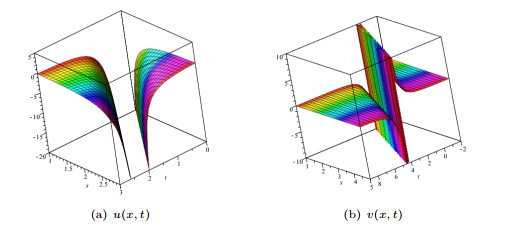
Figure 2.
The surface plots of (3.5) when
$c_1=1$ $c_2=0$ $\lambda_3=2$ -
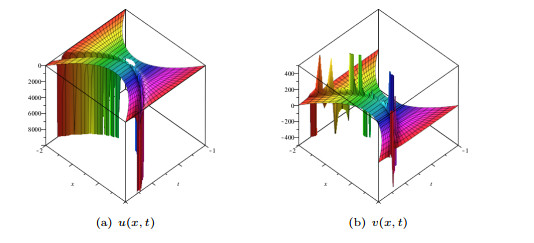
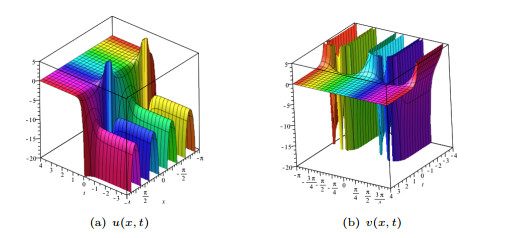
Figure 3.
The surface plots of (3.5) when
$c_1=1$ $c_2=-1$ $\lambda_3=c_3=2$ -
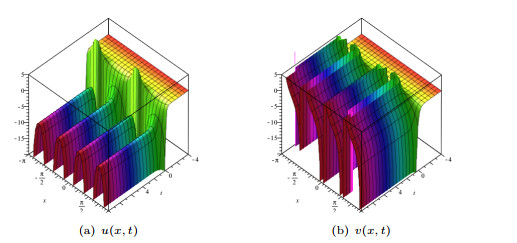
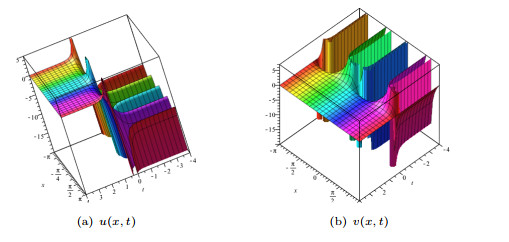
Figure 4.
The surface plots of (3.7) when
$a=b=c=1$ -
Figure 5.
The surface plots of (3.12) when
$A=1$ $B=-1$ $\lambda=2$ -
Figure 6.
The surface plots of (3.14) when
$A=-1$ $B=2$ $\lambda=-2$ -
Figure 7.
The surface plots of (3.16) when
$A=2$ $B=-1$ $k=1$ -
Figure 8.
The surface plots of (3.17) when
$A=1$ $B=-1$ $\lambda=2$ -
Figure 9.
The surface plots of (3.19) when
$A=-1$ $B=2$ $\lambda=-2$ -
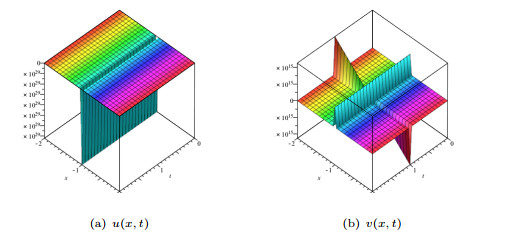
Figure 10.
The surface plots of (3.21) when
$A=3$ $B=-2$ $k=2$ -
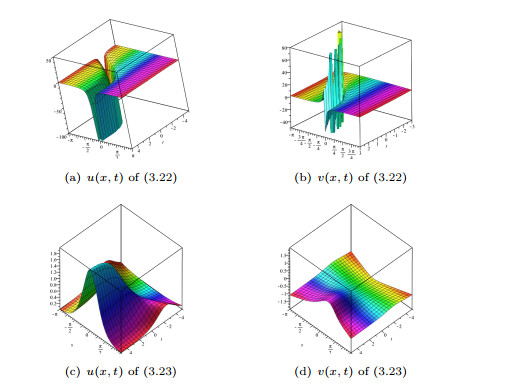
Figure 11.
The surface plots of (3.22) and (3.23) when
$A=B=\lambda=1$




 DownLoad:
DownLoad: