| Citation: | Ying Chen, Lihong Huang, Jiafu Wang. GLOBAL ASYMPTOTICAL STABILITY FOR A FISHERY MODEL WITH SEASONAL HARVESTING[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2196-2206. doi: 10.11948/20230354 |
GLOBAL ASYMPTOTICAL STABILITY FOR A FISHERY MODEL WITH SEASONAL HARVESTING
-
Abstract
A new fishery model is proposed by using the strategy of seasonal harvesting. Sufficient and necessary conditions are established to ensure the existence of a unique equilibrium or a periodic solution by the approach of Poincaré maps. It is shown that the equilibrium or the periodic solution is globally asymptotically stable. Numerical examples are provided to demonstrate the model dynamics and some biological implications are given as well.
-
Keywords:
- Seasonal harvesting /
- fishery model /
- Poincaré map /
- periodic solution /
- global stability
-

-
References
[1] P. M. Allen and J. M. McGlade, Dynamics of discovery and exploitation: The case of the scotian shelf groundfish fisheries, Can. J. Fish. Aquat. Sci., 1986, 43(6), 1187–1200. doi: 10.1139/f86-148 [2] R. Chinnathambi and F. Rihan, Analysis and control of Aedes Aegypti mosquitoes using sterile-insect techniques with Wolbachia, Math. Biosci. Eng., 2022, 19(11), 11154–11171. doi: 10.3934/mbe.2022520 [3] R. Cristiano, M. Henao and D. Pagano, Global stability of a Lotka-Volterra piecewise-smooth system with harvesting actions and two predators competing for one prey, J. Math. Anal. Appl., 2023, 522(2), 126998. doi: 10.1016/j.jmaa.2023.126998 [4] A. F. Filippov, Differential Equations with Discontinuous Right-hand Sides, Kluwer Academic Publishers, 1988. [5] E. Freire, E. Ponce and F. Torres, Canonical discontinuous planar piecewise linear systems, SIAM J. Appl. Dyn. Syst., 2012, 11(1), 181–211. doi: 10.1137/11083928X [6] M. Guardia, T. Seara and M. Teixeira, Generic bifurcations of low codimension of planar Filippov systems, J. Diff. Eqs., 2011, 250(4), 1967–2023. doi: 10.1016/j.jde.2010.11.016 [7] Z. Guo and X. Zou, Impact of discontinuous harvesting on fishery dynamics in a stock-effort fishing model, Commun. Nonlinear Sci. Numer. Simul., 2015, 20(2), 594–603. doi: 10.1016/j.cnsns.2014.06.014 [8] J. He and K. Wang, The survival analysis for a single-species population model in a polluted environment, Appl. Math. Model., 2007, 31(10), 2227–2238. doi: 10.1016/j.apm.2006.08.017 [9] D. Hu, Y. Zhang, Z. Zheng and M. Liu, Dynamics of a delayed predator-prey model with constant-yield prey harvesting, J. Appl. Anal. Comput., 2022, 12(1), 302–335. [10] L. Huang, Z. Guo and J. Wang, Theory and Applications of Differential Equtions with Discontinuous Right Hand Sides, Science Press, Beijing, 2011. [11] L. Huang and J. Wang, Models Described by Differential Equtions with Discontinuous Right Hand Sides and Their Dynamics, Science Press, Beijing, 2021. [12] Y. A. Kuznetsov, S. Rinaldi and A. Gragnani, One-parameter bifurcations in planar Filippov systems, Internat. J. Bifur. Chaos, 2003, 13(8), 2157–2188. doi: 10.1142/S0218127403007874 [13] W. Li, J. Ji and L. Huang, Global dynamic behavior of a predator–prey model under ratio-dependent state impulsive control, Appl. Math. Model., 2020, 77, 1842–1859. doi: 10.1016/j.apm.2019.09.033 [14] J. Liang, Y. Zhu, C. Xiang and S. Tang, Travelling waves and paradoxical effects in a discrete-time growth-dispersal model, Appl. Math. Model., 2018, 59, 132–146. doi: 10.1016/j.apm.2018.01.039 [15] P. Liu, J. Shi and Y. Wang, Periodic solutions of a logistic type population model with harvesting, J. Math. Anal. Appl., 2010, 369(2), 730–735. doi: 10.1016/j.jmaa.2010.04.027 [16] S. Liu and M. Han, Limit cycle bifurcations near double homoclinic and double heteroclinic loops in piecewise smooth systems, Chaos Solitons Fractals, 2023, 175, 113970. doi: 10.1016/j.chaos.2023.113970 [17] Y. Liu, J. Yu and J. Li, Global dynamics of a competitive system with seasonal succession and different harvesting strategies, J. Diff. Eqs., 2024, 382, 211–245. doi: 10.1016/j.jde.2023.11.024 [18] M. Schaefer, Some aspects of the dynamics of populations important to the management of the commercial marine fisheries, Bull. Math. Biol., 1991, 53(1–2), 253–279. doi: 10.1016/S0092-8240(05)80049-7 [19] J. Suh, H. Kwon and J. Lee, A model of Plasmodium vivax malaria with delays: Mathematical analysis and numerical simulations, Math. Comput. Simul., 2024, 217, 169–187. doi: 10.1016/j.matcom.2023.10.009 [20] G. Tang, S. Tang and R. A. Cheke, Global analysis of a Holling type Ⅱ predator–prey model with a constant prey refuge, Nonlinear Dynam., 2014, 76(1), 635–647. doi: 10.1007/s11071-013-1157-4 [21] S. Tang and L. Chen, The effect of seasonal harvesting on stage-structured population models, J. Math. Biol., 2004, 48(4), 357–374. doi: 10.1007/s00285-003-0243-5 [22] S. Tang, J. Liang, Y. Xiao and R. A. Cheke, Sliding bifurcations of Filippov two stage pest control models with economic thresholds, SIAM J. Appl. Math., 2012, 72(4), 1061–1080. doi: 10.1137/110847020 [23] J. Wang, S. He and L. Huang, Limit cycles induced by threshold nonlinearity in planar piecewise linear systems of node-focus or node-center type, Internat. J. Bifur. Chaos, 2020, 30(11), 2050160. doi: 10.1142/S0218127420501606 [24] J. Wang, C. Huang and L. Huang, Discontinuity-induced limit cycles in a general planar piecewise linear system of saddle–focus type, Nonlinear Anal. Hybrid Syst., 2019, 33, 162–178. doi: 10.1016/j.nahs.2019.03.004 [25] J. Wang and L. Huang, Limit cycles bifurcated from a focus-fold singularity in general piecewise smooth planar systems, J. Diff. Eqs., 2021, 304, 491–519. doi: 10.1016/j.jde.2021.10.006 [26] J. Wang, F. Zhang and L. Wang, Equilibrium, pseudoequilibrium and sliding-mode heteroclinic orbit in a Filippov-type plant disease model, Nonlinear Anal, Real World Appl., 2016, 31, 308–324. doi: 10.1016/j.nonrwa.2016.01.017 [27] D. Xiao, Dynamics and bifurcations on a class of population model with seasonal constant-yield harvesting, Discrete Contin. Dyn. Syst. Ser. B, 2016, 21(2), 699–719. [28] J. Yang, S. Tang and R. A. Cheke, Global stability and sliding bifurcations of a non-smooth Gause predator–prey system, Appl. Math. Comput., 2013, 224, 9–20. [29] J. Yu and J. Li, Global asymptotic stability in an interactive wild and sterile mosquito model, J. Diff. Eqs., 2020, 269(7), 6193–6215. doi: 10.1016/j.jde.2020.04.036 [30] J. Yu and J. Li, Adelay suppression model with sterile mosquitoes release period equal to wild larvae maturation period, J. Math. Biol., 2022, 84(3), 1–19. [31] Z. Zhang and B. Zheng, Dynamics of a mosquito population suppression model with a saturated Wolbachia release rate, Appl. Math. Lett., 2022, 129, 107933. doi: 10.1016/j.aml.2022.107933 [32] T. Zhao and Y. Xiao, Non-smooth plant disease models with economic thresholds, Math. Biosci., 2013, 241(1), 34–48. doi: 10.1016/j.mbs.2012.09.005 [33] B. Zheng, J. Yu and J. Li, Modeling and analysis of the implementation of the Wolbachia incompatible and sterile insect technique for mosquito population suppression, SIAM J. Appl. Math., 2021, 81(2), 718–740. doi: 10.1137/20M1368367 [34] Z. Zhu, X. Feng and L. Hu, Global dynamics of a mosquito population suppression model under a periodic release strategy, J. Appl. Anal. Comput., 2023, 13(4), 2297–2314. -
-
-
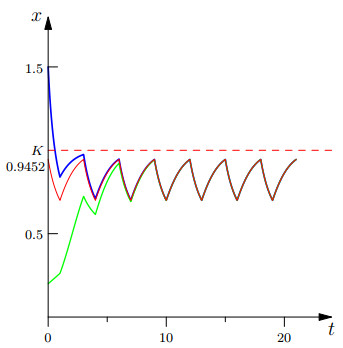
Figure 1.
Global asymptotical stability of the unique periodic solution with initial value
$ x(0)=0.9452 $ $ r=1, K=1, v=0.5, \bar{T}=1 $ $ T=3 $ -
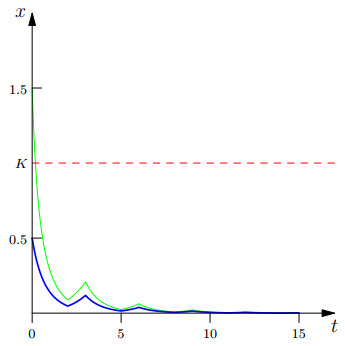
Figure 2.
Global asymptotical stability of
$ E_0=0 $ $ r=1, K=1, v=2, \bar{T}=2 $ $ T=3 $




 DownLoad:
DownLoad: