| Citation: |
Juan Zhang, Xiaonv Liang. FURTHER RESULTS OF M-EIGENVALUE LOCALIZATION THEOREM FOR FOURTH-ORDER PARTIALLY SYMMETRIC TENSORS AND THEIR APPLICATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3134-3161. doi: 10.11948/20230477
|
FURTHER RESULTS OF M-EIGENVALUE LOCALIZATION THEOREM FOR FOURTH-ORDER PARTIALLY SYMMETRIC TENSORS AND THEIR APPLICATIONS
-
Abstract
In this paper, we give some new M-eigenvalue inclusion theorems for fourth-order partially symmetric tensors, which are more tighter than some existing inclusion sets. On the basis, some new upper bounds of the M-spectral radius are presented. Further, as applications, we propose sufficient conditions for the strong ellipticity condition in the elastic materials. Numerical examples are shown to illustrate validity and superiority of our results.
-
-
References
[1] E. Azroul, A. Benkirane and M. Srati, Eigenvalue problem associated with nonhomogeneous integro-differential operators: Eigenvalue problem, Journal of Elliptic and Parabolic Equations, 2021, 7, 47–64. doi: 10.1007/s41808-020-00092-8 [2] H. Che, H. Chen and Y. Wang, On the m-eigenvalue estimation of fourth-order partially symmetric tensors, Journal of Industrial and Management Optimization, 2018, 16(1), 309–324. [3] H. Che, H. Chen and Y. Wang, M-positive semi-definiteness and m-positive definiteness of fourth-order partially symmetric cauchy tensors, Journal of Inequalities and Applications, 2019, 2019(1), 1–18. doi: 10.1186/s13660-019-1955-4 [4] S. Chiriţǎ, A. Danescu and M. Ciarletta, On the strong ellipticity of the anisotropic linearly elastic materials, Journal of Elasticity, 2007, 87(1), 1–27. doi: 10.1007/s10659-006-9096-7 [5] A. Cuyt, N. Flamand and F. Knaepkens, On the conditioning of some structured generalized eigenvalue problems, Maple Transactions, 2023, 3(3). [6] G. Dahl, J. M. Leinaas, J. Myrheim and E. Ovrum, A tensor product matrix approximation problem in quantum physics, Linear algebra and its applications, 2007, 420(2–3), 711–725. doi: 10.1016/j.laa.2006.08.026 [7] A. C. Doherty, P. A. Parrilo and F. M. Spedalieri, Distinguishing separable and entangled states, Physical Review Letters, 2002, 88(18), 187904. doi: 10.1103/PhysRevLett.88.187904 [8] M. Farcaseanu, A. Grecu, M. Mihailescu and D. Stancu-Dumitru, Perturbed eigenvalue problems: An overview, Studia Univ., Babes-Bolyai Math, 2021, 66, 55–73. doi: 10.24193/subbmath.2021.1.05 [9] L. Gurvits, Classical deterministic complexity of edmonds' problem and quantum entanglement, in Proceedings of the Thirty-Fifth Annual ACM Symposium on Theory of Computing, 2003, 10–19. [10] D. Han, H.-H. Dai and L. Qi, Conditions for strong ellipticity of anisotropic elastic materials, Journal of Elasticity, 2009, 97, 1–13. doi: 10.1007/s10659-009-9205-5 [11] J. He, C. Li and Y. Wei, M-eigenvalue intervals and checkable sufficient conditions for the strong ellipticity, Applied Mathematics Letters, 2020, 102, 106137. doi: 10.1016/j.aml.2019.106137 [12] J. He, Y. Liu and G. Xu, New s-type inclusion theorems for the m-eigenvalues of a 4th-order partially symmetric tensor with applications, Applied Mathematics and Computation, 2021, 398, 125992. doi: 10.1016/j.amc.2021.125992 [13] S. Herschenfeld and P. D. Hislop, Local eigenvalue statistics for higher-rank anderson models after dietlein-elgart, arXiv preprint arXiv: 2208.03598, 2022. [14] C. J. Hillar and L.-H. Lim, Most tensor problems are np-hard, Journal of the ACM (JACM), 2013, 60(6), 1–39. [15] Z.-H. Huang and L. Qi, Positive definiteness of paired symmetric tensors and elasticity tensors, Journal of Computational and Applied Mathematics, 2018, 338, 22–43. doi: 10.1016/j.cam.2018.01.025 [16] B. Jiang, Polynomial Optimization: Structures, Algorithms, and Engineering Applications, University of Minnesota, 2013. [17] J. K. Knowles and E. Sternberg, On the ellipticity of the equations of nonlinear elastostatics for a special material, Journal of Elasticity, 1975, 5(3–4), 341–361. doi: 10.1007/BF00126996 [18] S. Li, C. Li and Y. Li, M-eigenvalue inclusion intervals for a fourth-order partially symmetric tensor, Journal of Computational and Applied Mathematics, 2019, 356, 391–401. doi: 10.1016/j.cam.2019.01.013 [19] C. Ling, J. Nie, L. Qi and Y. Ye, Biquadratic optimization over unit spheres and semidefinite programming relaxations, SIAM Journal on Optimization, 2010, 20(3), 1286–1310. doi: 10.1137/080729104 [20] E. Mikhailov and M. Pashentseva, Eigenvalue problem for a reduced dynamo model in thick astrophysical discs, Mathematics, 2023, 11(14), 3106. doi: 10.3390/math11143106 [21] L. Qi, H. Chen and Y. Chen, Tensor Eigenvalues and their Applications, 39, Springer, 2018. [22] L. Qi, H.-H. Dai and D. Han, Conditions for strong ellipticity and m-eigenvalues, Frontiers of Mathematics in China, 2009, 4, 349–364. doi: 10.1007/s11464-009-0016-6 [23] L. Qi and Z. Luo, Tensor Analysis: Spectral Theory and Special Tensors, SIAM, 2017. [24] H. Simpson, S. Spector and E. Sternberg, On copositive matrices and strong ellipticity for isotropic elastic materials, Archive for Rational Mechanics and Analysis, 1983, 84(1), 55–68. doi: 10.1007/BF00251549 [25] G. Wang, L. Sun, L. Liu, et al., M-eigenvalues-based sufficient conditions for the positive definiteness of fourth-order partially symmetric tensors, Complexity, 2020, 2020. [26] Y. Wang and M. Aron, A reformulation of the strong ellipticity conditions for unconstrained hyperelastic media, Journal of Elasticity, 1996, 44, 89–96. doi: 10.1007/BF00042193 [27] Y. Wang, L. Qi and X. Zhang, A practical method for computing the largest m-eigenvalue of a fourth-order partially symmetric tensor, Numerical Linear Algebra with Applications, 2009, 16(7), 589–601. doi: 10.1002/nla.633 [28] S. Wright, J. Nocedal, et al., Numerical optimization, Springer Science, 1999, 35(67–68), 7. [29] H. Xiang, L. Qi and Y. Wei, On the m-eigenvalues of elasticity tensor and the strong ellipticity condition, arXiv preprint arXiv: 1708.04876, 2017. [30] H. Xiang, L. Qi and Y. Wei, M-eigenvalues of the riemann curvature tensor, arXiv preprint arXiv: 1802.10248, 2018. [31] L. Zee and E. Sternberg, Ordinary and strong ellipticity in the equilibrium theory of incompressible hyperelastic solids, Archive for Rational Mechanics and Analysis, 1983, 83(1), 53–90. doi: 10.1007/BF00281087 [32] X. Zhang, C. Ling and L. Qi, Semidefinite relaxation bounds for bi-quadratic optimization problems with quadratic constraints, Journal of Global Optimization, 2011, 49(2), 293–311. doi: 10.1007/s10898-010-9545-5 [33] X. Zhang, et al., Polynomial Optimization and its Applications, 2010. [34] Y. Zhang, L. Sun and G. Wang, Sharp bounds on the minimum M-eigenvalue of elasticity M-tensors, Mathematics, 2020, 8(2), 250. doi: 10.3390/math8020250 -
-
Figures(3) / Tables(2)
Export File
Citation
Juan Zhang, Xiaonv Liang. FURTHER RESULTS OF M-EIGENVALUE LOCALIZATION THEOREM FOR FOURTH-ORDER PARTIALLY SYMMETRIC TENSORS AND THEIR APPLICATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3134-3161. doi: 10.11948/20230477
Format
Content
DownLoad:
-
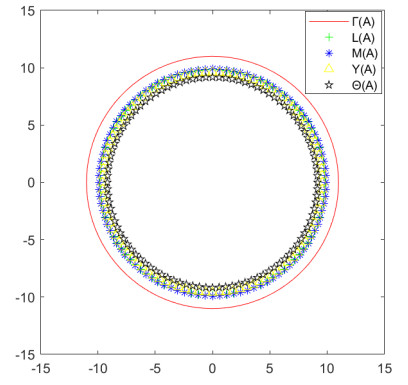
Figure 1.
Comparison of inclusion sets of Example 2.1.
-
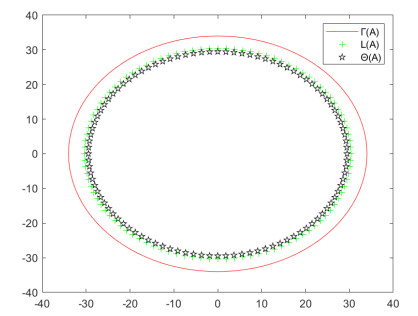
Figure 2.
Comparison of inclusion sets of Example 2.2.
-
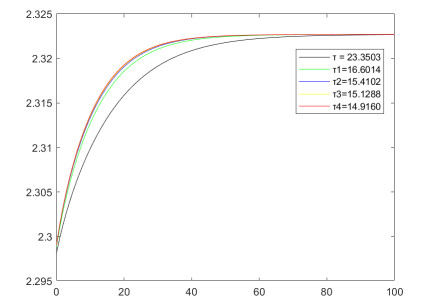
Figure 3.
Numerical results of Example 4.1.