| Citation: |
Shahid Abdullah, Neha Choubey, Suresh Dara. DYNAMICAL ANALYSIS OF OPTIMAL ITERATIVE METHODS FOR SOLVING NONLINEAR EQUATIONS WITH APPLICATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3349-3376. doi: 10.11948/20240009
|
DYNAMICAL ANALYSIS OF OPTIMAL ITERATIVE METHODS FOR SOLVING NONLINEAR EQUATIONS WITH APPLICATIONS
-
Abstract
In this study, we introduced a new family of two- and three-step iterative methods for solving non-linear equations. The proposed methods adhere to the Kung and Traub conjecture, making them optimal as they require only three function evaluations for a fourth-order method and four function evaluations for an eighth-order method per cycle. To achieve a fourth-order method, we employed linear combination technique merging Xiaojan's method with Yu and Xu's method, while for an eighth-order method, we utilized weight function approach. The convergence criteria of the proposed schemes are thoroughly covered in the two primary theorems. Through comparative analysis with existing methods using various nonlinear models and test functions, we conducted extensive numerical investigations to demonstrate the superior performance and efficacy of our proposed techniques. Furthermore, we explored the fractal behavior of our technique and other existing methods by considering different forms of complex functions within the basins of attraction.
-
-
References
[1] O. Y. Ababneh, New fourth order iterative methods second derivative free, Z. Angew. Math. Phys., 2016, 4(3), 519–523. [2] S. Abbasbandy, Improving Newton–Raphson method for nonlinear equations by modified Adomian decomposition method, Appl. Math. Comput., 2003, 145(2–3), 887–893. [3] S. Abdullah, N. Choubey and S. Dara, Optimal fourth-and eighth-order iterative methods for solving nonlinear equations with basins of attraction, Journal of Applied Mathematics and Computing, 2024. DOI: 10.1007/s12190-024-02108-1. [4] S. Abdullah, N. Choubey and S. Dara, An efficient two-point iterative method with memory for solving non-linear equations and its dynamics, Journal of Applied Mathematics and Computing, 2024, 70(1), 285–315. doi: 10.1007/s12190-023-01953-w [5] S. Abdullah, N. Choubey and S. Dara, Two Novel With and Without Memory Multi-Point Iterative Methods for Solving Non-Linear Equations, Communications in mathematics and applications, 2024. DOI: 10.26713/cma.v15i1.2432. [6] F. I. Chicharro, A. Cordero, N. Garrido and J. R. Torregrosa, Wide stability in a new family of optimal fourth-order iterative methods, Computational and Mathematical Methods, 2019. DOI: 10.1155/2024/2849717. [7] N. Choubey and J. P. Jaiswal, An improved optimal eighth-order iterative scheme with its dynamical behaviour, Int. J. Computing Science and Mathematics, 2016, 7(4), 361–370. doi: 10.1504/IJCSM.2016.078685 [8] C. Chun, M. Y. Lee, B. Neta and J. Džunić, On optimal fourth-order iterative methods free from second derivative and their dynamics, Appl. Math. Comput., 2012, 218(11), 6427–6438. [9] J. Džunić, M. S. Petković and L. D. Petković, A family of optimal three-point methods for solving nonlinear equations using two parametric functions, Appl. Math. Comput., 2011, 217(19), 7612–7619. [10] J. H. He and X. H. Wu, Variational iteration method: New development and applications, Compt. Math. Appl., 2007, 54(7–8), 881–894. [11] D. Jain, Families of newton-like methods with fourth-order convergence, Int. J. Comput., 2013, 90(5), 1072–1082. [12] J. P. Jaiswal and N. Choubey, A new efficient optimal eighth-order iterative method for solving nonlinear equations, arXiv preprint, 2013. arXiv: 1304.4702, [13] M. U. D. Junjua, S. Akram, N. Yasmin and F. Zafar, A new jarratt-type fourthorder method for solving system of nonlinear equations and applications, J. Appl. Math., 2015. DOI: 10.1155/2015/805278. [14] J. Kou, Y. Li and X. Wang, A composite fourth-order iterative method for solving non-linear equations, Appl. Math. Comput., 2007, 184(2), 471–475. [15] H. Kung and J. F. Traub, Optimal order of one-point and multipoint iteration, J. ACM, 1974, 21(4), 643–651. doi: 10.1145/321850.321860 [16] A. K. Maheshwari, A fourth order iterative method for solving nonlinear equations, Appl. Math. Comput., 2009, 211(2), 383–391. [17] A. Nadeem, A. Faisal and J. H. He, New optimal fourth-order iterative method based on linear combination technique, Hacet. J. Math. Stat., 2021, 50(6), 1692–1708. doi: 10.15672/hujms.909721 [18] A. Naseem, M. Rehman, S. Qureshi and N. A. D. Ide, Graphical and numerical study of a newly developed root-finding algorithm and its engineering applications, IEEE Access, 2023, 11, 2375–2383. doi: 10.1109/ACCESS.2023.3234111 [19] M. A. Noor and M. Waseem, Some iterative methods for solving a system of nonlinear equations, Compt. Math. Appl., 2009, 57(1), 101–106. doi: 10.1016/j.camwa.2008.10.067 [20] S. Panday, A. Sharma and G. Thangkhenpau, Optimal fourth and eighth-order iterative methods for non-linear equations, J. Appl. Math. Comput., 2023, 69(1), 953–971. doi: 10.1007/s12190-022-01775-2 [21] S. Qureshi, I. K. Argyros, A. Soomro, K. Gdawiec, A. A. Shaikh and E. Hincal, A new optimal root-finding iterative algorithm: local and semilocal analysis with polynomiography, Numer. Algor., 2023. DOI: 10.1007/s11075-023-01625-7. [22] S. Qureshi, H. Ramos and A. Soomro, A new nonlinear ninth-order root-finding method with error analysis and basins of attraction, Mathematics, 2021. DOI: 10.1155/2022/7656451. [23] S. Qureshi, A. Soomro, A. A. Shaikh, E. Hincal and N. Gokbulut, A Novel Multistep Iterative Technique for Models in Medical Sciences with Complex Dynamics, Computational and Mathematical Methods in Medicine, 2022. DOI: 10.3390/math9161996. [24] M. Rafiullah, A fifth-order iterative method for solving nonlinear equations, Numer. Analys. Appl., 2011, 4(3), 297–302. [25] J. R. Sharma and H. Arora, An efficient family of weighted-newton methods with optimal eighth order convergence, Appl. Math. Lett., 2014 29, 1–6. [26] A. Singh and J. P. Jaiswal, An efficient family of optimal eighth-order iterative methods for solving nonlinear equations and its dynamics, J. Math., 2014. DOI: 10.1155/2014/569719. [27] R. Singh and S. Panday, Efficient optimal eighth order method for solving nonlinear equations, AIP Conference Proceedings, 2023. DOI: 10.1063/5.0144304. [28] O. S. Solaiman and I. Hashim, Efficacy of optimal methods for nonlinear equations with chemical engineering applications, Math. Probl. Eng., 2019. DOI: 10.1155/2019/1728965. [29] O. Solaiman and A. IshakHashim, The Attraction Basins of Several Root Finding Methods, With a Note About Optimal Methods, Proc. International Arab Conference on Mathematics and Computations, 2019. [30] H. Tari, D. D. Ganji and H. Babazadeh, The application of He's variational iteration method to nonlinear equations arising in heat transfer, Phys. Lett. A, 2007, 363(3), 213–217. doi: 10.1016/j.physleta.2006.11.005 [31] R. Thukral and M. Petković, A family of three-point methods of optimal order for solving nonlinear equations, J. Comput. Appl. Math., 2010, 233(9), 2278–2284. doi: 10.1016/j.cam.2009.10.012 [32] X. Yu and X. Xu, A new family of chebyshev-halley like methods free from second derivative, Fixed Pory Appl., 2012, 13(1), 319–325. [33] F. Zafar and N. A. Mir, A generalized family of quadrature based iterative methods, Gen. Math., 2010, 18(4), 43–51. [34] X. Zhou, Modified chebyshev–halley methods free from second derivative, Appl. Math. Comput., 2008, 203(2), 824–827. -
-
Figures(10) / Tables(10)
Export File
Citation
Shahid Abdullah, Neha Choubey, Suresh Dara. DYNAMICAL ANALYSIS OF OPTIMAL ITERATIVE METHODS FOR SOLVING NONLINEAR EQUATIONS WITH APPLICATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3349-3376. doi: 10.11948/20240009
Format
Content
DownLoad:
-
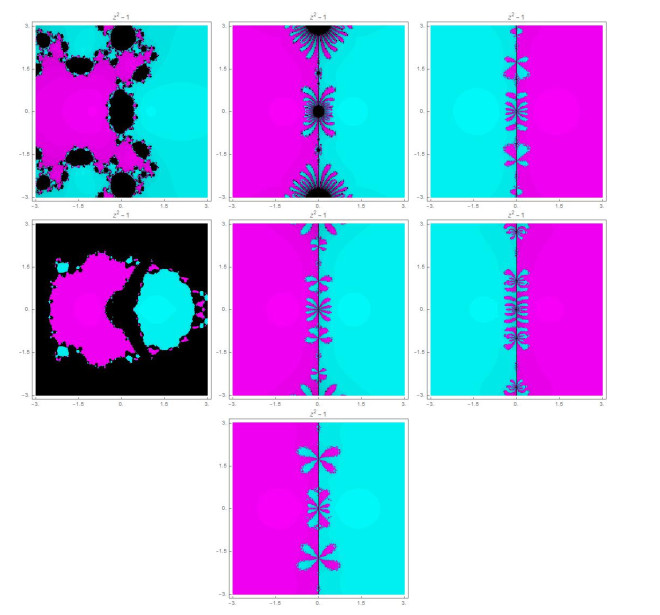
Figure 1.
Basins of attraction for
$ CC4 $ $ CH4 $ $ JJ4 $ $ AN4 $ $ MH4 $ $ SQ4 $ $ SA4 $ $ p_1(z) $ -
Figure 2.
Basins of attraction for
$ CC4 $ $ CH4 $ $ JJ4 $ $ AN4 $ $ MH4 $ $ SQ4 $ $ SA4 $ $ p_2(z) $ -
Figure 3.
Basins of attraction for
$ CC4 $ $ CH4 $ $ JJ4 $ $ AN4 $ $ MH4 $ $ SQ4 $ $ SA4 $ $ p_3(z) $ -
Figure 4.
Basins of attraction for
$ JH8 $ $ JM8 $ $ SP8 $ $ SJ8 $ $ MH8 $ $ RS8 $ $ SA8 $ $ p_1(z) $ -
Figure 5.
Basins of attraction for
$ JH8 $ $ JM8 $ $ SP8 $ $ SJ8 $ $ MH8 $ $ RS8 $ $ SA8 $ $ p_2(z) $ -
Figure 6.
Basins of attraction for
$ JH8 $ $ JM8 $ $ SP8 $ $ SJ8 $ $ MH8 $ $ RS8 $ $ SA8 $ $ p_3(z) $ -
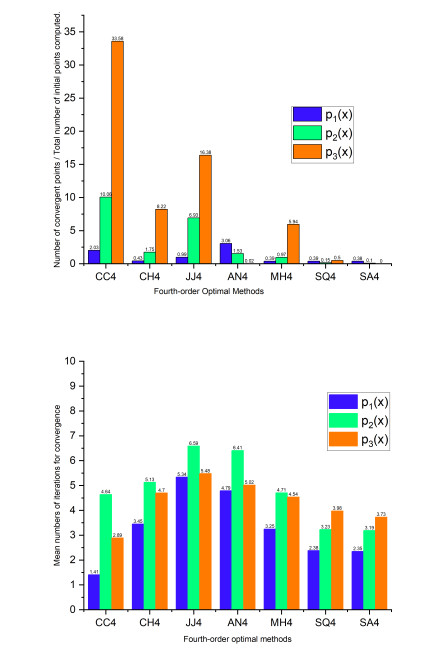
Figure 7.
Graphical comparisons of basins of attraction for
$ CC4 $ $ CH4 $ $ JJ4 $ $ AN4 $ $ SQ4 $ $ SA4 $ -
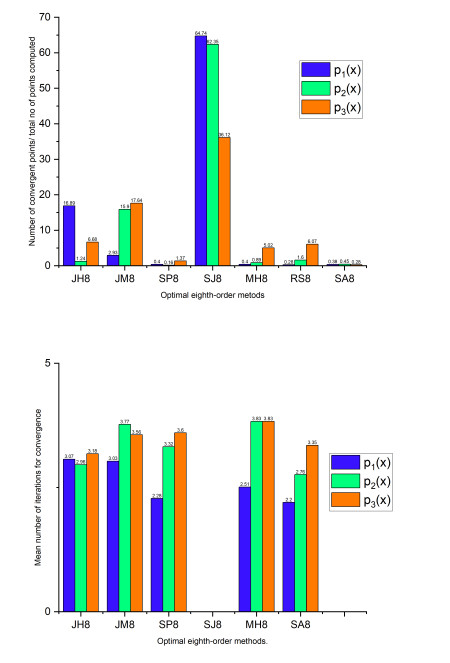
Figure 8.
Graphical comparisons of basins of attraction for
$ JH8 $ $ JM8 $ $ SP8 $ $ SJ8 $ $ MH8 $ $ RS8 $ $ SA8 $ -
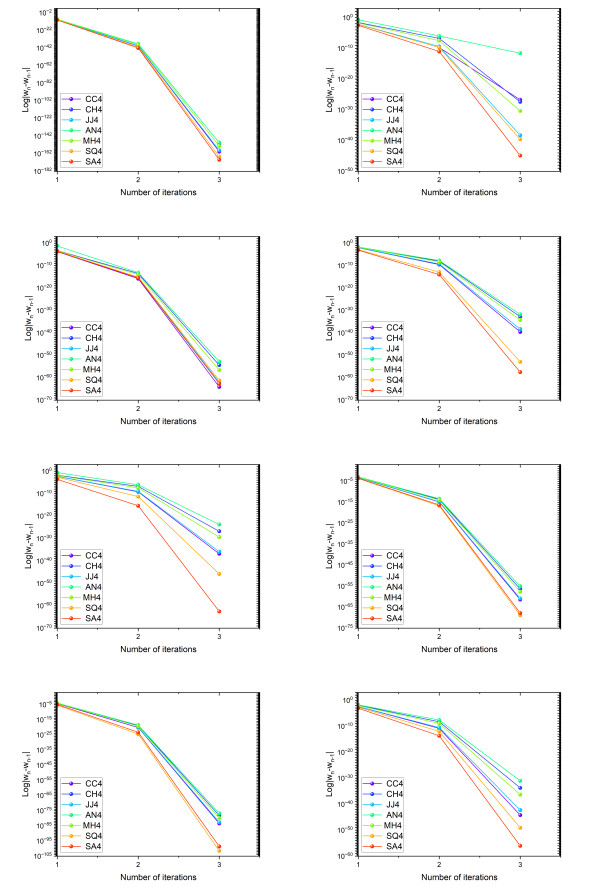
Figure 9.
Comparison of fourth-order methods based on the error in consecutive iterations,
$ |w_n- w_{n-1}| $ $ g_1(w) $ $ g_8(w) $ -
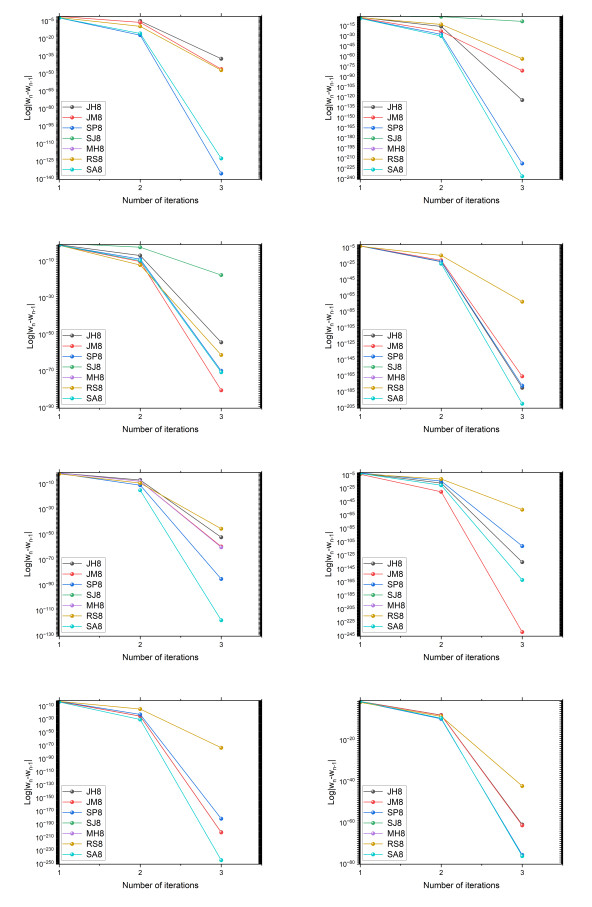
Figure 10.
Comparison of eighth-order methods based on the error in consecutive iterations,
$ |w_n- w_{n-1}| $ $ g_1(w) $ $ g_8(w) $