| Citation: | Meixiang Chen. BIFURCATIONS AND EXACT SOLUTIONS FOR THE KUNDU EQUATION: DYNAMICAL APPROACH[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3377-3384. doi: 10.11948/20240012 |
BIFURCATIONS AND EXACT SOLUTIONS FOR THE KUNDU EQUATION: DYNAMICAL APPROACH
-
Abstract
In this paper, we focus on the exact traveling wave solutions for the Kundu equation. By using the method of dynamical systems, we obtain bifurcations of the phase portraits of the corresponding planar dynamical system under different parameter conditions. Corresponding to different level curves, we derive all possible exact explicit parametric representations of the bounded solutions (including smooth periodic wave solutions, solitary solutions, kink wave solutions).
-
Keywords:
- Solitary wave /
- periodic wave /
- kink wave /
- bifurcation /
- dynamical system /
- Kundu equation
-

-
References
[1] P. F. Byrd and M. D. Friedman, Handbook of Elliptic Integrals for Engineers and Scientist, Springer, Berlin, 1971. [2] A. Choudhuri and K. Porsezian, Dark-in-the-Bright solitary wave solution of higher-order nonlinear Schrödinger equation with non-Kerr terms, Optics Communications, 2012, 285(3), 364–367. doi: 10.1016/j.optcom.2011.09.043 [3] N. A. Kudryashov, Implicit solitary waves for one of the generalized nonlinear Schrödinger equations, Mathematics, 2021, 9(23), 3024. doi: 10.3390/math9233024 [4] A. Kundu, Landau-Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schrödinger-type equations, J. Math. Phys., 1984, 25(12), 3433–3438. doi: 10.1063/1.526113 [5] J. Li, Singular Nonlinear Traveling Wave Equations: Bifurcations and Exact Solutions, Science Press, Beijing, 2013. [6] D. Qiu, J. He, Y. Zhang and K. Porsezian, The Darboux transformation of the Kundu-Eckhaus equation, Proc. R. Soc. A, 2015, 471, 20150236. doi: 10.1098/rspa.2015.0236 [7] D. Qiu and Y. Zhang, The explicit bound-state soliton of Kundu equation derived by Riemann–Hilbert problem, Applied Mathematics Letters, 2023, 135, 108443. doi: 10.1016/j.aml.2022.108443 [8] Y. Xiang, X. Dai, S. Wen, J. Guo and D. Fan, Controllable Raman soliton self-frequency shift in nonlinear metamaterials, Phys. Rev. A, 2011, 84, 033815. doi: 10.1103/PhysRevA.84.033815 [9] E. M. E. Zayed, R. M. A. Shohib, M. E. M. Alngar, et al., Solitons in magneto-optic waveguides with dual-power law nonlinearity, Phys. Lett. A, 2020, 384, 126697. doi: 10.1016/j.physleta.2020.126697 [10] Y. Zhang, J. Rao, Y. Cheng and J. He, Riemann-Hilbert method for the Wadati-Konno-Ichikawa equation: N simple poles and one higher-order pole, Physica D, 2019, 399, 173–185. doi: 10.1016/j.physd.2019.05.008 [11] Y. Zhang, X. Tao and S. Xu, The bound-state soliton solutions of the complex modified KdV equation, Inverse Problems, 2020, 36, 065003. doi: 10.1088/1361-6420/ab6d59 [12] Z. Zhang and E. Fan, Inverse scattering transform and multiple high-order pole solutions for the Gerdjikov-Ivanov equation under the zero/nonzero background, Z. Angew. Math. Phys., 2020, 71, 149. doi: 10.1007/s00033-020-01371-z -
-
-
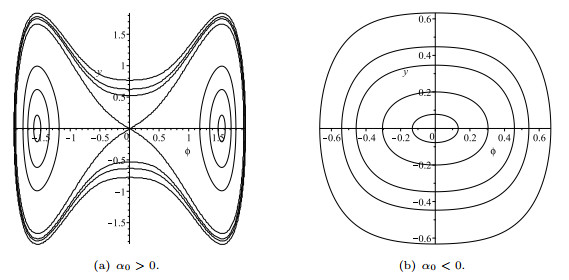
Figure 1.
The bifurcations of phase portraits of system (1.5) when
$ \alpha_0<0, \alpha_2>0, \Delta>0. $ -
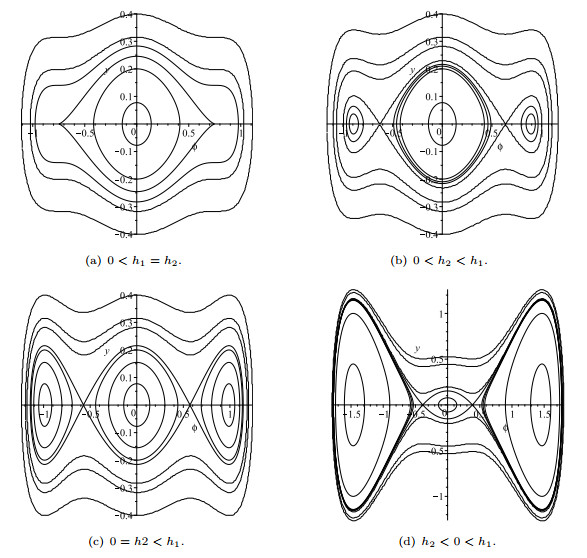
Figure 2.
Phase portraits of system (1.5) when
$ F(\psi) $




 DownLoad:
DownLoad: