| Citation: | Afaf Ahmima, Salim A. Messaoudi, Mohamed Alahyane. ON THE EXISTENCE AND STABILITY OF SOLUTIONS OF A TYPE-III THERMOELASTIC TRUNCATED TIMOSHENKO SYSTEM[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3385-3403. doi: 10.11948/20240019 |
ON THE EXISTENCE AND STABILITY OF SOLUTIONS OF A TYPE-III THERMOELASTIC TRUNCATED TIMOSHENKO SYSTEM
-
Abstract
This paper is concerned with the well-posedness and stability of a one-dimensional thermoelastic truncated Timoshenko system of Type III. In order to establish the well-posedness, we first solve an auxiliary problem and give the proof in details, using the semigroup theory and some non traditional operators. Then, we use this result to solve our original problem. After that, we prove that the presence of the thermal effect in one equation only is strong enough to drive the system exponentially to rest, irrespective to any relation between the coefficients. By the end of the work, we present some numerical tests to illustrate our theoretical findings.
-
Keywords:
- Exponential decay /
- Timoshenko /
- thermoelasticity type III /
- well-posedness /
- truncated
-

-
References
[1] M. Akil, Y. Chitour, M. Ghader and A. Wehbe, Stability and exact controllability of a Timoshenko system with only one fractional damping on the boundary, Asymptotic Analysis, 2020, 119(3–4), 221–280. doi: 10.3233/ASY-191574 [2] A. M. Al-Mahdi, M. M. Al-Gharabli, A. Guesmia and S. A. Messaoudi, New decay results for a viscoelastic-type Timoshenko system with infinite memory, Z. Angew. Math. Phys., 2020, 72(22), 1–43. [3] T. A. Apalara, S. A. Messaoudi and A. A. Keddi, On the decay rates of Timoshenko system with second sound, Math. Methods Appl. Sci., 2016, 39(10), 2671–2684. doi: 10.1002/mma.3720 [4] T. A. Apalara, C. A. Raposo and A. Ige, Thermoelastic Timoshenko system free of second spectrum, Appl. Math. Lett., 2022, 126, 107793. doi: 10.1016/j.aml.2021.107793 [5] M. A. Ayadi, A. Bchatnia, M. Hamouda and S. Messaoudi, General decay in a Timoshenko-type system with thermoelasticity with second sound, Adva. Nonlinear Anal., 2015, 4(4), 263–284. doi: 10.1515/anona-2015-0038 [6] A. Djebabla and N. E. Tatar, Exponential stabilization of the Timoshenko system by a thermo-viscoelastic damping, J. Dyn. Control Syst., 2010, 16(2), 189–210. doi: 10.1007/s10883-010-9089-5 [7] I. Elishakoff, An equation both more consistent and simpler than the Bresse-Timoshenko equation, SMIA. Adva. Math. Mode. Expe. Methods Mater. Stru., 2009, 168, 249–254. [8] I. Elishakoff, Who developed the so-called Timoshenko beam theory?, Math. Mech. Solids., 2020, 25(1), 97–116. doi: 10.1177/1081286519856931 [9] I. Elishakoff, F. Hache and N. Challamel, Variational derivation of governing differential equations for truncated version of Bresse-Timoshenko beams, J. Sound Vib., 2018, 435, 409–430. doi: 10.1016/j.jsv.2017.07.039 [10] B. Feng, On a semilinear Timoshenko-Coleman-Gurtin system: Quasi-stability and attractors, Discrete Contin. Dyn. Syst. Ser. A., 2017, 37(9), 4729–4751. doi: 10.3934/dcds.2017203 [11] B. Feng, D. S. Almeida, M. J. Dos Santos and L. G. Rosario Miranda, A new scenario for stability of nonlinear bresse-Timoshenko type systems with time dependent delay, ZAMM J. Appl. Math. Mech, Z. Angew. Math. Mech., 2020, 100(2), e201900160. doi: 10.1002/zamm.201900160 [12] B. Feng and X. G. Yang, Long-time dynamics for a nonlinear Timoshenko system with delay, Applicable Anal., 2017, 96(4), 606–625. doi: 10.1080/00036811.2016.1148139 [13] K. Ghennam and A. Djebabla, Energy decay result in a Timoshenko-type system of thermoelasticity of type III with weak damping, Math. Method. Appl. Sci., 2018, 41(10), 3868–3884. doi: 10.1002/mma.4873 [14] A. Guesmia and S. A. Messaoudi, On the control of a viscoelastic damped Timoshenko-type system, Appl. Math. Compt., 2008, 206(2), 589–597. doi: 10.1016/j.amc.2008.05.122 [15] A. Guesmia, S. A. Messaoudi and A. Soufyane, Stabilization of a linear Timoshenko system with infinite history and applications to the Timoshenko-heat systems, Electron. J. Differ. Equ., 2012, 193, 1–45. [16] D. S. A. Jùnior, A. J. A. Ramos and M. M. Freitas, Energy decay for damped Shear beam model and new facts related to the classical Timoshenko system, Appl. Math. Lett., 2021, 120, 107324. doi: 10.1016/j.aml.2021.107324 [17] D. S. A. Jùnior, A. J. A. Ramos, A. Soufyane, M. Cardoso and M. L. Santos, Issues related to the second spectrum, Ostrogradsky's energy and the stabilization of Timoshenko-Ehrenfest-type systems, Acta Mechanica., 2020, 231, 3565–3581. doi: 10.1007/s00707-020-02730-7 [18] D. S. A. Jùnior, A. J. A. Ramos, M. L. Santos and L. G. RM, Asymptotic behavior of weakly dissipative Bresse-Timoshenko system on influence of the second spectrum of frequency, ZAMM J. Appl. Math. Mech, Z. Angew. Math. Mech., 2018, 98(8), 1320–1333. doi: 10.1002/zamm.201700211 [19] D. S. A. Jùnior, M. L. Santos and J. E. Muñoz Rivera, Stability to weakly dissipative Timoshenko systems, Math. Methods Appl. Sci., 2013, 36(14), 1965–1976. doi: 10.1002/mma.2741 [20] D. S. A. Jùnior, M. L. Santos and J. E. M. Rivera, Stability to 1-d thermoelastic Timoshenko beam acting on shear force, Z. Angew. Math. Phys., 2014, 65(6), 1233–1249. doi: 10.1007/s00033-013-0387-0 [21] M. Kafini, S. A. Messaoudi and M. I. Mustafa, Energy decay result in a Timoshenko-type system of thermoelasticity of type III with distributive delay, J. Math. Phys., 2013, 54(10), 1–14. [22] A. Keddi, S. A. Messaoudi and M. Alahyane, On a thermoelastic Timoshenko system without the second spectrum: Existence and stability, J. Therm. Stre., 2023, 46(8), 823–838. doi: 10.1080/01495739.2023.2191662 [23] A. Malacarne and J. E. M. Rivera, Lack of exponential stability to Timoshenko system with viscoelastic Kelvin-Voigt type, Z. Angew. Math. Phys., 2016, 67(3), 1–10. [24] S. A. Messaoudi and A. Fareh, Energy decay in a Timoshenko-type system of ther- moelasticity of type III with different wave-propagation speeds, Arab. J. Math., 2013, 2(2), 199–207. doi: 10.1007/s40065-012-0061-y [25] S. A. Messaoudi and J. H. Hassan, General and optimal decay in a memory-type Timoshenko system, J. Integ Equ. Appl., 2018, 30(1), 117–145. [26] S. A. Messaoudi and M. I. Mustafa, A stability result in a memory-type Timoshenko system, Dyn. syst. appl., 2009, 18(3), 457. [27] S. A. Messaoudi and B. Said-Houari, Energy decay in a Timoshenko-type system of thermoelasticity of type III, J. Math. Anal. Appl., 2008, 348(1), 298–307. doi: 10.1016/j.jmaa.2008.07.036 [28] A. J. A. Ramos, D. S. A. Jùnior, M. M. Freitas and M. J. Dos Santos, A new exponential decay result for one-dimensional porous dissipation elasticity from second spectrum viewpoint, Appl. Math. Lett., 2020, 101, 106061. doi: 10.1016/j.aml.2019.106061 [29] A. J. A. Ramos, D. S. A. Jùnior and L. G. R. Miranda, An inverse inequality for a Bresse- Timoshenko system without second spectrum of frequency, Archiv der Mathematik., 2020, 114, 709–719. doi: 10.1007/s00013-020-01452-5 [30] X. Tian and Q. Zhang, Stability of a Timoshenko system with local Kelvin-Voigt damping, Z. Angew. Math. Phys., 2017, 68(20), 1–15. -
-
-
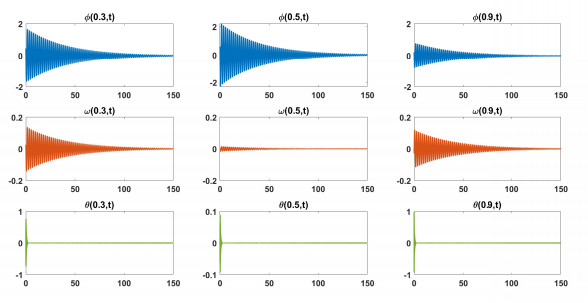
Figure 1.
Test 1: Damping cross section waves.
-
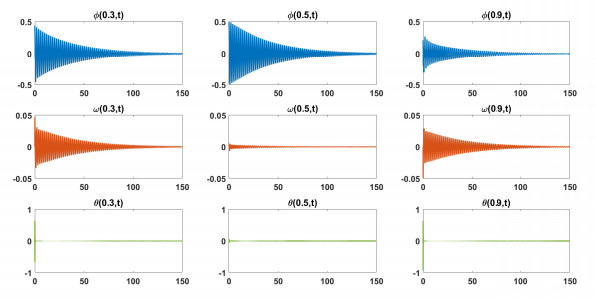
Figure 2.
Test 2: Damping cross section waves.
-
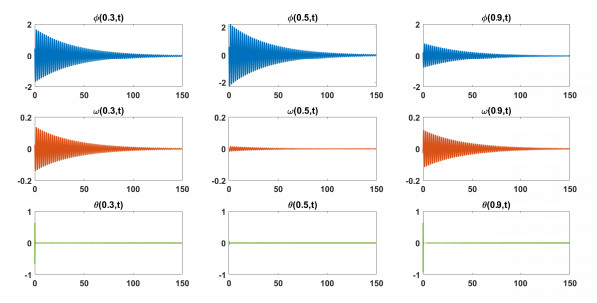
Figure 3.
Test 3: Damping cross section waves.
-
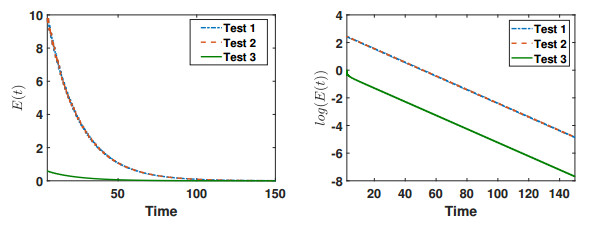
Figure 4.
Energy decay in natural and log scales.




 DownLoad:
DownLoad: