| Citation: |
Guodong Zhang, Huangyu Guo, Jing Han. HOPF BIFURCATION AND CONTROL FOR THE DELAYED PREDATOR-PREY MODEL WITH NONLINEAR PREY HARVESTING[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 2954-2976. doi: 10.11948/20240013
|
HOPF BIFURCATION AND CONTROL FOR THE DELAYED PREDATOR-PREY MODEL WITH NONLINEAR PREY HARVESTING
-
Abstract
In our study, we focused on investigating a delayed differential-algebraic system. The system incorporates a square root functional response and non-linear prey harvesting. Employing the normal form of differential algebraic systems and the central manifold theory, we conducted a detailed analysis of the system's stability and bifurcation phenomena, with time delay identified as a critical bifurcation parameter. When the time delay reached a critical value, the system's equilibrium points underwent the Hopf bifurcation, resulting in system instability. To achieve stability, we introduced a feedback controller, successfully transitioning the system from an unstable to a stable state. Through subsequent numerical simulations, we validated the accuracy and correctness of our research conclusions.
-
Keywords:
- Stability /
- predator-prey system /
- time delay /
- Hopf bifurcation /
- periodic solution
-
-
References
[1] B. Barman and B. Ghosh, Role of time delay and harvesting in some predator–prey communities with different functional responses and intra-species competition, International Journal of Modelling and Simulation, 2022, 42(6), 883–901. doi: 10.1080/02286203.2021.1983747 [2] B. Bhunia, L. T. Bhutia, T. K. Kar and P. Debnath, Explicit impacts of harvesting on a fractional-order delayed predator–prey model, The European Physical Journal Special Topics, 2023, 232(14), 2629–2644. [3] B. Bhunia, S. Ghorai, T. K. Kar, et al., A study of a spatiotemporal delayed predator–prey model with prey harvesting: Constant and periodic diffusion, Chaos, Solitons & Fractals, 2023, 175, 113967. [4] B. Bhunia, T. K. Kar and P. Debnath, Explicit impacts of harvesting on a delayed predator–prey system with allee effect, International Journal of Dynamics and Control, 2023, 1–15. [5] K. Chakraborty, M. Chakraborty and T. K. Kar, Bifurcation and control of a bioeconomic model of a prey–predator system with a time delay, Nonlinear Analysis: Hybrid Systems, 2011, 5(4), 613–625. doi: 10.1016/j.nahs.2011.05.004 [6] B. Chen, X. Liao and Y. Liu, Normal forms and bifurcations for the differential-algebraic systems, Acta Mathematicae Applicatae Sinica, 2000, 23(3), 429–443. doi: 10.3321/j.issn:0254-3079.2000.03.014 [7] W. Du, M. Xiao, J. Ding, et al., Fractional-order pd control at hopf bifurcation in a delayed predator–prey system with trans-species infectious diseases, Mathematics and Computers in Simulation, 2023, 205, 414–438. doi: 10.1016/j.matcom.2022.10.014 [8] T. Faria and L. T. Magalhães, Normal forms for retarded functional differential equations with parameters and applications to hopf bifurcation, Journal of Differential Equations, 1995, 122(2), 181–200. doi: 10.1006/jdeq.1995.1144 [9] B. Ghosh, B. Barman and M. Saha, Multiple dynamics in a delayed predator-prey model with asymmetric functional and numerical responses, Mathematical Methods in the Applied Sciences, 2023, 46(5), 5187–5207. doi: 10.1002/mma.8825 [10] H. S. Gordon, The economic theory of a common-property resource: The fishery, Journal of Political Economy, 1954, 62(2), 124–142. doi: 10.1086/257497 [11] H. Guo, J. Han and G. Zhang, Hopf bifurcation and control for the bioeconomic predator–prey model with square root functional response and nonlinear prey harvesting, Mathematics, 2023, 11(24), 4958. doi: 10.3390/math11244958 [12] B. D. Hassard, N. D. Kazarinoff and Y. -H. Wan, Theory and applications of Hopf bifurcation, 41, CUP Archive, 1981. [13] X. Jiao, X. Li and Y. Yang, Dynamics and bifurcations of a filippov leslie-gower predator-prey model with group defense and time delay, Chaos, Solitons & Fractals, 2022, 162, 112436. [14] F. Li and H. Li, Hopf bifurcation of a predator–prey model with time delay and stage structure for the prey, Mathematical and Computer Modelling, 2012, 55(3–4), 672–679. doi: 10.1016/j.mcm.2011.08.041 [15] Z. Liang and X. Meng, Stability and hopf bifurcation of a multiple delayed predator–prey system with fear effect, prey refuge and crowley–martin function, Chaos, Solitons & Fractals, 2023, 175, 113955. [16] W. Liu and Y. Jiang, Bifurcation of a delayed gause predator-prey model with michaelis-menten type harvesting, Journal of Theoretical Biology, 2018, 438, 116–132. doi: 10.1016/j.jtbi.2017.11.007 [17] J. Luo and Y. Zhao, Stability and bifurcation analysis in a predator–prey system with constant harvesting and prey group defense, International Journal of Bifurcation and Chaos, 2017, 27(11), 1750179. doi: 10.1142/S0218127417501796 [18] M. G. Mortuja, M. K. Chaube and S. Kumar, Dynamic analysis of a predator-prey system with nonlinear prey harvesting and square root functional response, Chaos, Solitons & Fractals, 2021, 148, 111071. [19] S. Ruan and J. Wei, On the zeros of transcendental functions with applications to stability of delay differential equations with two delays, Dynamics of Continuous Discrete and Impulsive Systems Series A, 2003, 10, 863–874. [20] N. Santra, S. Saha and G. Samanta, Role of multiple time delays on a stage-structured predator–prey system in a toxic environment, Mathematics and Computers in Simulation, 2023, 212, 548–583. [21] Q. Shi and Y. Song, Spatially nonhomogeneous periodic patterns in a delayed predator–prey model with predator-taxis diffusion, Applied Mathematics Letters, 2022, 131, 108062. [22] R. K. Upadhyay and R. Agrawal, Dynamics and responses of a predator–prey system with competitive interference and time delay, Nonlinear Dynamics, 2016, 83(1–2), 821–837. [23] Y. Wang and X. Zou, On a predator–prey system with digestion delay and anti-predation strategy, Journal of Nonlinear Science, 2020, 30(4), 1579–1605. [24] C. Xu, D. Mu, Y. Pan, et al., Exploring bifurcation in a fractional-order predator-prey system with mixed delays, J. Appl. Anal. Comput, 2023, 13, 1119–1136. [25] C. Xu, W. Zhang, C. Aouiti, et al., Bifurcation insight for a fractional-order stage-structured predator–prey system incorporating mixed time delays, Mathematical Methods in the Applied Sciences, 2023, 46(8), 9103–9118. [26] W. Yin, Z. Li, F. Chen and M. He, Modeling allee effect in the leslie-gower predator–prey system incorporating a prey refuge, International Journal of Bifurcation and Chaos, 2022, 32(6), 2250086. [27] G. Zhang, L. Zhu and B. Chen, Hopf bifurcation in a delayed differential–algebraic biological economic system, Nonlinear Analysis: Real World Applications, 2011, 12(3), 1708–1719. -
-
Figures(3)
Export File
Citation
Guodong Zhang, Huangyu Guo, Jing Han. HOPF BIFURCATION AND CONTROL FOR THE DELAYED PREDATOR-PREY MODEL WITH NONLINEAR PREY HARVESTING[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 2954-2976. doi: 10.11948/20240013
Format
Content
DownLoad:
-
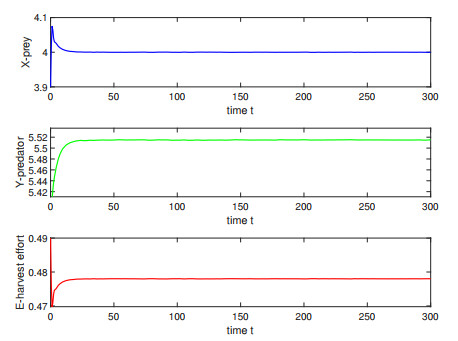
Figure 1.
Under the condition
$ \tau = 0.45 < \tau_{0} $ $ Y_{0} $ $ x_{0} = 3.9 $ $ y_{0} = 5.4 $ $ E_{0} = 0.49 $ -
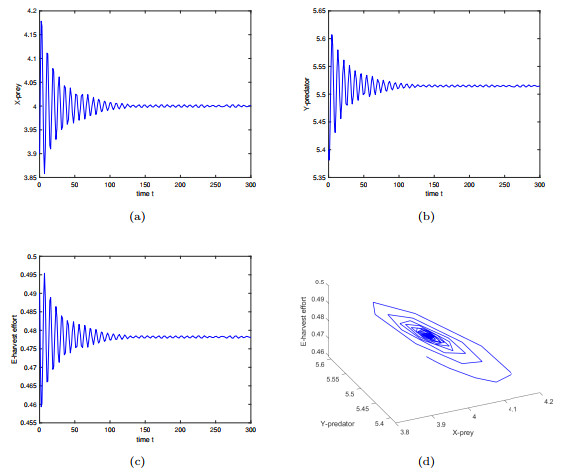
Figure 2.
At
$ \tau = 0.595 < \tau_{0} $ $ Y_{0} $ $ x_{0} = 3.9 $ $ y_{0} = 5.4 $ $ E_{0} = 0.49 $ -
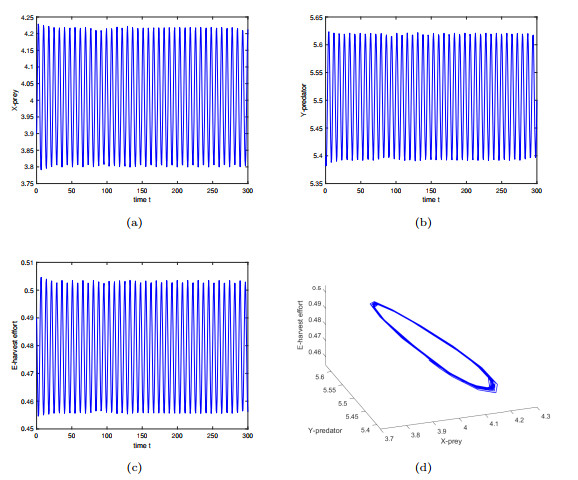
Figure 3.
When
$ k_{1}=1.3 > 0.98 $ $ Y_{0} $ $ x_{0} = 3.9 $ $ y_{0} = 5.4 $ $ E_{0} = 0.49 $