| Citation: | Ali Akgül, Nourhane Attia. ENHANCING SOLUTIONS FOR NON-LINEAR ORDINARY DIFFERENTIAL EQUATIONS VIA COMBINED LAPLACE TRANSFORM AND REPRODUCING KERNEL METHOD[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 226-244. doi: 10.11948/20240078 |
ENHANCING SOLUTIONS FOR NON-LINEAR ORDINARY DIFFERENTIAL EQUATIONS VIA COMBINED LAPLACE TRANSFORM AND REPRODUCING KERNEL METHOD
-
Abstract
Ordinary differential equations (ODEs) describe diverse phenomena in engineering and physics, such as electrical networks, oscillating systems, satellite orbits, and chemical reactions. Solving these equations, particularly the non-linear ones, is often challenging due to their complexity. This study aims to innovate by integrating the Laplace transform with the reproducing kernel Hilbert space method (RKHSM), introducing an enhanced approach that surpasses classical RKHSM. The combined Laplace-RKHSM method simplifies the original non-linear ODEs, allowing for the construction of novel numerical solutions. These solutions are systematically obtained in series form, providing both analytic and approximate results. The effectiveness and efficacy of the Laplace-RKHSM are demonstrated through three applications, each showcasing the method's superior performance in terms of accuracy and computational efficiency. This new approach not only enhances the existing RKHSM but also broadens its applicability to a wider range of non-linear problems in physics and engineering.
-

-
References
[1] O. Abu Arqub, J. Singh, B. Maayah and M. Alhodaly, Reproducing kernel approach for numerical solutions of fuzzy fractional initial value problems under the Mittag-Leffler kernel differential operator, Math. Meth. Appl. Sci., 2023, 46(7), 7965–7986. doi: 10.1002/mma.7305 [2] A. Akgül, A novel method for a fractional derivative with non-local and non-singular kernel, Chaos Solit. Fractals, 2018, 114, 478–482. doi: 10.1016/j.chaos.2018.07.032 [3] A. Akgül, A. Cordero and J. R. Torregrosa, Solutions of fractional gas dynamics equation by a new technique, Math. Meth. Appl. Sci., 2020, 43, 1349–1358. doi: 10.1002/mma.5950 [4] T. Allahviranloo and H. Sahihi, Reproducing kernel method to solve fractional delay differential equations, App. Math. Comput., 2021, 400, 126095. doi: 10.1016/j.amc.2021.126095 [5] F. M. Allehiany, M. H. DarAssi, I. Ahmad, M. A. Khan and E. M. Tag-Eldin, Mathematical Modeling and backward bifurcation in monkeypox disease under real observed data, Results Phys., 2023, 20, 106557. [6] A. M. Alqahtani, M. Ould Sidi, M. R. Khan, M. A. Elkotb, E. Tag-Eldin and A. M. Galal, Transport properties of two-dimensional dissipative flow of hybrid nanofluid with Joule heating and thermal radiation, Sci. Rep., 2022, 12(1), 19374. doi: 10.1038/s41598-022-23337-z [7] A. Atangana and A. Akgül, On solutions of fractal fractional differential equations, Discrete Contin. Dyn. Syst. Ser. A, 2021, 14(10), 3441–3457. [8] N. Attia, A. Akgül, D. Seba and A. Nour, An efficient numerical technique for a biological population model of fractional order, Chaos Solit. Fractals, 2020, 141, 110349. doi: 10.1016/j.chaos.2020.110349 [9] A. Attia, A. Akgül, D. Seba and A. Nour, On solutions of time-fractional advection-diffusion equation, Numer. Methods Partial Differ. Equ., 2023, 39(6), 4489–4516. doi: 10.1002/num.22621 [10] B. Azarnavid, The Bernoulli polynomials reproducing kernel method for nonlinear Volterra integro-differential equations of fractional order with convergence analysis, Comput. Appl. Math., 2022, 42(1), 8. [11] E. Babolian, S. Javadi and E. Moradi, RKM for solving Bratu-type differential equations of fractional order, Math. Meth. Appl. Sci., 2016, 39(6), 1548–1557. doi: 10.1002/mma.3588 [12] H. Beyrami and T. Lotfi, A novel method with error analysis for the numerical solution of a logarithmic singular Fredholm integral equation, Afr. Mat., 2023, 34(2), 33. doi: 10.1007/s13370-023-01073-5 [13] Y. Chellouf, B. Maayah, S. Momani, A. Alawneh and S. Alnabulsi, Numerical solution of fractional differential equations with temporal two-point BVPs using reproducing kernal Hilbert space method, AIMS Math., 2021, 6(4), 3465–3485. doi: 10.3934/math.2021207 [14] M. Cui and Y. Lin, Nonlinear Numerical Analysis in the Reproducing Kernel Space, Nova Science Publishers, Inc, New York, 2009. [15] F. Z. Geng, Numerical methods for solving Schrödinger equations in complex reproducing kernel Hilbert spaces, Math. Sci., 2020, 14(4), 293–299. doi: 10.1007/s40096-020-00337-6 [16] F. Geng and M. Cui, New method based on the HPM and RKHSM for solving forced Duffing equations with integral boundary conditions, J. Comput. Appl. Math., 2009, 233(2), 165–172. doi: 10.1016/j.cam.2009.07.007 [17] F. Geng and M. Cui, A reproducing kernel method for solving nonlocal fractional boundary value problems, Appl. Math. Lett., 2012, 25(5), 818–823. doi: 10.1016/j.aml.2011.10.025 [18] B. Ghanbari and A. Akgül, Abundant new analytical and approximate solutions to the generalized Schamel equation, Phys. Scr., 2020, 95(7), 075201. doi: 10.1088/1402-4896/ab8b27 [19] A. Ghasemi and A. Saadatmandi, A new Bernstein-reproducing kernel method for solving forced Duffing equations with integral boundary conditions, CMDE, 2024, 12(2), 329–337. [20] N. Harrouche, S. Momani, S. Hasan and M. Al-Smadi, Computational algorithm for solving drug pharmacokinetic model under uncertainty with nonsingular kernel type Caputo-Fabrizio fractional derivative, Alex. Eng. J., 2021, 60(5), 4347–4362. doi: 10.1016/j.aej.2021.03.016 [21] F. Hemati, M. Ghasemi and G. R. Khoshsiar, Numerical solution of the multiterm time-fractional diffusion equation based on reproducing kernel theory, Numer. Methods Partial Differ. Equ., 2021, 37(1), 44–68. doi: 10.1002/num.22518 [22] S. M. E. Ismaeel, Abdul-Majid Wazwaz, E. Tag-Eldin and S. A. El-Tantawy, Simulation studies on the dissipative modified Kawahara solitons in a complex plasma, Symmetry, 2023, 15(1), 57. [23] W. Jiang and T. Tian, Numerical solution of nonlinear Volterra integro-differential equations of fractional order by the reproducing kernel method, Appl. Math. Model., 2015, 39(16), 4871–4876. doi: 10.1016/j.apm.2015.03.053 [24] M. Modanli and A. Akgül, On solutions to the second-order partial differential equations by two accurate methods, Numer. Methods Partial Differ. Equ., 2018, 34(5), 1678–1692. doi: 10.1002/num.22223 [25] S. Momani, N. Djeddi, M. Al-Smadi and S. Al-Omari, Numerical investigation for Caputo-Fabrizio fractional Riccati and Bernoulli equations using iterative reproducing kernel method, Appl. Numer. Math., 2021, 170, 418–434. doi: 10.1016/j.apnum.2021.08.005 [26] M. G. Sakar, Iterative reproducing kernel Hilbert spaces method for Riccati differential equation, J. Comput. Appl. Math., 2017, 309, 163–174. doi: 10.1016/j.cam.2016.06.029 [27] M. G. Sakar, O. Saldır and A. Akgül, A novel technique for fractional Bagley-Torvik equation, Proc. Natl. Acad. Sci., India, Sect. A Phys. Sci., 2019, 89, 539–545. doi: 10.1007/s40010-018-0488-4 [28] S. A. A. Shah, N. A. Ahammad, B. Ali, K. Guedri, Aziz Ullah Awan, F. Gamaoun and E. M. Tag-ElDin, Significance of bio-convection, MHD, thermal radiation and activation energy across Prandtl nanofluid flow: A case of stretching cylinder, Int. Commun. Heat Mass Transf., 2022, 137, 106299. doi: 10.1016/j.icheatmasstransfer.2022.106299 [29] L. Shi, S. Tayebi, O. Abu Arqub, M. S. Osman, P. Agarwal, W. Mahamoud, M. Abdel-Aty and M. Alhodaly, The novel cubic B-spline method for fractional Painlevé and Bagley-Trovik equations in the Caputo, Caputo-Fabrizio, and conformable fractional sense, Alex. Eng. J., 2023, 65, 413–426. doi: 10.1016/j.aej.2022.09.039 [30] A. Tassaddiq, S. Qureshi, A. Soomro, O. Abu Arqub and M. Senol, Comparative analysis of classical and Caputo models for COVID-19 spread: Vaccination and stability assessment, Fixed Point Theory Algorithms Sci. Eng., 2024, 2024(2). [31] S. Zaremba, Sur le calcul numérique des fonctions demandées dans le problème de Dirichlet et le problème hydrodynamique, Bulletin International de l'Académie des Sciences de Cracovie, 1908, 68, 125–195. -
-
-
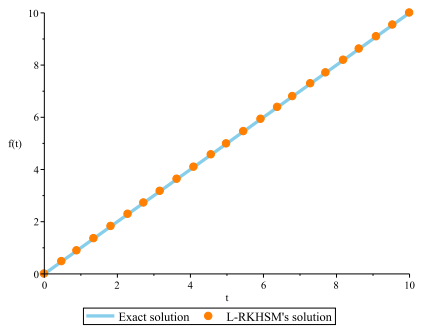
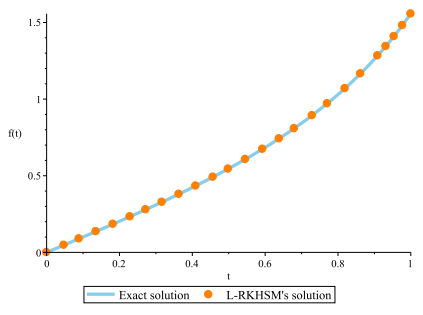
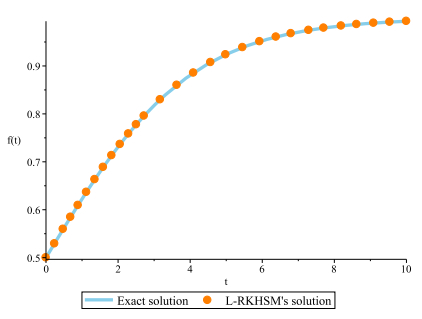
Figure 1.
Exact and L-RKHSM's solutions for Example 4.1.
-
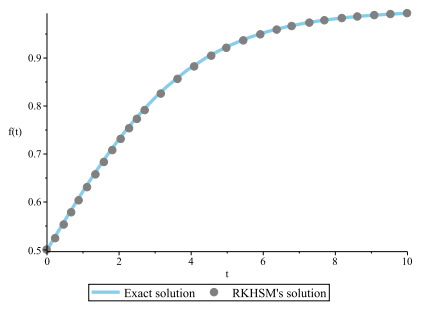
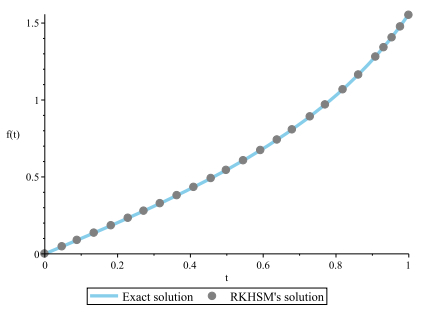
Figure 2.
Exact and RKHSM's solutions for Example 4.1.
-
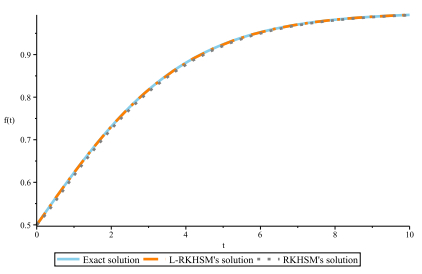
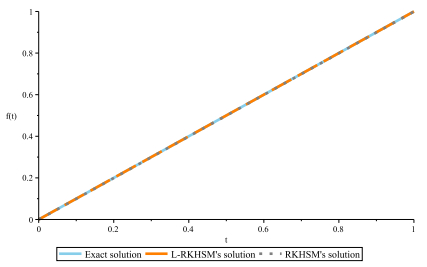
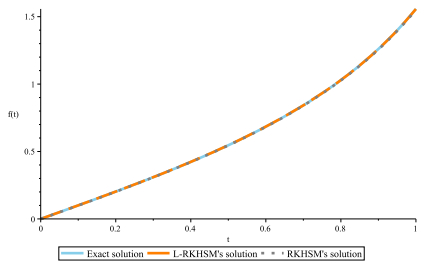
Figure 3.
Comparison between the three solutions: the Exact, L-RKHSM, and RKHSM solutions for Example 4.1.
-
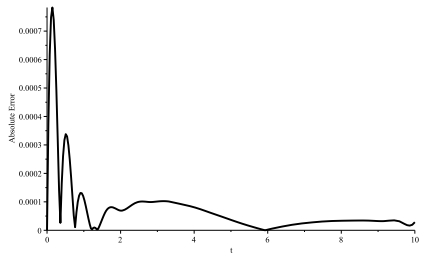
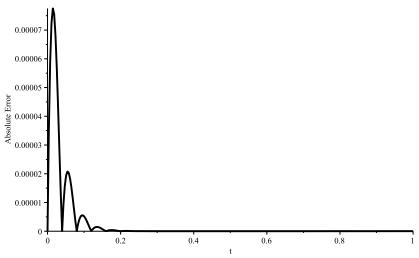
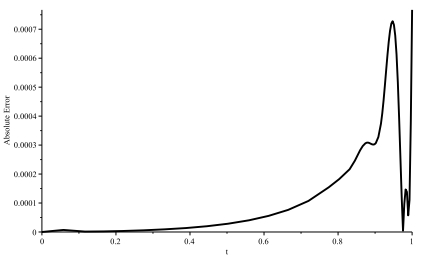
Figure 4.
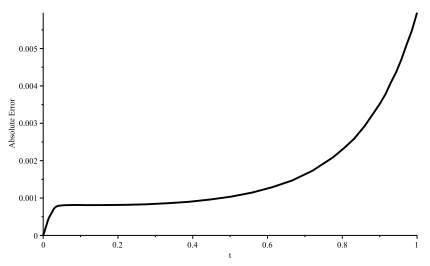
Absolute error of the L-RKHSM for Example 4.1.
-
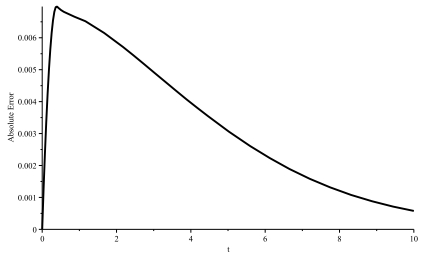
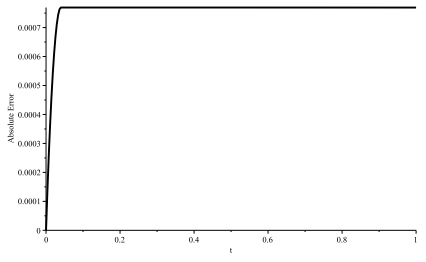
Figure 5.
Absolute error of the RKHSM for Example 4.1.
-
Figure 6.
Exact and L-RKHSM's solutions for Example 4.2.
-
Figure 7.
Exact and RKHSM's solutions for Example 4.2.
-
Figure 8.
Comparison between the three solutions: the Exact, L-RKHSM, and RKHSM solutions for Example 4.2.
-
Figure 9.
Absolute error of the L-RKHSM for Example 4.2.
-
Figure 10.
Absolute error of the RKHSM for Example 4.2.
-
Figure 11.
Exact and L-RKHSM's solutions for Example 4.3.
-
Figure 12.
Exact and RKHSM's solutions for Example 4.3.
-
Figure 13.
Comparison between the three solutions: the Exact, L-RKHSM, and RKHSM solutions for Example 4.3.
-
Figure 14.
Absolute error of the L-RKHSM for Example 4.3.
-
Figure 15.
Absolute error of the RKHSM for Example 4.3.




 DownLoad:
DownLoad: