| Citation: |
Fan Yang, Lu-Lu Yan, Hao Liu, Xiao-Xiao Li. TWO REGULARIZATION METHODS FOR IDENTIFYING THE UNKNOWN SOURCE OF SOBOLEV EQUATION WITH FRACTIONAL LAPLACIAN[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 198-225. doi: 10.11948/20240065
|
TWO REGULARIZATION METHODS FOR IDENTIFYING THE UNKNOWN SOURCE OF SOBOLEV EQUATION WITH FRACTIONAL LAPLACIAN
-
Abstract
In this paper, an inverse source problem for the Sobolev equation with fractional Laplacian is investigated. We prove that this kind of problem is ill-posed and apply the Quasi-boundary regularization method and fractional Landweber iterative regularization method to solve this inverse problem. Based on the result of conditional stability, the error estimates between the exact solution and the regularization solution are given under the priori and posteriori regularization parameter selection rules. Finally, three examples are given to illustrate the effectiveness and feasibility of these methods.
-
Keywords:
- Sobolev equation /
- inverse problem /
- identifying source term /
- regularization method
-
-
References
[1] H. M. Ahmed, M. M. El-Borai, H. M. El-Owaidy and A. S. Ghanem, Existence solution and controllability of Sobolev type delay nonlinear fractional integro-differential system, Mathematics, 2019, 7(1), 79. doi: 10.3390/math7010079 [2] J. Banasiak, N. A. Manakova and G. A. Sviridyuk, Positive solutions to Sobolev type equations with relatively p-sectorial operators, Bull. South Ural. State Univ. Ser. Math. Model. Program., 2020, 13(2), 17–32. [3] G. I. Barenblatt, Y. P. Zheltov and I. N. Kochina, Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks, J. Appl. Math., 1960, 24(5), 1286–1303. [4] M. K. Beshtokov, Numerical analysis of initial-boundary value problem for a Sobolev-type equation with a fractional-order time derivative, Comput. Math. Math. Phys., 2019, 59(2), 175–192. doi: 10.1134/S0965542519020052 [5] A. Favini, G. Sviridyuk and M. Sagadeeva, Linear Sobolev type equations with relatively p-radial operators in space of "noises", Mediterr. J. Math., 2016, 13(6), 4607–4621. doi: 10.1007/s00009-016-0765-x [6] K. M. Gamzaev, Inverse problem of unsteady incompressible fluid flow in a pipe with a permeable wall, Bull. South Ural State Univ. Ser. Math. Mech. Phys., 2020, 12(1), 24–30. [7] Y. Gao, D. Li, F. Yang and X. Li, Fractional Landweber iterative regularization method for solving the inverse problem of time-fractional Schrödinger equation, Symmetry, 2022, 14(10), 2010. doi: 10.3390/sym14102010 [8] M. O. Korpusov, A. A. Panin and A. E. Shishkov, On the critical exponent 'instantaneous blow-up' versus 'local solubility' in the Cauchy problem for a model equation of Sobolev type, Izv. Math., 2021, 85(1), 111–144. doi: 10.1070/IM8949 [9] Y. S. Li and T. Wei, An inverse time-dependent source problem for a time-space fractional diffusion equation, Appl. Math. Comput., 2018, 336, 257–271. [10] F. W. Liu, V. V. Anh, I. Turner and P. Zhuang, Time fractional advection-dispersion equation, J. Appl. Math. Comput., 2003, 13(1), 233–245. [11] D. Mehdi, S. Nasim and A. Mostafa, Application of spectral element method for solving Sobolev equations with error estimation, Appl. Numer. Math., 2020, 158, 439–462. doi: 10.1016/j.apnum.2020.08.010 [12] M. T. Mohan, On the three dimensional Kelvin-Voigt fluids: Global solvability, exponential stability and exact controllability of Galerkin approximations, Evol. Equ. Control The., 2020, 9(2), 301–339. doi: 10.3934/eect.2020007 [13] A. C. Natalí and S. Analía, Three solutions for a nonlocal problem with critical growth, J. Math. Anal. Appl., 2019, 469(2), 841–851. doi: 10.1016/j.jmaa.2018.09.038 [14] D. P. Nguyen, T. N. Van and L. LeDinh, Inverse source problem for Sobolev equation with fractional Laplacian, J. Funct. Space., 2022, 2022(1), 1–12. [15] D. E. Shafranov, On numerical solution in the space of differential forms for one stochastic Sobolev-type equation with a relatively radial operator, J. Comput. Eng. Math., 2020, 7(4), 48–55. doi: 10.14529/jcem200405 [16] D. E. Shafranov and N. V. Adukova, Solvability of the Showalter-Sidorov problem for Sobolev type equations with operators in the form of first-order polynomials from the Laplace-Beltrami operator on differential forms, J. Comput. Eng. Math., 2017, 4(3), 27–34. doi: 10.14529/jcem170304 [17] A. N. Tikhonov and V. Y. Arsenin, Solutions of ill-posed problems, Math. Comput., 1977, 32(144), 491–491. [18] M. Vauhkonen, D. Vadasz, P. A. Karjalainen, E. Somersalo and J. P. Kaipio, Tikhonov regularization and prior information in electrical impedance tomography, IEEE T. Med. Imaging, 1998, 17(2), 285–293. doi: 10.1109/42.700740 [19] J. Wang, On a nonlocal problem with critical Sobolev growth, Appl. Math. Lett., 2020, 99, 105959. doi: 10.1016/j.aml.2019.06.030 [20] T. Wei and Y. S. Li, Identifying a diffusion coefficient in a time-fractional diffusion equation, Math. Comput. Simulat., 2018, 151, 77–95. [21] X. T. Xiong, X. M. Xue and Z. Qian, A modified iterative regularization method for ill-posed problems, Appl. Numer. Math., 2017, 122(1), 108–128. [22] X. T. Xiong, L. Zhao and Y. C. Hon, Stability estimate and the modified regularization method for a Cauchy problem of the fractional diffusion equation, J. Comput. Appl. Math., 2014, 272, 180–194. [23] F. Yang, H. Wu and X. Li, Three regularization methods for identifying the initial value of homogeneous anomalous secondary diffusion equation, Math. Method. Appl. Sci., 2021, 44(17), 13723–13755. [24] F. Yang, H. Wu and X. Li, Three regularization methods for identifying the initial value of time fractional advection-dispersion equation, Comput. Appl. Math., 2022, 41(1), 1–38. [25] F. Yang, J. M. Xu and X. X. Li, Regularization methods for identifying the initial value of time fractional pseudo-parabolic equation, Calcolo, 2022, 59(4), 47. [26] A. A. Zamyshlyaeva and E. V. Bychkov, The Cauchy problem for the Sobolev type equation of higher order, Bull. South Ural State Univ. Ser. Math. Model. Program., 2018, 11(1), 5–14. [27] A. A. Zamyshlyaeva and A. V. Lut, Inverse problem for sobolev type mathematical models, Bull. South Ural State Univ. Ser. Math. Model. Program., 2019, 12(2), 25–36. [28] Z. Z. Zhang, W. H. Deng and H. T. Fan, Finite difference schemes for the tempered fractional Laplacian, Numer. Math. Theory Method. Appl., 2019, 12(2), 492–516. -
-
Figures(6)
Export File
Citation
Fan Yang, Lu-Lu Yan, Hao Liu, Xiao-Xiao Li. TWO REGULARIZATION METHODS FOR IDENTIFYING THE UNKNOWN SOURCE OF SOBOLEV EQUATION WITH FRACTIONAL LAPLACIAN[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 198-225. doi: 10.11948/20240065
Format
Content
DownLoad:
-
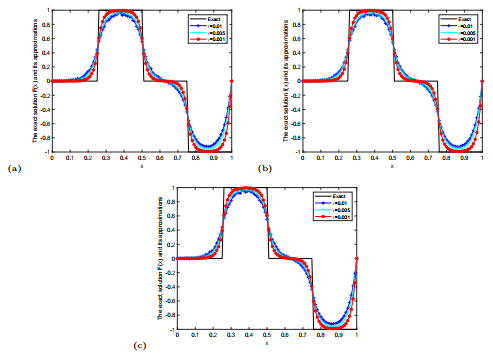
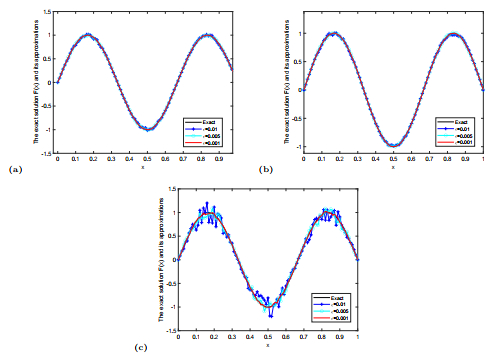
Figure 1.
The comparison of the exact solution
$ F(x) $ $ F^{m, \delta}(x) $ $ 5.1 $ $ \beta=1.1(a), 1.2(b), 1.3(c) $ $ \varepsilon=0.01, 0.005, 0.001. $ -
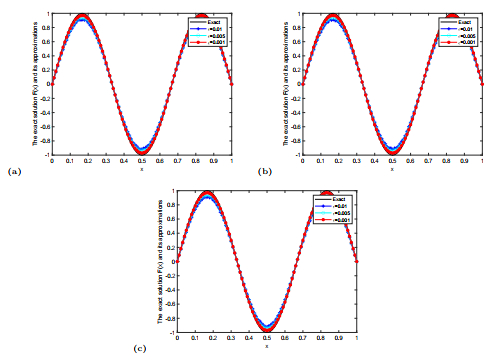
Figure 2.
The comparison of the exact solution
$ F(x) $ $ F^{m, \delta}(x) $ $ 5.2 $ $ \beta=1.1(a), 1.2(b), 1.3(c) $ $ \varepsilon=0.01, 0.005, 0.001. $ -
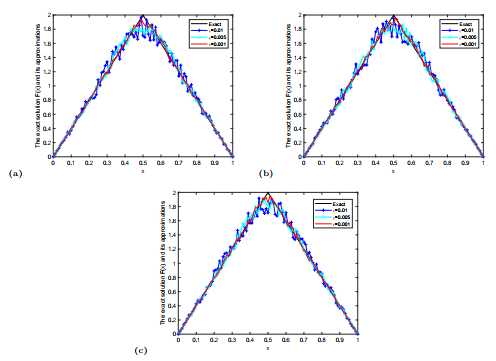
Figure 3.
The comparison of the exact solution
$ F(x) $ $ F^{m, \delta}(x) $ $ 5.3 $ $ \beta=1.1, 1.2, 1.3 $ $ \varepsilon=0.01, 0.005, 0.001. $ -
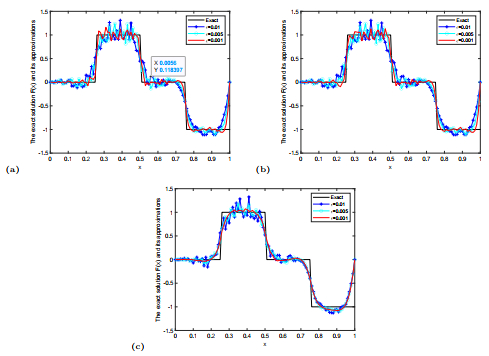
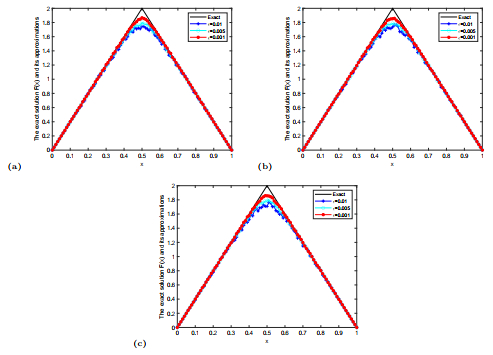
Figure 4.
The comparison of the exact solution
$ F(x) $ $ F^{m, \delta}(x) $ $ 5.1 $ $ \beta=1.1(a), 1.2(b), 1.3(c) $ $ \varepsilon=0.01, 0.005, 0.001. $ -
Figure 5.
The comparison of the exact solution
$ F(x) $ $ F^{m, \delta}(x) $ $ 5.2 $ $ \beta=1.1(a), 1.2(b), 1.3(c) $ $ \varepsilon=0.01, 0.005, 0.001. $ -
Figure 6.
The comparison of the exact solution
$ F(x) $ $ F^{m, \delta}(x) $ $ 5.3 $ $ \beta=1.1(a), 1.2(b), 1.3(c) $ $ \varepsilon=0.01, 0.005, 0.001. $