| Citation: |
Bin Liu, Jing Hu, Libo Liu. FINITE TIME STABILITY AND OPTIMAL CONTROL OF A STOCHASTIC REACTION DIFFUSION ECHINOCOCCOSIS MODEL WITH IMPULSE AND TIME-VARYING DELAY[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 160-197. doi: 10.11948/20240021
|
FINITE TIME STABILITY AND OPTIMAL CONTROL OF A STOCHASTIC REACTION DIFFUSION ECHINOCOCCOSIS MODEL WITH IMPULSE AND TIME-VARYING DELAY
-
Abstract
This paper presents a model for echinococcosis which incorporates stochastic reaction diffusion, impulse, and time-varying delay. First, the existence and uniqueness of global positive solution is proved through the construction of a Lyapunov function. Then, by applying the bounded impulse interval method, several sufficient conditions for finite time stability (FTS) are obtained. Finally, from the angle of cost-benefit, the issue of optimal control of echinococcosis is presented with the aim of minimizing infection and controlling costs. The validity of the analytical results is verified by numerical simulations.
-
Keywords:
- Finite-time stability /
- Lyapunov functional /
- optimal control /
- time-varying delay
-
-
References
[1] R. Azlaf, A. Dakkak, A. Chentou and M. Berrahmani, Modelling the transmission of echinococcus grataulosus in dogs in the northwest and in the southwest of Morocco, Vet. Parasitol., 2007, 145, 297-303. doi: 10.1016/j.vetpar.2006.12.014 [2] I. A. Baba, R. A. Abdulkadir and P. Esmaili, Analysis of tuberculosis model with saturated incidence rate and optimal control, Physica A, 2020, 123237, 540. [3] J. F. Banas and A. G. Vacroux, Optimal piecewise constant control of contitauous time systems with time-varying delay, Automatica, 1970, 6(6), 809-811. doi: 10.1016/0005-1098(70)90029-4 [4] P. A. Cabrera, G. Haran, U. Benavidez, S. Valledor, G. Perera, S. Lloyd, M. A. Gemmell, M. Baraibar, A. Morana, J. Maissonave and M. Carballo, Transmission dynamics of echinococcus grataulosus, taenia hydatigena and taenia ovis in sheep in Uruguay, Int. J. Parasitol., 1995, 25, 807-813. doi: 10.1016/0020-7519(94)00209-7 [5] J. Chai, Epidemiological studies on cystic echinococcosis in China-a review, Biomed. Environ. Sci., 1995, 8, 122-136. [6] K. Chu, Multiple Pulmonary Hydatid Disease in Left Lung: Report of a Case, in: A Collection of Abstracts of Papers Presented at the Second National Symposium on Hydatidosis, Urumqi, China, 1992. [7] M. A. Gemmell, J. R. Lawson and M. G. Roberts, Population dynamics in echinococcosis and cysticercosis: Evaluation of the biological parameters of taenia hydatigena and T. ovis and comparison with those of echinococcus grataulosus, Parasitology, 1987, 94, 161-180. doi: 10.1017/S0031182000053543 [8] A. Gray, D. Greenhalgh, L. Hu, X. Mao and J. Pan, A stochastic differential equation SIS epidemic model, Siam. J. Appl. Math., 2011, 71(3), 876-902. doi: 10.1137/10081856X [9] M. L. Greer, L. Pujomenjouet and G. F. Webb, A mathematical analysis of the dynamics of prion proliferation, J. Theor. Biol., 2006, 242(3), 598-606. doi: 10.1016/j.jtbi.2006.04.010 [10] D. J. Higham, An algorithmic introduction to taumerical simulation of stochastic differential equations, SIAM Rev., 2001, 43(3), 525-546. doi: 10.1137/S0036144500378302 [11] J. Hu, Q. Zhang, M. B. Anke and M. Ye, Finite-time stability and optimal control of a stochastic reaction-diffusion model for Alzheimer's disease with impulse and time-varying delay, Applied Mathematical Modelling., 2022, 102, 511-539. doi: 10.1016/j.apm.2021.10.004 [12] L. Huang, Y. Huang, Q. Wang, N. Xiao, D. Yi, W. Yu and D. Qiu, An agent-based model for control strategies of echinococcus grataulosus, Vet. Parasitol., 2011, 179(1-3), 84-91. doi: 10.1016/j.vetpar.2011.01.047 [13] S. Lahmar, H. Debbek, L. H. Zhang, D. P. McMataus, A. Souissi, S. Chelly and P. R. Torgerson, Transmission dynamics of the echinococcus grataulosus sheepšCdog strain(G1 genotype) in camels in Tunisia, Vet. Parasitol., 2004, 121, 151-156. doi: 10.1016/j.vetpar.2004.02.016 [14] S. Lenhart and J. T. Workman, Optimal Control Applied to Biological Models, John Chapman and Hall, 2007. [15] J. Liu, L. Liu, X. Fang and J. Fang, Global dynamics of a time-delayed echinococcosis transmission model, Adv. Differ. Equations, 2015, (2015), 1-16. [16] J. Lu, D. W. C. Ho and J. Cao, A unified synchronization criterion for impulsive dynamical networks, Automatica, 2010, 46(7), 1215-1221. doi: 10.1016/j.automatica.2010.04.005 [17] T. Pan, D. Jiang, H. Tasawar and A. Ahmed, Extinction and periodic solutions for an impulsive SIR model with incidence rate stochastically perturbed, Physica A, 2018, 505, 385-397. doi: 10.1016/j.physa.2018.03.012 [18] S. Portet and J. Arino, An in vivo intermediate filament assembly model, Mathematical Biosciences Engineering, 2008, 6(1), 117-134. [19] M. G. Roberts, J. R. Lawson and M. A. Gemmell, Population dynamics in echinococcosis and cysticercosis: Mathematical model of the life-cycles of taenia hydatigena and T. ovis. Parasitology, 1987, 94, 181-197. [20] P. R. Torgerson, I. Ziadinov, D. Aknazarov, R. Taurgaziev and P. Deplazes, Modelling the age variation of larval protoscoleces of echinococcus grataulosus in sheep, Int. J. Parasitol., 2009, 39, 1031-1035. doi: 10.1016/j.ijpara.2009.01.004 [21] E. Tornatore, S. M. Buccellato and P. Vetro, Stability of a stochastic SIR system, Physica. A, 2005, 354, 111-126. doi: 10.1016/j.physa.2005.02.057 [22] K. Wang, K. Zhang, Z. Jin, et al., Modeling and analysis of the transmission of echinococcosis with application to Xinjiang Uygur autonomous region of China, J. Theor. Biol., 2013, 333, 78-90. doi: 10.1016/j.jtbi.2013.04.020 [23] Z. Wang, X. Wang and X. Liu, Echinococcos is in China, a review of the epidemiology of echinococcus spp. EcoHealth, 2008, 5, 115-126. [24] K. Wu and B. Chen, Synchronization of partial differential systems via diffusion coupling, IEEE Trans. Circuits Syst. I Regul. Pap., 2012, 59(11), 2655-2668. doi: 10.1109/TCSI.2012.2190670 [25] K. Wu, M. Na, L. Wang, X. Ding and B. Wu, Finite-time stability of implusive reaction-diffusion systems with and without time delay, Applied Mathematucs and Computatuin., 2019, 363, 124591. doi: 10.1016/j.amc.2019.124591 [26] Z. Xu and C. Ai, A spatial echinococcosis transmission model with time delays: Stability and traveling waves, Int. J. Biomath., 2017, 10, 1-32. [27] Y. Zhang and Y. Xiao, Modeling and analyzing the effects of fixed-time intervention on transmission dynamics of echinococcosis in Qinghai province, Math. Meth. Appl. Sci., 2020, 2020, 1-21. [28] W. Zhu, Progress and Present Status of Hydatid Disease Control in China in the Recent Eight Decades, in: Hami Prefectural Institute of Scientific and Technological Information, Hami, China, 1985. -
-
Figures(6) / Tables(1)
Export File
Citation
Bin Liu, Jing Hu, Libo Liu. FINITE TIME STABILITY AND OPTIMAL CONTROL OF A STOCHASTIC REACTION DIFFUSION ECHINOCOCCOSIS MODEL WITH IMPULSE AND TIME-VARYING DELAY[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 160-197. doi: 10.11948/20240021
Format
Content
DownLoad:
-
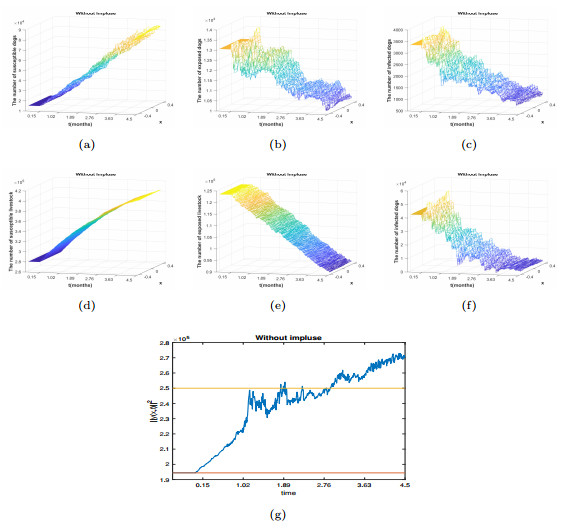
Figure 1.
The state trajectories of
$ y(x,t)=(S_1(x,t),E_1(x,t),I_1(x,t),S_2(x,t),E_2(x,t),I_2(x,t)) $ $ y(x,0)=(1.405\times10^4,1.3\times10^4,3.3\times10^3,2.78\times10^5,1.23\times10^5,4.16\times10^4) $ -
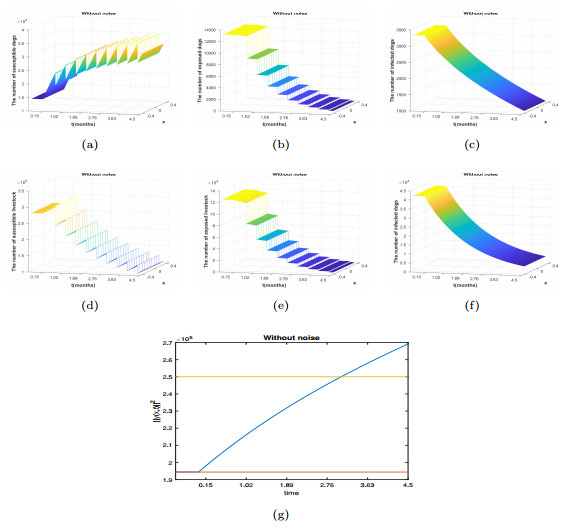
Figure 2.
The System (2.5) displays state trajectories for
$ y(t,x)=(S_1(t,x), E_1(t,x),I_1(t,x), S_2(t,x), E_2(t,x), I_2(t,x)) $ $ y(0,x)=(1.405\times10^4, 1.3\times10^4, 3.3\times10^3, 2.78\times10^5, 1.23\times10^5, 4.16\times10^4) $ -
Figure 3.
The System (2.5) displays state trajectories for
$ y(t,x)=(S_1(t,x), E_1(t,x), I_1(t,x), S_2(t,x), E_2(t,x), I_2(t,x)) $ $ y(0,x)=(1.405\times10^4, 1.3\times10^4, 3.3\times10^3, 2.78\times10^5, 1.23\times10^5, 4.16\times10^4) $ -
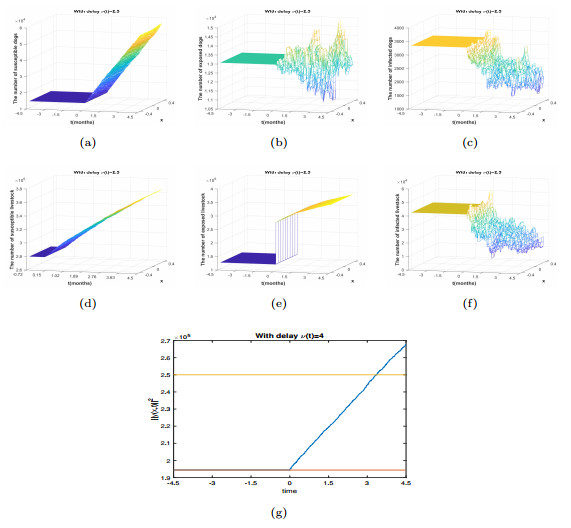
Figure 4.
The System (2.5) displays state trajectories for
$ y(t,x)=(S_1(t,x), E_1(t,x), I_1(t,x), S_2(t,x), E_2(t,x), I_2(t,x)) $ $ y(0,x)=(1.405\times10^4, 1.3\times10^4, 3.3\times10^3, 2.78\times10^5, 1.23\times10^5, 4.16\times10^4) $ $ \tau(t)=2.5 $ -
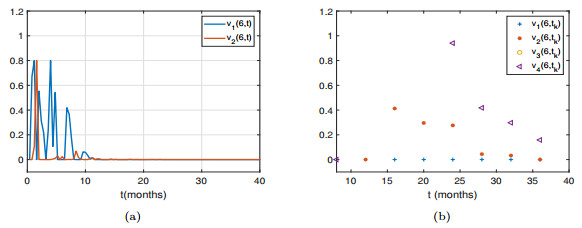
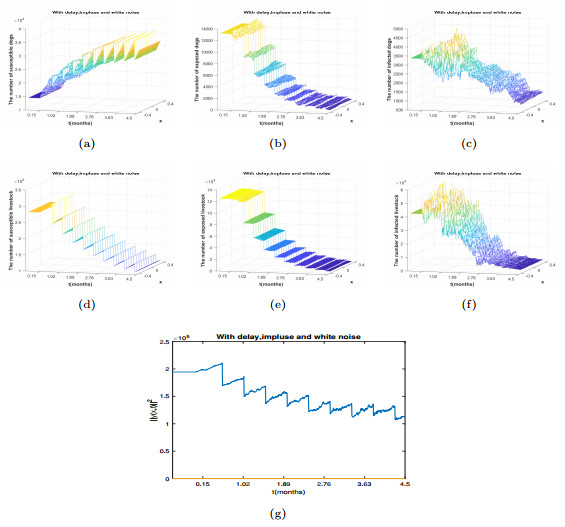
Figure 5.
The trajectories of
$ v_1(t,x),v_2(t,x) $ $ x=6 $ $ y(0,x)=(1.405\times10^4,1.3\times10^4,3.3\times10^3,2.78\times10^5,1.23\times10^5,4.16\times10^4) $ -
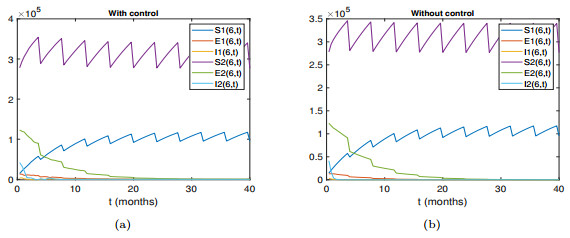
Figure 6.
The paths of
$ (S_1(t,x),E_1(t,x),I_1(t,x),S_2(t,x),E_2(t,x),I_2(t,x)) $ $ x=6 $ $ y(0,x)=(1.405\times10^4,1.3\times10^4,3.3\times10^3,2.78\times10^5,1.23\times10^5,4.16\times10^4) $