| Citation: | Longtao Chai, Lifei Wu, Xiaozhong Yang. A FAST PARALLEL DIFFERENCE METHOD FOR SOLVING THE TIME-FRACTIONAL GENERALIZED FISHER EQUATION[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1216-1240. doi: 10.11948/20240159 |
A FAST PARALLEL DIFFERENCE METHOD FOR SOLVING THE TIME-FRACTIONAL GENERALIZED FISHER EQUATION
-
Abstract
As a nonlinear fractional reaction-diffusion equation, the Time-Fractional Generalized Fisher (TFGF) equation is deeply rooted in physics, and its fast numerical methods' research has essential scientific significance and practical value. For the time-fractional generalized Fisher equation, based on the alternating segment technique, a parallel computation method for the Fast Alternating Segment Explicit-Implicit (FASE-Ⅰ) difference scheme is proposed. The time-fractional derivative is approximated by the fast L1 algorithm, while the spatial derivative is discretized by the alternating segment explicit-implicit difference method, the nonlinear term is processed using extrapolation. Theoretically analyze the FASE-Ⅰ method's uniqueness, stability, and convergence. Compared with the three classic difference methods, numerical experimental results show that the FASE-Ⅰ method not only has good computational accuracy; but also significantly improves computational efficiency. The FASE-Ⅰ method is efficient and feasible for resolving the time-fractional generalized Fisher equation.
-

-
References
[1] M. Adel, D. Baleanu, U. Sadiya, et al., Inelastic soliton wave solutions with different geometrical structures to fractional order nonlinear evolution equations, Results. Phys., 2022, 38. [2] W. Chen, H. Sun and X. Li, Fractional Derivative Modeling in Mechanics and Engineering, Springer, Singapore, 2022. [3] R. Choudhary, S. Singh and D. Kumar, A high-order numerical technique for generalized time-fractional Fisher's equation, Math. Method. Appl. Sci., 2023, 46(15, SI), 16050–16071. doi: 10.1002/mma.9435 [4] W. Deng and Z. Zhang, High Accuracy Algorithm for the Differential Equations Governing Anomalous Diffusion., World Scientific, Singapore, 2019. [5] E. G. M. Elmahdi and J. Huang, Efficient numerical solution of two-dimensional time-space fractional nonlinear diffusion-wave equations with initial singularity, J. Appl. Anal. Comput., 2022, 12(2), 831–849. [6] G. Gao, P. Xu and R. Tang, Fast compact difference scheme for the fourth-order time multi-term fractional sub-diffusion equations with the first Dirichlet boundary, J. Appl. Anal. Comput., 2021, 11(6), 2736–2761. [7] J. E. Gentle, Matrix Algebra: Theory, Computations and Applications in Statistics, Springer International Publishing, Cham, 2017. [8] A. Ghosh and C. Mishra, A parallel cyclic reduction algorithm for pentadiagonal systems with application to a convection-dominated heston PDE, SIAM. J. Sci. Comput., 2021, 43(2), C177–C202. doi: 10.1137/20M1311053 [9] B. Ghosh and J. Mohapatra, A novel numerical technique for solving time fractional nonlinear diffusion equations involving weak singularities, Math. Method. Appl. Sci., 2023, 46(12), 12811–12825. doi: 10.1002/mma.9214 [10] Z. He and R. Chen, A novel parallel parabolic equation method for electromagnetic scatterings, Ieee. T. Antenn. Propag., 2016, 64(11), 4777–4784. doi: 10.1109/TAP.2016.2600746 [11] Y. Huang, F. Zeng and L. Guo, Error estimate of the fast L1 method for time-fractional subdiffusion equations, Appl. Math. Lett., 2022, 133. [12] H. P. Jani and T. R. Singh, Aboodh Transform Homotopy Perturbation Method for Solving Fractional-Order Newell-Whitehead-Segel Equation, Math. Method. Appl. Sci., 2022. [13] S. Jiang, J. Zhang, Q. Zhang and Z. Zhang, Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations, Commun. Comput. Phys., 2017, 21(3), 650–678. [14] D. Kumar, S. Chaudhary and V. V. K. S. Kumar, Fractional Crank-Nicolson-Galerkin finite element scheme for the time-fractional nonlinear diffusion equation, Numer. Meth. Part. D. E., 2019, 35(6), 2056–2075. [15] D. Li, H. Liao, W. Sun, et al., Analysis of L1-Galerkin fems for time-fractional nonlinear parabolic problems, Commun. Comput. Phys., 2018, 24(1), 86–103. [16] D. Li, H. Qin and J. Zhang, Sharp pointwise-in-time error estimate of L1 scheme for nonlinear subdiffusion equations, J. Comput. Math., 2024, 42(3), 662–678. [17] F. Liu, P. Zhuang and Q. Liu, Numerical Methods of Fractional Partial Differential Equations and their Applications, Science Press, Beijing, 2015. (in Chinese). [18] N. Liu, Y. Liu, H. Li and J. Wang, Time second-order finite difference/finite element algorithm for nonlinear time-fractional diffusion problem with fourth-order derivative term, Comput. Math. Appl., 2018, 75(10), 3521–3536. [19] R. Liu and L. Wu, Numerical Approach for Solving Two-Dimensional Time-Fractional Fisher Equation via HABC-N Method, Commun. Appl. Math. Comput., 2023. [20] M. K. Riahi, Pitsbicg: Parallel in time stable bi-conjugate gradient algorithm, Appl. Numer. Math., 2022, 181, 225–233. [21] P. Roul and V. Rohil, A high order numerical technique and its analysis for nonlinear generalized Fisher's equation, J. Comput. Appl. Math., 2022, 406. [22] J. Shen, C. Li and Z. Sun, An H2N2 interpolation for Caputo derivative with order in (1, 2) and its application to time-fractional wave equations in more than one space dimension, J. Sci. Comput., 2020, 83(2). [23] Z. Sun and G. Gao, Fractional Differential Equations: Finite Difference Methods, De Gruyter, Berlin, Boston, 2020. [24] Z. Sun, Q. Zhang and G. Gao, Finite Difference Methods for Nonlinear Evolution Equations, De Gruyter, Berlin, Boston, 2023. [25] A. K. Y. Tam and M. J. Simpson, The effect of geometry on survival and extinction in a moving-boundary problem motivated by the Fisher-KPP equation, Physica. D., 2022, 438. [26] S. Trifce and T. Živorad, Fractional Equations and Models: Theory and Applications, Springer, Cham, 2019. [27] V. V. Uchaikin, Fractional Derivatives for Physicists and Engineers: Volume Ⅱ Applications, Higher Education Press, Beijing, 2013. [28] S. Vong, P. Lyu and Z. Wang, A compact difference scheme for fractional sub-diffusion equations with the spatially variable coefficient under Neumann boundary conditions, J. Sci. Comput., 2016, 66(2), 725–739. [29] F. Wang, M. N. Khan, I. Ahmad, et al., Numerical solution of traveling waves in chemical kinetics: Time-fractional Fishers equations, Fractals., 2022, 30(02). [30] K. Wang and J. Huang, A fast algorithm for the Caputo fractional derivative, E. Asian. J. Appl. Math., 2018, 8(4), 656–677. [31] W. Wang, H. Zhang, Z. Zhou and X. Yang, A fast compact finite difference scheme for the fourth-order diffusion-wave equation, Int. J. Comput. Math., 2024. [32] Y. Wang and Y. Zhang, A Crank-Nicolson-type compact difference method with the uniform time step for a class of weakly singular parabolic integro-differential equations, Appl. Numer. Math., 2022, 172, 566–590. [33] L. Wu and X. Yang, An efficient alternating segment parallel difference method for the time fractional telegraph equation, Adv. Math. Phys., 2020, 2020. [34] G. Xue and H. Feng, An alternating segment explicit-implicit scheme with intrinsic parallelism for Burgers' equation, J. Comput. Theor. Trans., 2020, 49(1), 15–30. [35] R. Yan, Y. He and Q. Zuo, A difference method with parallel nature for solving time-space fractional Black-Schole model, Chaos. Soliton. Fract., 2021, 151. [36] M. Yousuf, K. M. Furati and A. Q. M. Khaliq, A hybrid fourth order time stepping method for space distributed order nonlinear reaction-diffusion equations, Comput. Math. Appl., 2023, 151, 116–126. [37] Y. Yu, W. Deng and Y. Wu, Positivity and boundedness preserving schemes for the fractional reaction-diffusion equation, Sci. China Math., 2013, 56(10), 2161–2178. [38] W. Yuan, C. Zhang and D. Li, Linearized fast time-stepping schemes for time-space fractional Schrodinger equations, Physica. D., 2023, 454. [39] B. Zhu, L. Liu and Y. Wu, Existence and uniqueness of global mild solutions for a class of nonlinear fractional reaction-diffusion equations with delay, Comput. Math. Appl., 2019, 78(6), 1811–1818. -
-
-
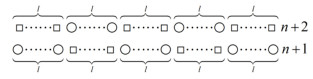
Figure 1.
The node segments in FASE-Ⅰ scheme.
-
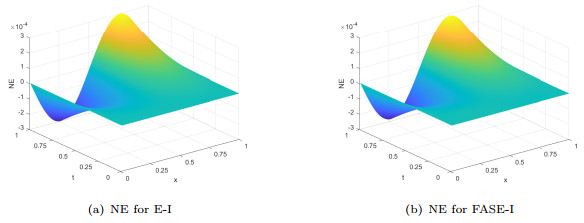
Figure 2.
NE distributions of the two methods for Example 4.1 (
$ \alpha=0.6 $ $ M=101 $ $ N=10000 $ -
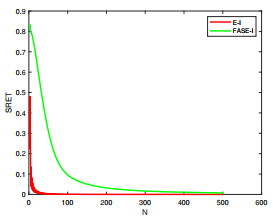
Figure 3.
Trend of the two methods' SRET for Example 4.1 (
$ \alpha=0.6 $ $ M=501 $ $ N=500 $ -
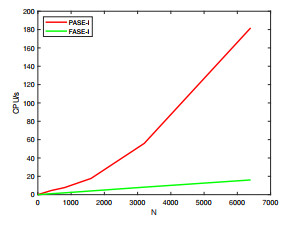
Figure 4.
CPU of the PASE-I and FASE-Ⅰ methods for Example 4.1 (
$ \alpha=0.6 $ $ M=1001 $ -
Figure 5.
CPU of the FE-I and FASE-Ⅰ methods for Example 4.1 (
$ \alpha=0.6 $ $ N=1000 $ -
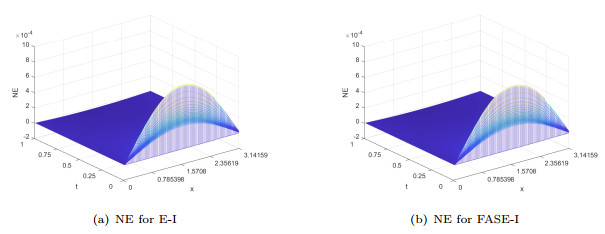
Figure 6.
NE distributions of the two methods for Example 4.2 (
$ \alpha=0.6 $ $ M=101 $ $ N=10000 $ -
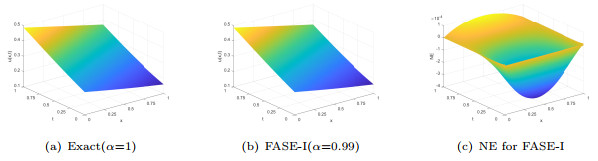
Figure 7.
Analytical solution surface, the FASE-Ⅰ method's numerical solution surface and node error distribution for Example 4.3 (
$ \alpha=0.99 $ $ M=501 $ $ N=1000 $ -
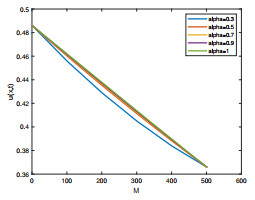
Figure 8.
The FASE-Ⅰ method solution curves (
$ \alpha=0.3,0.5,0.7,0.9 $ $ \alpha=1 $ $ M=501 $ $ N=1000 $




 DownLoad:
DownLoad: