| Citation: | Rui Zou, Hua Wei. A FINITE APPROXIMATE LIVŠIC THEOREM FOR ANOSOV DIFFEOMORPHISMS[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2185-2194. doi: 10.11948/20240420 |
A FINITE APPROXIMATE LIVŠIC THEOREM FOR ANOSOV DIFFEOMORPHISMS
-
Abstract
In this paper, we prove a finite approximate version of the Livšic theorem for Anosov diffeomorphisms. Let $f$ be a transitive Anosov diffeomorphism and $\varphi\in C^{\alpha}(M)$. We show that there exist $0<\beta\le \alpha, C>0$ and $\tau>0$ such that for any $\varepsilon>0$, if $\left|\sum_{i=0}^{n}\varphi\left(f^i(p)\right)\right|\le \varepsilon$ for each periodic point $ p=f^n(p)$ with $n\le \varepsilon^{-\frac{1}{2}}$, then there exist $u\in C^{\beta}(M)$ and $h\in C^{\beta}(M)$ such that $\varphi=u\circ f-u+h. $ Moreover, $\|u\|_{C^\beta}\le C$ and $\|h\|_{C^\beta}\le C\varepsilon^\tau.$
-
Keywords:
- Livšic theorem /
- Anosov diffeomorphisms /
- cohomological equations
-

-
References
[1] A. Avila, A. Kocsard and X. Liu, Livšic theorem for diffeomorphism cocycles, Geom. Funct. Anal., 2018, 28(4), 943–964. doi: 10.1007/s00039-018-0454-y [2] L. Backes, Rigidity of fiber bunched cocycles, Bull. Braz. Math. Soc. (N.S.), 2015, 46(2), 163–179. doi: 10.1007/s00574-015-0089-7 [3] L. Backes and A. Kocsard, Cohomology of dominated diffeomorphism-valued cocycles over hyperbolic systems, Ergodic Theory Dynam. Systems, 2016, 36(6), 1703–1722. doi: 10.1017/etds.2014.149 [4] S. Gan and D. Yu, Uniformly distributed periodic orbits of endomorphisms on torus. arXiv: 2407.19665. [5] S. Gouëzel and T. Lefeuvre, Classical and microlocal analysis of the x-ray transform on Anosov manifolds, Analysis & PDE, 2021, 14(1), 301–322. [6] C. E. Holanda and E. Santana, A Livšic-type theorem and some regularity properties for nonadditive sequences of potentials, J. Math. Phys., 2024, 65(8), Paper No. 082703. [7] W. Huang, Z. Lian and K. Lu, Ergodic theory of random anosov systems mixing on fibers. arXiv: 1612.08394. [8] B. Kalinin, Livšic theorem for matrix cocycles, Ann. of Math. (2), 2011, 173(2), 1025–1042. doi: 10.4007/annals.2011.173.2.11 [9] A. Katok and B. Hasselblatt, Introduction to the Modern Theory of Dynamical Systems, Encyclopedia Math. Appl., vol. 54, Cambridge Univ. Press, Cambridge, 1995. [10] S. Katok, Approximate solutions of cohomological equations associated with some anosov flows, Ergodic Theory Dynam. Systems, 1990, 10(2), 367–379. doi: 10.1017/S0143385700005605 [11] Z. Lian and J. Zhang, Livšic theorem for matrix cocycles over an Axiom A flow, Commun. Math. Stat., 2022, 10(4), 681–704. doi: 10.1007/s40304-021-00250-x [12] A. N. Livšic, Cohomology of dynamical systems, Izv. Akad. Nauk SSSR Ser. Mat., 1972, 36, 1296–1320. [13] A. N. Livšic, Homology properties of Y-systems, Math. Zametki, 1971, 10, 758–763. [14] R. de la Llave, J. M. Marco and R. Moriyón, Canonical perturbation theory of Anosov systems and regularity results for the Livšic cohomology equation, Ann. of Math. (2), 1986, 123(3), 537–611. doi: 10.2307/1971334 [15] R. de la Llave and M. Saprykina, Noncommutative coboundary equations over integrable systems, J. Mod. Dyn., 2023, 19, 773–794. doi: 10.3934/jmd.2023020 [16] V. Sadovskaya, Diffeomorphism cocycles over partially hyperbolic systems, Ergodic Theory Dynam. Systems, 2022, 42(1), 263–286. doi: 10.1017/etds.2020.131 [17] X. Su, P. Thieullen and W. Yu, Lipschitz sub-actions for locally maximal hyperbolic sets of a $ {C}^1$ maps, Discrete Contin. Dyn. Syst., 2024, 44(3), 656–677. doi: 10.3934/dcds.2023120 [18] X. Tian, Lyapunov 'non-typical' points of matrix cocycles and topological entropy. arXiv: 1505.04345. [19] A. Wilkinson, The cohomological equation for partially hyperbolic diffeomorphisms, Astérisque, 2013, (358), 75–165. [20] R. Zou and Y. Cao, Livšic theorem for banach cocycles: Existence and regularity, J. Funct. Anal., 2021, 280(5), 108889. doi: 10.1016/j.jfa.2020.108889 -
-
-
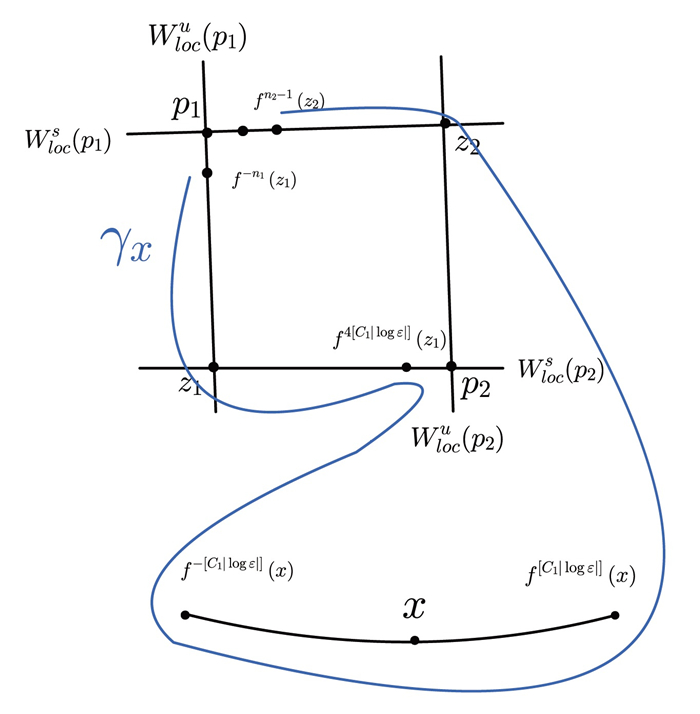
Figure 1.
Construction of
$ \gamma_x $




 DownLoad:
DownLoad: