| Citation: |
Yuxin Ma, Ruizhi Yang. BIFURCATION ANALYSIS IN A MODIFIED LESLIE-GOWER WITH NONLOCAL COMPETITION AND BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2152-2184. doi: 10.11948/20240415
|
BIFURCATION ANALYSIS IN A MODIFIED LESLIE-GOWER WITH NONLOCAL COMPETITION AND BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE
-
Abstract
In this paper, a diffusive predator-prey system with nonlocal competition and Beddington-DeAngelis functional response is considered. After analyzing the influence of the selected parameters on the existence, multiplicity and stability of the nonhomogeneous steady-state solution, it is obtained that there is an unstable positive nonconstant steady-state in the neighborhood of the positive constant steady-state. Compared with the system without nonlocal competition, the system with nonlocal competition can generate Hopf-Hopf bifurcation under certain conditions. Through the qualitative analysis, the normal form at the Hopf-Hopf bifurcation singularity is calculated to analyze the different dynamic properties exhibited by the system in different parameter regions. In order to illustrate the feasibility of the obtained results and the dependence of the dynamic behavior on the nonlocal competition, numerical simulations are carried out. Through the numerical simulations, it is further shown that under certain conditions, the nonlocal competition will lead to the generation of stable spatially inhomogeneous periodic solutions and stable spatially inhomogeneous quasi-periodic solutions.
-
-
References
[1] M. A. Aziz-Alaoui and M. D. Okiye, Boundedness and global stability for a predator-prey model with modified Leslie-Gower and Holling-type II schemes, Applied Mathematics Letters, 2003, 16(7), 1069–1075. doi: 10.1016/S0893-9659(03)90096-6 [2] Q. An and W. Jiang, Turing-Hopf bifurcation and Spatio-Temporal patterns of a ratio-dependent Holling-Tanner model with diffusion, International Journal of Bifurcation and Chaos, 2018, 28(9), 1850108. doi: 10.1142/S0218127418501080 [3] N. F. Britton, Aggregation and the competitive exclusion principle, Journal of Theoretical Biology, 1989, 136(1), 57–66. doi: 10.1016/S0022-5193(89)80189-4 [4] R. S. Cantrell and C. Cosner, On the dynamics of predator-prey models with the Beddington-DeAngelis functional response, Journal of Mathematical Analysis and Applications, 2001, 257(1), 206–222. doi: 10.1006/jmaa.2000.7343 [5] J. Cao, L. Ma and P. Hao, Bifurcation analysis in a modified Leslie-Gower predator-prey model with Beddington-Deangelis functional response, Journal of Applied Analysis and Computation, 2023, 13(5), 3026–3053. doi: 10.11948/20230183 [6] S. Chen and J. Yu, Stability and bifurcation on predator-prey systems with nonlocal prey competition, Discrete and Continuous Dynamical Systems, 2018, 38(1), 43–62. doi: 10.3934/dcds.2018002 [7] X. P. Chen, C. D. Huang, J. D. Cao, X. Y. Shi and A. Luo, Hopf bifurcation in the delayed fractional Leslie-Gower model with Holling-type II functional response, Journal of Applied Analysis and Computation, 2023, 13(5), 2555–2571. doi: 10.11948/20220451 [8] Y. F. Du, B. Niu, Y. X. Guo and J. J. Wei, Double Hopf bifurcation in delayed reaction-diffusion systems, Journal of Dynamics and Differential Equations, 2020, 32(1), 313–358. doi: 10.1007/s10884-018-9725-4 [9] M. Fan and Y. Kuang, Dynamics of a nonautonomous predator-prey system with the Beddington-DeAngelis functional response, Journal of Mathematical Analysis and Applications, 2004, 295(1), 15–39. doi: 10.1016/j.jmaa.2004.02.038 [10] J. Furter and M. Grinfeld, Local vs. non-local interactions in population dynamics, Journal of Mathematical Biology, 1989, 27(1), 65–80. doi: 10.1007/BF00276081 [11] J. P. Gao and S. J. Guo, Patterns in a modified Leslie-Gower model with Beddington-DeAngelis functional response and nonlocal prey competition, International Journal of Bifurcation and Chaos, 2020, 30(5), 2050074. doi: 10.1142/S0218127420500741 [12] M. Gazor, B. Hamzi and A. Shoghi, The infinite level normal forms for non-resonant double Hopf singularities, System and Control Letters, 2023, 176, 105529. doi: 10.1016/j.sysconle.2023.105529 [13] D. X. Geng, W. H. Jiang, Y. Lou and H. B. Wang, Spatiotemporal patterns in a diffusive predator-prey system with nonlocal intraspecific prey competition, Studies in Applied Mathematics, 2021, 148(1), 396–432. [14] D. Geng and H. Wang, Normal form formulations of double-Hopf bifurcation for partial functional differential equations with nonlocal effect, Journal of Differential Equations, 2021, 741–785. [15] J. Guckenheimer and P. Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer-Verlag, New York, 1983. [16] G. Guo and J. Wang, Pattern formation and qualitative analysis for a vegetation-water model with diffusion, Nonlinear Analysis: Real World Applications, 2024, 76, 104008. doi: 10.1016/j.nonrwa.2023.104008 [17] G. Guo, J. You and K. A. Abbakar, Pattern dynamics in a water-vegetation model with cross-diffusion and nonlocal delay, Mathematical Methods in the Applied Sciences, 2025, 48, 3190–3213. doi: 10.1002/mma.10480 [18] S. Guo, Global Hopf bifurcation of state-dependent delay differential equations, International Journal of Bifurcation and Chaos, 2023, 33(06), 2350074. doi: 10.1142/S0218127423500748 [19] J. Hale and S. V. Lunel, An Introduction to Functional-Differential Equations, Applied Mathematical Sciences, Springer-Verlag, New York, 1993. [20] T. W. Hwang, Global analysis of the predator-prey system with Beddington-DeAngelis functional response, Journal of Mathematical Analysis and Applications, 2003, 281(1), 395–401. doi: 10.1016/S0022-247X(02)00395-5 [21] G. R. Itovich and J. L. Moiola, Non-resonant double Hopf bifurcations: The complex case, Journal of Sound and Vibration, 2009, 322(1–2), 358–380. [22] X. Jia, K. Huang and C. Li, Bifurcation analysis of a modified Leslie-Gower predator-prey system, International Journal of Bifurcation and Chaos, 2023, 33(02), 2350024. doi: 10.1142/S0218127423500244 [23] W. Jiang, Q. An and J. Shi, Formulation of the normal form of Turing-Hopf bifurcation in partial functional differential equations, Journal of Differential Equations, 2020, 268(10), 6067–6102. doi: 10.1016/j.jde.2019.11.039 [24] T. T. Liu, L. J. Chen, F. D. Chen and Z. Li, Dynamics of a Leslie-Gower model with weak Allee effect on prey and fear effect on predator, International Journal of Bifurcation and Chaos, 2023, 33(01), 2350008. doi: 10.1142/S0218127423500086 [25] Y. Ma and R. Yang, Hopf-Hopf bifurcation in a predator-prey model with nonlocal competition and refuge in prey, Discrete and Continuous Dynamical Systems-Series B, 2023, 29(6), 2582–2609. [26] S. M. Merchant and W. Nagata, Instabilities and spatiotemporal patterns behind predator invasions with nonlocal prey competition, Theoretical Population Biology, 2011, 80(4), 289–297. doi: 10.1016/j.tpb.2011.10.001 [27] Y. Mi, C. Song and Z. Wang, Global boundedness and dynamics of a diffusive predator-prey model with modified Leslie-Gower functional response and density-dependent motion, Communications in Nonlinear Science and Numerical Simulation, 2023, 119, 107115. doi: 10.1016/j.cnsns.2023.107115 [28] A. F. Nindjin, M. A. Aziz-Alaoui and M. Cadivel, Analysis of a predator-prey model with modified Leslie-Gower and Holling-type II schemes with time delay, Nonlinear Analysis Real World Applications, 2006, 7(5), 1104–1118. doi: 10.1016/j.nonrwa.2005.10.003 [29] L. Pei, Q. Wang and H. Shi, Bifurcation dynamics of the modified physiological model ofartificial pancreas with insulin secretion delay, Nonlinear Dynamics, 2011, 63(3), 417–427. doi: 10.1007/s11071-010-9812-5 [30] Y. H. Peng and G. Y. Zhang, Dynamics analysis of a predator-prey model with herd behavior and nonlocal prey competition, Mathematics and Computers in Simulation, 2020, 170, 366–378. doi: 10.1016/j.matcom.2019.11.012 [31] Z. L. Shen and C. R. Zhang, Double Hopf bifurcation of coupled dissipative Stuart-Landau oscillators with delay, Applied Mathematics and Computation, 2014, 227, 553–566. doi: 10.1016/j.amc.2013.11.044 [32] G. T. Skalski and J. F. Gilliam, Functional responses with predator interference: Viable alternatives to the Holling type II model, Ecology, 2001, 82(11), 3083–3092. doi: 10.1890/0012-9658(2001)082[3083:FRWPIV]2.0.CO;2 [33] F. Souna, S. Djilali, S. Alyobi, A. Zeb, N. Gul, S. Alsaeed and K. S. Nisar, Spatiotemporal dynamics of a diffusive predator-prey system incorporating social behavior, AIMS Mathematics, 2023, 8(7), 15723–15748. doi: 10.3934/math.2023803 [34] F. Wang and R. Yang, Spatial pattern formation driven by the cross-diffusion in a predator-prey model with Holling type functional response, Chaos, Solitons and Fractals, 2023, 174, 113890. doi: 10.1016/j.chaos.2023.113890 [35] F. Wang and R. Yang, Dynamics of a delayed reaction-diffusion predator-prey model with nonlocal competition and double Allee effect in prey, International Journal of Biomathematics, 2025, 18(02), 2350097. doi: 10.1142/S1793524523500973 [36] F. Wang, R. Yang and X. Zhang, Turing patterns in a predator-prey model with double Allee effect, Mathematics and Computers in Simulation, 2024, 220, 170–191. doi: 10.1016/j.matcom.2024.01.015 [37] J. Wang, J. Shi and J. Wei, Dynamics and pattern formation in a diffusive predator-prey system with strong Allee effect in prey, Journal of Differential Equations, 2011, 251(4–5), 1276–1304. doi: 10.1016/j.jde.2011.03.004 [38] L. Y. Wang, W. L. Wang and R. Z. Yang, Stability switch and Hopf bifurcations for a diffusive plankton system with nonlocal competition and toxic effect, AIMS Mathematics, 2023, 8(4), 9716–9739. doi: 10.3934/math.2023490 [39] T. P. Weng, Stability analysis of diffusive predator-prey model with modified Leslie-Gower and Holling-type III schemes, Applied Mathematics and Computation, 2011, 218(7), 3733–3745. doi: 10.1016/j.amc.2011.09.018 [40] J. Xu and L. J. Pei, The nonresonant double Hopf bifurcation in delayed neural network, International Journal of Computer Mathematics, 2008, 85(6), 925–935. doi: 10.1080/00207160701405469 [41] R. Yang and C. Zhang, Dynamics in a diffusive predator prey system with a constant prey refuge and delay, Nonlinear Analysis Real World Applications, 2016, 31, 1–22. doi: 10.1016/j.nonrwa.2016.01.005 [42] W. Yang, Global asymptotical stability and persistent property for a diffusive predator-prey system with modified Leslie-Gower functional response, Nonlinear Analysis-Real World Applications, 2013, 14(3), 1323–1330. doi: 10.1016/j.nonrwa.2012.09.020 [43] F. Yi, J. Wei and J. Shi, Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator-prey system, Journal of Differential Equations, 2009, 246(5), 1944–1977. doi: 10.1016/j.jde.2008.10.024 [44] J. You and G. Guo, Pattern formation for a reversible biochemical reaction model with cross-diffusion and Michalis saturation, Journal of Mathematical Chemistry, 2025. DOI: 10.1007/s10910-025-01705-0. [45] Y. Zhang and J. Xu, Classification and computation of non-resonant double Hopf bifurcations and solutions in delayed van der Pol-Duffing system, International Journal of Nonlinear Sciences and Numerical Simulation, 2005, 6(1), 63–68. [46] F. Zhu and R. Yang, Bifurcation in a modified Leslie-Gower model with nonlocal competition and fear effect, Discrete and Continuous Dynamical Systems - B, 2025. DOI: 10.3934/dcdsb.2024195. -
-
Figures(7) / Tables(4)
Export File
Citation
Yuxin Ma, Ruizhi Yang. BIFURCATION ANALYSIS IN A MODIFIED LESLIE-GOWER WITH NONLOCAL COMPETITION AND BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2152-2184. doi: 10.11948/20240415
Format
Content
DownLoad:
-
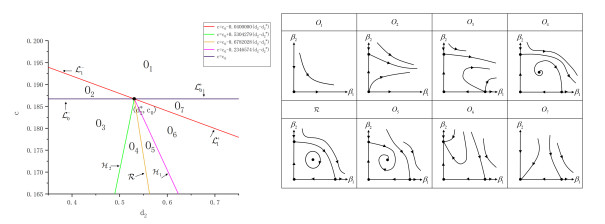
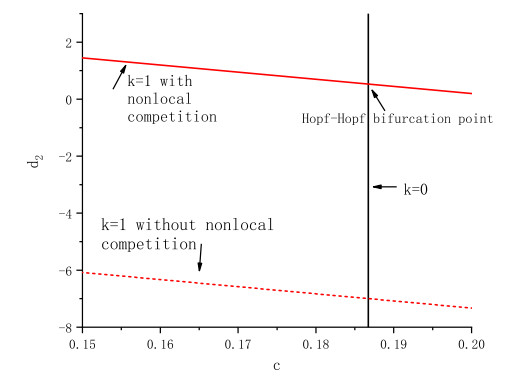
Figure 1.
Hopf bifurcation curves of models with and without nonlocal competition.
-
Figure 2.
Left: the bifurcation regions of the system (5.1) near
$ ({d_2}^*, c_0 ) $ $ (d_2, c) $ $ O_1 $ $ O_7 $ $ \mathcal{R} $ -
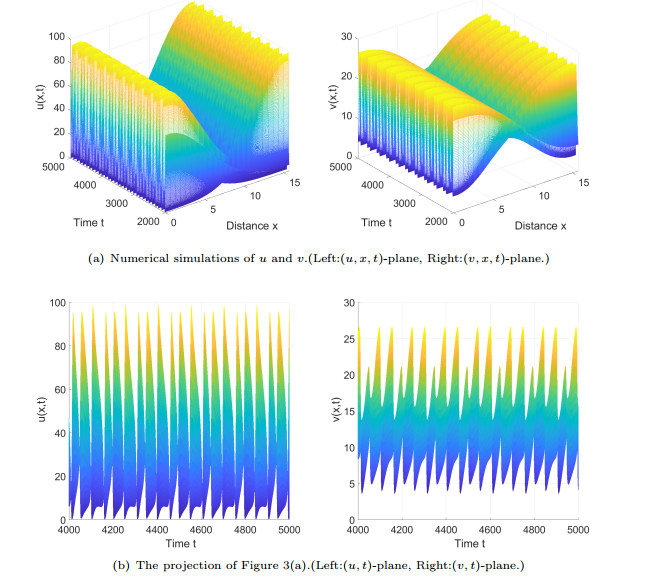
Figure 3.
Numerical simulations of (1.4) for parameters
$ (d_2,c)=(0.7707693, $ $ 0.00267237)\in {O_5} $ $ u(x,0)=u^*+0.0045000cos(\frac{3}{5}x) $ $ v(x,0)=v^*+0.0005000cos(\frac{3}{5}x) $ $ O_5 $ -
Figure 4.
Numerical simulations of the system without nonlocal competition for parameters
$ (d_2,c)=(0.7707693,0.00267237)\in {O_5} $ $ u(x,0)=u^*+0.0045000cos(\frac{3}{5}x) $ $ v(x,0)=v^*+0.0005000cos(\frac{3}{5}x) $ $ (u,x,t) $ $ (v,x,t) $ $ O_5 $ -
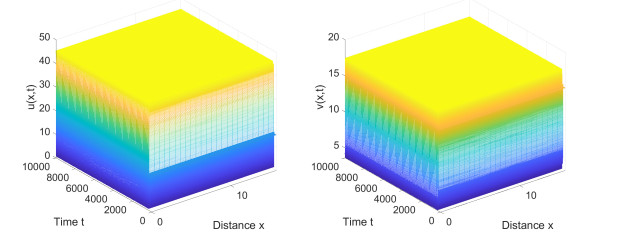
Figure 5.
Numerical simulations of (1.4) for parameters
$ (d_2,c)=(0.5807693, $ $ 0.1857237) \in {O_6} $ $ u(x,0)=u^*+0.0004000cos(\frac{2}{5}x) $ $ v(x,0)=v^*+0.0002000cos(\frac{2}{5}x) $ $ O_6 $ -
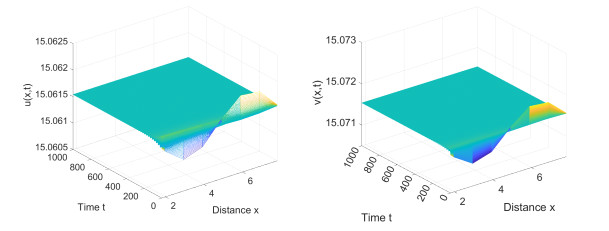
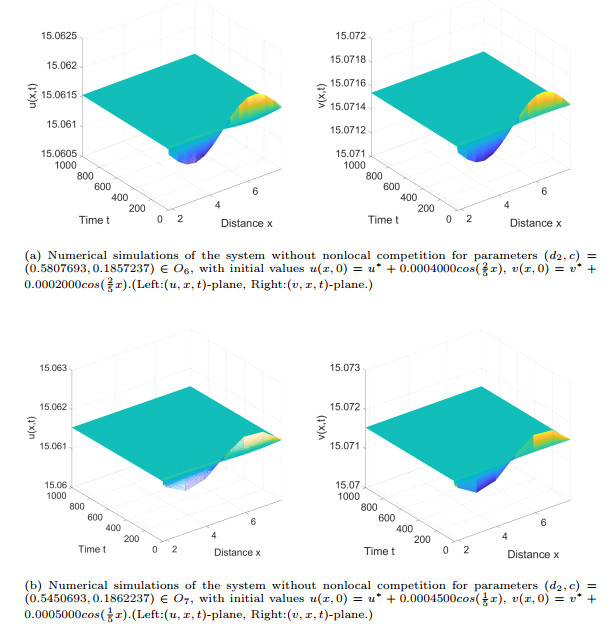
Figure 6.
Numerical simulations of (1.4) for parameters
$ (d_2,c)=(0.5450693, $ $ 0.1862237)\in {O_7} $ $ u(x,0)=u^*+0.0004500cos(\frac{1}{5}x) $ $ v(x,0)=v^*+0.0005000cos(\frac{1}{5}x) $ $ (u,x,t) $ $ (v,x,t) $ $ O_7 $ -
Figure 7.
Numerical simulations of the system without nonlocal competition for parameters in
$ O_6 $ $ O_7 $ $ O_6 $ $ O_7 $