| Citation: |
Mo Faheem, Arshad Khan, Fathalla Ali Rihan. A WAVELET COLLOCATION METHOD FOR NEUTRAL DELAY DIFFERENTIAL EQUATIONS ON METRIC STAR GRAPH[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2124-2151. doi: 10.11948/20240402
|
A WAVELET COLLOCATION METHOD FOR NEUTRAL DELAY DIFFERENTIAL EQUATIONS ON METRIC STAR GRAPH
-
Abstract
This paper proposes a Haar wavelet collocation approach to solve neutral delay differential equations on a metric star graph (NDDE-MSG) with $\kappa$ edges. The application of Haar wavelet, together with its integration on NDDE-MSG, yields a system of equations, which on solving gives unknown wavelet coefficients and subsequently the solution. The upper bound of the global error norm is established to demonstrate that the proposed method converges exponentially. We conduct some numerical experiments to test the computational convergence of our approach. In this study, the authors explore the numerical solution for NDDE on metric star graphs for the first time.
-
-
References
[1] J.-P. Antoine, R. Murenzi, P. Vandergheynst and S. T. Ali, Two-Dimensional Wavelets and their Relatives, Cambridge University Press, 2008. [2] H. Azin, M. Heydari, O. Baghani and F. Mohammadi, Fractional Vieta-Fibonacci wavelets: Application for systems of fractional delay differential equations, Physica Scripta, 2023, 98(9), 095242. doi: 10.1088/1402-4896/aceec0 [3] T. Dumrongpokaphan, Y. Lenbury, R. Ouncharoen and Y. Xu, An intracellular delay-differential equation model of the HIV infection and immune control, Math. Modell. Natural Phenom., 2007, 2(1), 84–112. doi: 10.1051/mmnp:2008012 [4] A. Abou-El-Ela, A. Sadek and A. Mahmoud, Existence and uniqueness of a periodic solution for third-order delay differential equation with two deviating arguments, IAENG Int. J. Appl. Math., 2012, 42(1), 7–12. [5] M. Faheem and A. Khan, A collocation method for time-fractional diffusion equation on a metric star graph with $\eta$ edges, Math. Meth. Appl. Sci., 2023, 46(8), 8895–8914. doi: 10.1002/mma.9023 [6] M. Faheem, A. Khan and Ö. Oruç, A generalized Gegenbauer wavelet collocation method for solving p-type fractional neutral delay differential and delay partial differential equations, Math. Sci., 2024, 18, 137–166. doi: 10.1007/s40096-022-00490-0 [7] M. Faheem, A. Raza and A. Khan, Collocation methods based on Gegenbauer and Bernoulli wavelets for solving neutral delay differential equations, Math. Comput. Simul., 2020, 180, 72–92. [8] U. Ghosh, S. Chowdhury and D. K. Khan, Mathematical modelling of epidemiology in presence of vaccination and delay, Comput. Sci. Infor. Tech. (CS and IT), 2013, 91–98. [9] K. Gopalsamy, Stability and Oscillations in Delay Differential Equations of Population Dynamics, 74, Springer Science & Business Media Dordrecht, 2013. [10] J. R. Graef, M. K. Grammatikopoulos and P. W. Spikes, On the asymptotic behavior of solutions of a second order nonlinear neutral delay differential equation, Jour. Math. Anal. Appl., 1991, 156(1), 23–39. doi: 10.1016/0022-247X(91)90379-E [11] M. H. Heydari and O. Bavi, An efficient wavelet method for nonlinear problems arising in heat transfer, Eng. Comput., 2022, 38(4), 2867–2878. [12] M. H. Heydari and M. Razzaghi, A hybrid method based on the Chebyshev cardinal functions/wavelets for time fractional coupled Klein–Gordon–Schrödinger equations, Jour. Comput. Appl. Math., 2023, 427, 115142. doi: 10.1016/j.cam.2023.115142 [13] M. H. Heydari and M. Razzaghi, A new wavelet method for fractional integro-differential equations with $\psi$-Caputo fractional derivative, Math. Comput. Simul., 2024, 217, 97–108. doi: 10.1016/j.matcom.2023.10.023 CrossRef $\psi$-Caputo fractional derivative" target="_blank">Google Scholar
[14] M. H. Heydari, M. Razzaghi and C. Cattani, Fractional Chebyshev cardinal wavelets: Application for fractional quadratic integro-differential equations, Inter. Jour. Comput. Math., 2023, 100(3), 479–496. doi: 10.1080/00207160.2022.2122052 [15] A. Hussain and T. Kanwal, Existence and uniqueness for a neutral differential problem with unbounded delay via fixed point results, Trans. A. Razmadze Math. Inst., 2018, 172(3), 481–490. doi: 10.1016/j.trmi.2018.08.006 [16] T. Insperger, On the approximation of delayed systems by Taylor series expansion, Jour. Comput. Nonlinear Dyn., 2015, 10(2), 024503. doi: 10.1115/1.4027180 [17] Z. Jackiewicz, Existence and uniqueness of solutions of neutral delay-differential equations with state dependent delays, Funkcial. Ekvac, 1987, 30(1), 9–17. [18] G. Kron, Electric circuit models of the Schrödinger equation, Phys. Rev., 1945, 67(1–2), 39. doi: 10.1103/PhysRev.67.39 [19] J. E. Lagnese and G. Leugering, Domain in Decomposition Methods in Optimal Control of Partial Differential Equations, 148, Springer Science & Business Media, 2004. [20] G. Leugering, Dynamic domain decomposition of optimal control problems for networks of strings and Timoshenko beams, SIAM J. Contr. Optim., 1999, 37(6), 1649–1675. doi: 10.1137/S0363012997331986 [21] M. Mehra, A. Shukla and G. Leugering, An adaptive spectral graph wavelet method for PDEs on networks, Adv. Comput. Math., 2021, 47(1), 1–29. doi: 10.1007/s10444-020-09827-6 [22] D. Mugnolo, Semigroup Methods for Evolution Equations on Networks, 20, Springer, 2014. [23] Ö. Oruç, Integrated Chebyshev wavelets for numerical solution of nonlinear one-dimensional and two-dimensional Rosenau equations, Wave Motion, 2023, 118, 103107. doi: 10.1016/j.wavemoti.2022.103107 [24] P. Rahimkhani, Y. Ordokhani and S. Sabermahani, Bernoulli wavelet least squares support vector regression: Robust numerical method for systems of fractional differential equations, Math. Meth. Appl. Sci., 2023, 46(17), 17641–17659. doi: 10.1002/mma.9522 [25] A. Raza, A. Khan, P. Sharma and K. Ahmad, Solution of singularly perturbed differential difference equations and convection delayed dominated diffusion equations using Haar wavelet, Math. Sci., 2021, 15(2), 123–136. doi: 10.1007/s40096-020-00355-4 [26] F. A. Rihan, Delay Differential Equations and Applications to Biology, Springer (SP), 2021. https://doi.org/10.1007/978-981-16-0626-7. doi: 10.1007/978-981-16-0626-7 [27] K. Ruedenberg and C. W. Scherr, Free-electron network model for conjugated systems, I. Theory, The Jour. Chem. Phy., 1953, 21(9), 1565–1581. doi: 10.1063/1.1699299 [28] S. Sabermahani, Y. Ordokhani and P. Rahimkhani, Application of generalized Lucas wavelet method for solving nonlinear fractal-fractional optimal control problems, Chaos, Solitons & Fractals, 2023, 170, 113348. [29] S. Sabermahani, Y. Ordokhani and M. Razzaghi, Ritz-generalized Pell wavelet method: Application for two classes of fractional pantograph problems, Commun. Nonlinear Sci. Numer. Simul., 2023, 119, 107138. doi: 10.1016/j.cnsns.2023.107138 [30] A. Shukla, M. Mehra and G. Leugering, A fast adaptive spectral graph wavelet method for the viscous Burgers' equation on a star-shaped connected graph, Math. Meth. Appl. Sci., 2020, 43(13), 7595–7614. doi: 10.1002/mma.5907 [31] M. C. Steinbach, On PDE solution in transient optimization of gas networks, Jour. Comput. Appl. Math., 2007, 203(2), 345–361. doi: 10.1016/j.cam.2006.04.018 [32] D. F. Walnut, An Introduction to Wavelet Analysis, Springer Science & Business Media, 2002. [33] H. Yoshioka, K. Unami and M. Fujihara, Burgers type equation models on connected graphs and their application to open channel hydraulics (mathematical aspects and applications of nonlinear wave phenomena), Kyuto Uni., 2014, 1890, 160–171. -
-
Figures(8) / Tables(5)
Export File
Citation
Mo Faheem, Arshad Khan, Fathalla Ali Rihan. A WAVELET COLLOCATION METHOD FOR NEUTRAL DELAY DIFFERENTIAL EQUATIONS ON METRIC STAR GRAPH[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2124-2151. doi: 10.11948/20240402
Format
Content
DownLoad:
-
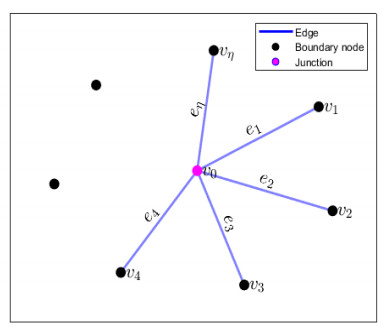
Figure 1.
Simplified schematic representation of a metric star graph consisting
$ \kappa $ -
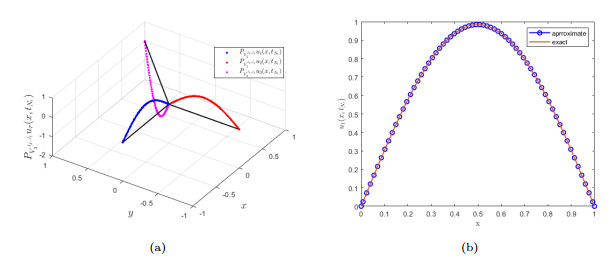
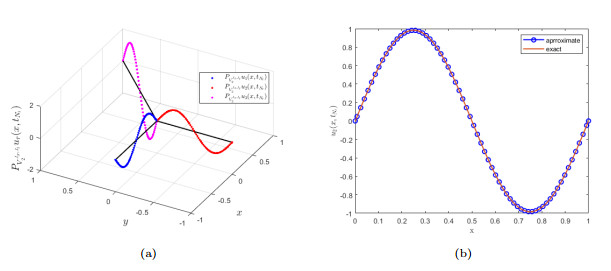
Figure 2.
(2(a)) Graph of
$ P_{V_{2}^{J_{\mathit{x}}, J_{\mathit{t}}}}u_{r}(\mathit{x, t}), \;r=1, 2, 3 $ $ \mathit{t}=\mathit{t}_{N_{\mathit{t}}} $ $ J_{\mathit{x}}=J_{\mathit{t}}=5 $ $ u_{1}(\mathit{x, t}) $ $ \mathit{t}=\mathit{t}_{N_{\mathit{t}}} $ $ J_{\mathit{x}}=J_{\mathit{t}}=5 $ -
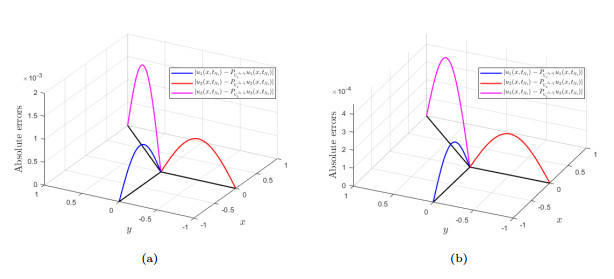
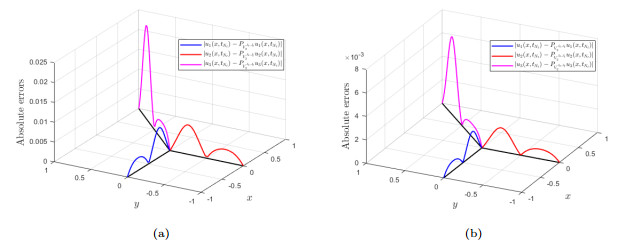
Figure 3.
Impact of resolution parameters
$ J_{\mathit{x}}, \;J_{\mathit{t}} $ $ u(\mathit{x, t}) $ $ \mathit{t}=\mathit{t}_{N_{\mathit{t}}} $ $ J_{\mathit{x}}=J_{\mathit{t}}=4 $ $ J_{\mathit{x}}=J_{\mathit{t}}=5 $ -
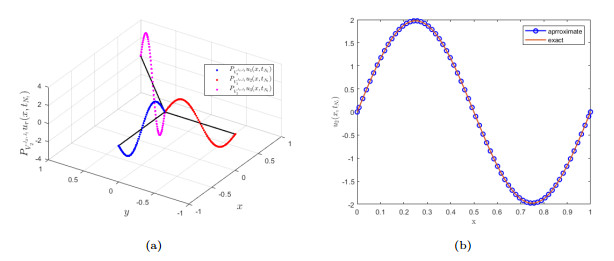
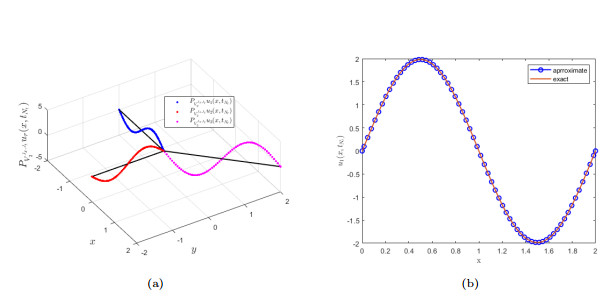
Figure 4.
(4(a)) Graph of
$ P_{V_{2}^{J_{\mathit{x}}, J_{\mathit{t}}}}u_{r}(\mathit{x, t}), \;r=1, 2, 3 $ $ \mathit{t}=\mathit{t}_{N_{\mathit{t}}} $ $ J_{\mathit{x}}=J_{\mathit{t}}=5 $ $ u_2(\mathit{x, t}) $ $ \mathit{t}=\mathit{t}_{N_{\mathit{t}}} $ $ J_{\mathit{x}}=J_{\mathit{t}}=5 $ -
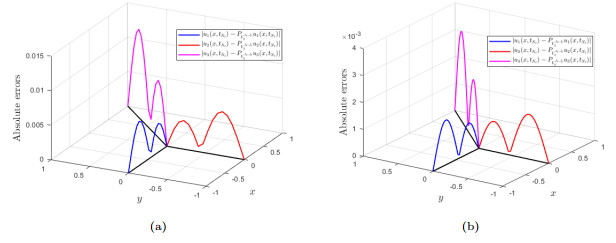
Figure 5.
Impact of resolution parameters
$ J_{\mathit{x}}, \;J_{\mathit{t}} $ $ u(\mathit{x, t}) $ $ \mathit{t}=\mathit{t}_{N_{\mathit{t}}} $ $ J_{\mathit{x}}=J_{\mathit{t}}=3 $ $ J_{\mathit{x}}=J_{\mathit{t}}=4 $ -
Figure 6.
(6(a)) Graph of
$ P_{V_{2}^{J_{\mathit{x}}, J_{\mathit{t}}}}u_{r}(\mathit{x, t}), \;r=1, 2, 3 $ $ \mathit{t}=\mathit{t}_{N_{\mathit{t}}} $ $ J_{\mathit{x}}=J_{\mathit{t}}=5 $ $ u_2(\mathit{x, t}) $ $ \mathit{t}=\mathit{t}_{N_{\mathit{t}}} $ $ J_{\mathit{x}}=J_{\mathit{t}}=5 $ -
Figure 7.
Impact of resolution parameters
$ J_{\mathit{x}}, \;J_{\mathit{t}} $ $ u(\mathit{x, t}) $ $ \mathit{t}=\mathit{t}_{N_{\mathit{t}}} $ $ J_{\mathit{x}}=J_{\mathit{t}}=4 $ $ J_{\mathit{x}}=J_{\mathit{t}}=5 $ -
Figure 8.
(8(a)) Graph of
$ P_{V_{2}^{J_{\mathit{x}}, J_{\mathit{t}}}}u_{r}(\mathit{x, t}), \;r=1, 2, 3 $ $ \mathit{t}=\mathit{t}_{N_{\mathit{t}}} $ $ J_{\mathit{x}}=J_{\mathit{t}}=5 $ $ u_{1}(\mathit{x, t}) $ $ \mathit{t}=\mathit{t}_{N_{\mathit{t}}} $ $ J_{\mathit{x}}=J_{\mathit{t}}=5 $