| Citation: |
Changbum Chun, Beny Neta. COMPARATIVE STUDY OF METHODS OF VARIOUS ORDERS FOR FINDING SIMPLE ROOTS OF NONLINEAR EQUATIONS[J]. Journal of Applied Analysis & Computation, 2019, 9(2): 400-427. doi: 10.11948/2156-907X.20160229
|
COMPARATIVE STUDY OF METHODS OF VARIOUS ORDERS FOR FINDING SIMPLE ROOTS OF NONLINEAR EQUATIONS
-
Abstract
Recently there were many papers discussing the basins of attraction of various methods and ideas how to choose the parameters appearing in families of methods and weight functions used. Here we collected many of the results scattered and put a quantitative comparison of methods of orders from 2 to 7. We have used the average number of function-evaluations per point, the CPU time and the number of black points to compare the methods. We also include the best eighth order method. Based on 7 examples, we show that there is no method that is best based on the 3 criteria. We found that the best eighth order method, SA8, and CLND are at the top.-
Keywords:
- Iterative methods /
- nonlinear equations /
- simple roots /
- order of convergence /
- basin of attraction
-
-
References
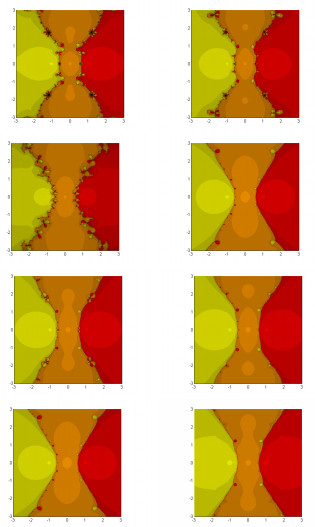
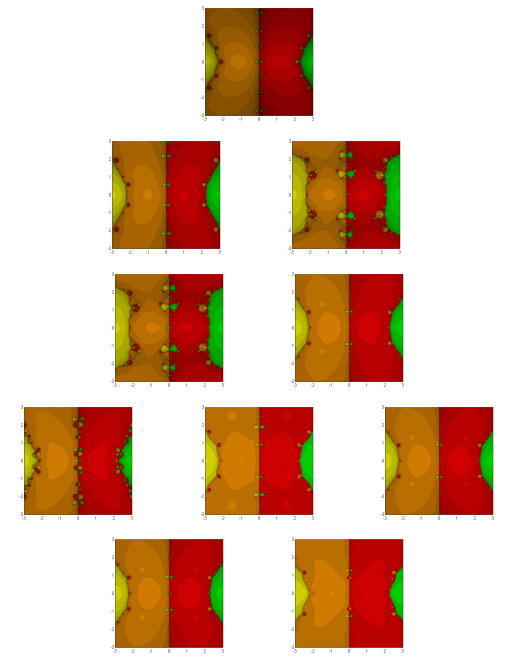
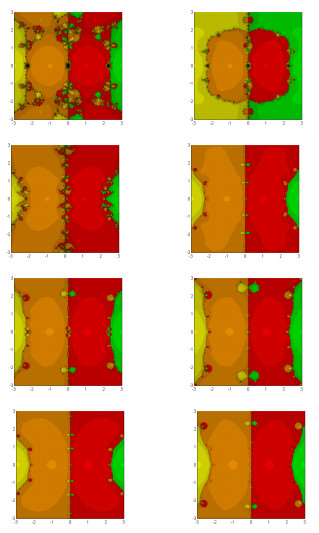
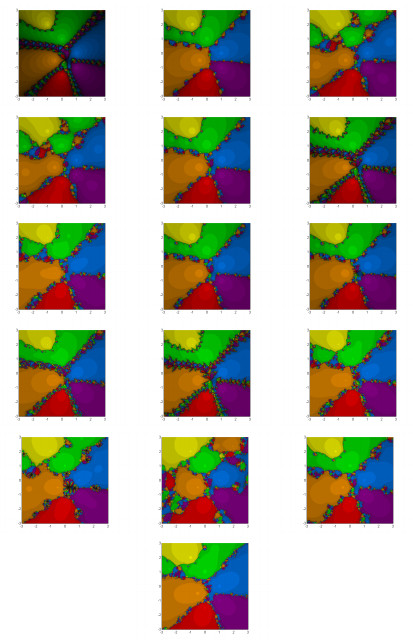
[1] S. Amat, S. Busquier and S. Plaza, Review of some iterative root-finding methods from a dynamical point of view, Scientia, 2004, 10, 3–35. [2] S. Amat, S. Busquier and S. Plaza, Dynamics of a family of third-order iterative methods that do not require using second derivatives, Appl. Math. Comput., 2004, 154, 735–746. [3] S. Amat, S. Busquier and S. Plaza, Dynamics of the King and Jarratt iterations, Aeq. Math., 2005, 69, 212–2236. doi: 10.1007/s00010-004-2733-y [4] I. K. Argyros and A. A. Magreñan, On the convergence of an optimal fourth-order family of methods and its dynamics, Appl. Math. Comput., 2015, 252, 336–346. [5] D. K. R. Babajee, A. Cordero, F. Soleymani and J. R. Torregrosa, On improved three-step schemes with high efficiency index and their dynamics, Numer. Algorithms, 2014, 65, 153–169. doi: 10.1007/s11075-013-9699-6 [6] M. Basto, V. Semiao and F. Calheiros, A new iterative method to compute nonlinear equations, Appl. Math. Comput., 2006, 173, 468–483. [7] W. Bi, H. Ren and Q. Wu, New family of seventh-order methods for nonlinear equations, Appl. Math. Comput., 2008, 203, 408–412. [8] W. Bi, H. Ren and Q. Wu, Three-step iterative methods with eight-order convergence for solving nonlinear equations, J. Comput. Appl. Math., 2009, 225, 105–112. doi: 10.1016/j.cam.2008.07.004 [9] W. Bi, Q. Wu and H. Ren, A new family of eight-order iterative methods for solving nonlinear equations, Appl. Math. Comput. 2009, 214, 236–245. [10] C. Chun, M. Y. Lee, B. Neta and J. Džunić, On optimal fourth-order iterative methods free from second derivative and their dynamics, Appl. Math. Comput., 2012, 218, 6427–6438. [11] C. Chun, B. Neta and Sujin Kim, On Jarratt's family of optimal fourth-order iterative methods and their dynamics, Fractals, 2014. DOI:10.1142/S0218348X14500133. [12] C. Chun and B. Neta, On the new family of optimal eighth order methods developed by Lotfi et al., Numer. Algorithms, 2016, 72, 363–376. doi: 10.1007/s11075-015-0048-9 [13] C. Chun and B. Neta, Comparison of several families of optimal eighth order methods, Appl. Math. Comput., 2016, 274, 762–773. [14] C. Chun and B. Neta, The basins of attraction of Murakami's fifth order family of methods, Appl. Numer. Math., 2016, 110, 14–25. doi: 10.1016/j.apnum.2016.07.012 [15] C. Chun and B. Neta, An analysis of a new family of eighth-order optimal methods, Appl. Math. Comput., 2014, 245, 86–107. [16] C. Chun and B. Neta, An analysis of a King-based family of optimal eighth-order methods, Amer. J. Algorithms and Computing, 2015, 2, 1–17. [17] C. Chun, B. Neta, J. Kozdon and M. Scott, Choosing weight functions in iterative methods for simple roots, Appl. Math. Comput., 2014, 227, 788–800. [18] C. Chun and B. Neta, Basin of attraction for several third order methods to find multiple roots of nonlinear equations, Appl. Math. Comput., 2015, 268, 129–137. [19] C. Chun and B. Neta, Comparative study of eighth order methods for finding simple roots of nonlinear equations, Numer. Algorithms, 2017, 74(4), 1169–1201. doi: 10.1007/s11075-016-0191-y [20] C. Chun and B. Neta, Comparing the basins of attraction for Kanwar-Bhatia-Kansal family to the best fourth order method, Appl. Math. Comput., 2015, 266, 277–292. [21] C. Chun and Y. Ham, Some second-derivative-free variants of super-Halley method with fourth-order convergence, Appl. Math. Comput., 2008, 195, 537–541. [22] C. Chun and B. Neta, An analysis of a Kharrri's 4th order family of methods, Appl. Math. Comput., 2016, 279, 198–207. [23] C. Chun and B. Neta, A new sixth-order scheme for nonlinear equations, Appl. Math. Lett., 2012, 25, 185–189. doi: 10.1016/j.aml.2011.08.012 [24] C. Chun and B. Neta, An analysis of a family of Maheshwari-based optimal eighth-order methods, Appl. Math. Comput., 2015, 253, 294–307. [25] C. Chun and M. Y. Lee, A new optimal eighth-order family of iterative methods for the solution of nonlinear equations, Appl. Math. Comput., 2013, 223, 506–519. [26] F. Chicharro, A. Cordero, J. M. Gutiérrez and J. R. Torregrosa, Complex dynamics of derivative-free methods for nonlinear equations, Appl. Math. Comput., 2013, 219, 7023–7035. [27] A. Cordero, J., García-Maimó, J. R. Torregrosa, M. P. Vassileva and P. Vindel, Chaos in King's iterative family, Appl. Math. Lett., 2013, 26, 842–848. doi: 10.1016/j.aml.2013.03.012 [28] A. Cordero, M. Fardi, M. Ghasemi and J. R. Torregrosa, Accelerated iterative methods for finding solutions of nonlinear equations and their dynamical behavior, Calcolo, 2014, 51, 17–30. doi: 10.1007/s10092-012-0073-1 [29] A. Cordero, J. Torregrosa and M. Vassileva, Three-step iterative methods with optimal eighth-order convergence, J. Comput. Appl. Math., 2011, 235, 3189–3194. doi: 10.1016/j.cam.2011.01.004 [30] Y. H. Geum, Y. I. Kim and B. Neta, On developing a higher-order family of double-Newton methods with a bivariate weighting function, Appl. Math. Comput., 2015, 254, 277–290. [31] Y. H. Geum, Y. I. Kim and B. Neta, A class of two-point sixth-order multiple-zero finders of modified double-Newton type and their dynamics, Appl. Math. Comput., 2015, 270, 387–400. [32] Y. H. Geum, Y. I. Kim and B. Neta, A family of optimal quartic-order multiple-zero finders with a weight function of the principal kth root of a derivative-to-derivative ratio and their basins of attraction, Math. Comput. Simulat., 2017, 136, 1–21. doi: 10.1016/j.matcom.2016.10.008 [33] Y. H. Geum, Y. I. Kim, A and A. Magreñan, A biparametric extension of King's fourth-order methods and their dynamics, Appl. Math. Comput., 2016, 282, 254–275. [34] J. M. Gutiérrez and M. A. Hernández, An acceleration of Newton's method: Super-Halley method, Appl. Math. Comput., 2001, 117, 223–239. [35] E. Halley, A new, exact and easy method of finding the roots of equations generally and that without any previous reduction, Phil. Trans. Roy. Soc. London, 1694, 18, 136–148. doi: 10.1098/rstl.1694.0029 [36] E. Hansen and M. Patrick, A family of root finding methods, Numer. Math., 1977, 27, 257–269. [37] A. S. Householder, The Numerical Treatment of a Single Equation, McGraw-Hill, New York, NY, 1970. [38] P. Jarratt, Some efficient fourth-order multipoint methods for solving equations, BIT, 1969, 9, 119–124. doi: 10.1007/BF01933248 [39] P. Jarratt, Some fourth-order multipoint iterative methods for solving equations, Math. Comput., 1966, 20, 434–437. doi: 10.1090/S0025-5718-66-99924-8 [40] Y. Khan, M. Fardi and K. Sayevand, A new general eighth-order family of iterative methods for solving nonlinear equations, App. Math. Lett., 2012, 25, 2262–2266. doi: 10.1016/j.aml.2012.06.014 [41] S. K. Khattri and D. K. R. Babajee, Fourth-order family of iterative methods with four parameters, International J. of Mathematics and Computation, 2013, 19, 1–10. [42] R. F. King, A family of fourth-order methods for nonlinear equations, SIAM Numer. Anal., 1973, 10, 876–879. doi: 10.1137/0710072 [43] J. Kou, Y. Li and X. Wang, Fourth-order iterative methods free from second derivative, Appl. Math. Comput., 2007, 184, 880–885. [44] H. T. Kung and J. F. Traub, Optimal order of one-point and multipoint iterations, J. Assoc. Comput. Mach., 1974, 21, 643–651. doi: 10.1145/321850.321860 [45] T. Lotfi, S. Sharifi, M. Salimi and S. Siegmund, A new class of three-point methods with optimal convergence order eight and its dynamics, Numer. Algorithms, 2015, 68, 261–288. doi: 10.1007/s11075-014-9843-y [46] A. A. Magreñan, Different anomalies in a Jarratt family of iterative root-finding methods, Appl. Math. Comput., 2014, 233, 29–38. [47] A. K. Maheshwari, A fourth-order iterative method for solving nonlinear equations, Appl. Math. Comput., 2009, 211, 383–391. [48] T. Murakami, Some fifth order multipoint iterative formulae for solving equations, J. of Information Processing, 1978, 1, 138–139. [49] B. Neta, M. Scott and C. Chun, Basin of attractions for several methods to find simple roots of nonlinear equations, Appl. Math. Comput., 2012, 218, 10548–10556. [50] B. Neta, C. Chun and M. Scott, Basins of attractions for optimal eighth order methods to find simple roots of nonlinear equations, Appl. Math. Comput., 2014, 227, 567–592. [51] B. Neta, M. Scott and C. Chun, Basin attractors for various methods for multiple roots, Appl. Math. Comput., 2012, 218, 5043–5066. [52] B. Neta and C. Chun, On a family of Laguerre methods to find multiple roots of nonlinear equations, Appl. Math. Comput., 2013, 219, 10987–11004. [53] B. Neta and C. Chun, Basins of attraction for several optimal fourth order methods for multiple roots, Math. Comput. Simulat., 2014, 103, 39–59. doi: 10.1016/j.matcom.2014.03.007 [54] B. Neta and C. Chun, Basins of attraction for Zhou-Chen-Song fourth order family of methods for multiple roots, Math. Comput. Simulat., 2015, 109, 74–91. doi: 10.1016/j.matcom.2014.08.005 [55] B. Neta, C. Chun and M. Scott, A note on the modified super-Halley method, Appl. Math. Comput., 2012, 218, 9575–9577. [56] B. Neta, A sixth order family of methods for nonlinear equations, Int. J. Computer Math., 1979, 7, 157–161. doi: 10.1080/00207167908803166 [57] B. Neta and A. N. Johnson, High order nonlinear solver, J. Comput. Methods Science and Engineering, 2008, 8(4-6), 245–250. [58] B. Neta and M. S. Petković, Construction of optimal order nonlinear solvers using inverse interpolation, Appl. Math. Comput., 2010, 217, 2448–2455. [59] B. Neta, On a family of multipoint methods for nonlinear equations, Int. J. Computer Math., 1981, 9, 353–361. doi: 10.1080/00207168108803257 [60] A. M. Ostrowski, Solution of Equations and Systems of Equations, 3rd ed. Academic Press, New York London, 1973. [61] M. S. Petković, B. Neta, L. D. Petković, J. Džunić, Multipoint Methods for Solving Nonlinear Equations, Elsevier, 2013. [62] D. B. Popovski, A family of one point iteration formulae for finding roots, Int. J. Computer Math., 1980, 8, 85–88. doi: 10.1080/00207168008803193 [63] M. Scott, M, B. Neta and C. Chun, Basin attractors for various methods, t Appl. Math. Comput., 2011, 218, 2584–2599. doi: 10.1016/j.amc.2011.07.076 [64] J. R. Sharma and R. Sharma, A new family of modified Ostrowski's methods with accelerated eighth order convergence, Numer. Algorithms, 2010, 54, 445–458. doi: 10.1007/s11075-009-9345-5 [65] J. R. Sharma and H. Arora, A new family of optimal eighth order methods with dynamics for nonlinear equations, Appl. Math. Comput., 2016, 273, 924–933. [66] B. D. Stewart, Attractor Basins of Various Root-Finding Methods, M. S. thesis, Naval Postgraduate School, Department of Applied Mathematics, Monterey, CA, June 2001. [67] R. Thukral and M. S. Petković, Family of three-point methods of optimal order for solving nonlinear equations, J. Comput. Appl. Math., 2010, 233, 2278–2284. doi: 10.1016/j.cam.2009.10.012 [68] J. F. Traub, Iterative Methods for the Solution of Equations, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1964. [69] X. Wang and L. Liu, Modified Ostrowski's method with eighth-order convergence and high efficiency index, Appl. Math. Lett., 2010, 23, 549–554. doi: 10.1016/j.aml.2010.01.009 [70] X. Wang and L. Liu, New eighth-order iterative methods for solving nonlinear equations, J. Comput. Appl. Math., 2010, 234, 1611–1620. doi: 10.1016/j.cam.2010.03.002 -
-
Figures(12) / Tables(6)
Export File
Citation
Changbum Chun, Beny Neta. COMPARATIVE STUDY OF METHODS OF VARIOUS ORDERS FOR FINDING SIMPLE ROOTS OF NONLINEAR EQUATIONS[J]. Journal of Applied Analysis & Computation, 2019, 9(2): 400-427. doi: 10.11948/2156-907X.20160229
Format
Content
DownLoad:
-
Figure 1. The top row for Newton. Second row for Halley (left), Euler-Chebyshev (center) and BSC (right). Third row for Super Halley (left), King with
$ \beta = 3-2\sqrt{2} $ (center), and Ostrowski (right). Fourth row for Kung-Traub fourth order (left), Maheshwari (center), and JHIF4 (right). Bottom row for CLND (left), KB74 (center) and Murakami (right) for the roots of the polynomial$ z^2-1 $ . -
Figure 2. The top row for Neta sixth order with
$ \beta = -1/2 $ (left) and N6d (right). Second row for CN6 (left) and WL6 (right). Third row for NIK7 (left), and NIK7d (right) and bottom row for JHID7 (left), BRW7 (center) and SA8 (right) for the roots of the polynomial$ z^2-1 $ . -
Figure 3. The top row for Newton. Second row for Halley (left), Euler-Chebyshev (center) and BSC (right). Third row for Super Halley (left), King with
$ \beta = 3-2\sqrt{2} $ (center), and Ostrowski (right). Fourth row for Kung-Traub fourth order (left), Maheshwari (center), and JHIF4 (right). Bottom row for CLND (left), KB74 (center) and Murakami (right) for the roots of the polynomial$ z^3-1 $ . -
Figure 4. The top row for Neta sixth order with
$ \beta = -1/2 $ (left) and N6d (right). Second row for CN6 (left) and WL6 (right). Third row for NIK7 (left) and NIK7d right) and bottom row for JHID7 (left), BRW7 (center) and SA8 (right) for the roots of the polynomial$ z^3-1 $ . -
Figure 5. The top row for Newton. Second row for Halley (left), Euler-Chebyshev (center) and BSC (right). Third row for Super Halley (left), King with
$ \beta = 3-2\sqrt{2} $ (center), and Ostrowski (right). Fourth row for Kung-Traub fourth order (left), JHIF4 (center) and CLND (right). Bottom row for KB74 (left) and Murakami (right) for the roots of the polynomial$ z^3-z $ . -
Figure 6. The top row for Neta sixth order with
$ \beta = -1/2 $ (left) and N6d (right). Second row for CN6 (left) and WL6 (right). Third row for NIK7 (left), and NIK7d (right) and bottom row for JHID7 (left) and SA8 (right) for the roots of the polynomial$ z^3-z $ . -
Figure 7. The top row for Newton. Second row for Halley (left) and BSC (right). Third row for Super Halley (left) and Ostrowski (right). Fourth row for Kung-Traub fourth order (left), JHIF4 (center) and CLND (right). Bottom row for KB74 (left) and Murakami (right) for the roots of the polynomial
$ z^4-10z^2+9 $ . -
Figure 8. The top row for Neta sixth order with
$ \beta = -1/2 $ (left) and N6d (right). Second row for CN6 (left) and WL6 (right). Third row for NIK7 (left), and NIK7d (right) and bottom row for JHID7 (left) and SA8 (right) for the roots of the polynomial$ z^4-10z^2+9 $ . -
Figure 9. The top row for Newton. Second row for Halley (left) and BSC (right). Third row for Super Halley (left) and Ostrowski (right). Fourth row for Kung-Traub fourth order (left), JHIF4 (center) and CLND (right). Bottom row for KB74 (left) and Murakami (right) for the roots of the polynomial
$ z^5-1 $ . -
Figure 10. The top row for N6d. Second row for CN6 (left) and WL6 (right). Third row for NIK7 (left), and NIK7d (right) and bottom row for JHID7 (left) and SA8 (right) for the roots of the polynomial
$ z^5-1 $ . -
Figure 11. The top row for Newton (left) Halley (center) and BSC (right). Second row for Super Halley (left) and Ostrowski (center) and Kung-Traub fourth order (right). Third row for JHIF4 (left), CLND (center) and KB74 (right). Fourth row for Murakami (left), CN6 (center) and WL6 (right). Fifth row for NIK7 (left), NIK7d (center) and JHID7 (right) and bottom row for SA8 for the roots of the polynomial
$ z^6-\frac 12 z^5 +\frac{11(i+1)}{4} z^4-\frac{3i+19}{4}z^3 +\frac{5i+11}{4} z^2 -\frac{i+11}{4}z+\frac 32-3i $ . -
Figure 12. The top row for Newton (left), Halley (center) and BSC (right). The second row for Super Halley(left), Ostrowski (center) and KT4 (right). The third row for JHIF4 (left), CLND (center) and KB74 (right). The fourth row for Murakami (left), CN6 (center) and WL6 (right). The fifth row for NIK7 (left), NIK7d (center) and JHID7 (right). The bottom row for SA8 for the roots of the function
$ (e^{z+1}-1)(z-1) $ .