| Citation: |
Lijuan Shi, Zhenshu Wen. SEVERAL TYPES OF PERIODIC WAVE SOLUTIONS AND THEIR RELATIONS OF A FUJIMOTO-WATANABE EQUATION[J]. Journal of Applied Analysis & Computation, 2019, 9(4): 1193-1203. doi: 10.11948/2156-907X.20180084
|
SEVERAL TYPES OF PERIODIC WAVE SOLUTIONS AND THEIR RELATIONS OF A FUJIMOTO-WATANABE EQUATION
-
Abstract
In this paper, we study periodic wave solutions of a Fujimoto–Watanabe equation by exploiting the bifurcation method of dynamical systems. We obtain all possible bifurcations of phase portraits of the system in different regions of the parametric space, and then give the sufficient conditions to guarantee the existence of several types of periodic wave solutions. What's more, we present their exact expressions and reveal their inside relations as well as their relations with solitary wave solutions.
-
-
References
[1] A. Biswas and M. Song, Soliton solution and bifurcation analysis of the Zakharov-Kuznetsov-Benjamin-Bona-Mahoney equation with power law nonlinearity, Commun. Nonlinear Sci. Numer. Simul., 2013, 18(7), 1676-1683. doi: 10.1016/j.cnsns.2012.11.014 [2] A. Biswas, M. Song, H. Triki et al., Solitons, shock waves, conservation laws and bifurcation analysis of Boussinesq equation with power law nonlinearity and dual dispersion, Appl. Math. Inform. Sci., 2014, 8(3), 949-957. doi: 10.12785/amis/080303 [3] A. Chen, S. Wen, S. Tang et al., Effects of quadratic singular curves in integrable equations, Studies in Applied Mathematics, 2015, 134(1), 24-61. doi: 10.1111/sapm.12060 [4] Y. Chen, M. Song and Z. Liu, Soliton and Riemann theta function quasiperiodic wave solutions for a (2+1)-dimensional generalized shallow water wave equation, Nonlinear Dyn, 2015, 82(1-2), 333-347. doi: 10.1007/s11071-015-2161-7 [5] X. Du, An irrational trial equation method and its applications, Journal of Physics, 2010, 75(3), 415-422. [6] A. Fujimoto and Y. Watanabe, Polynomial evolution equations of not normal type admitting nontrivial symmetries, Physics Letters A, 1989, 136(6), 294-299. doi: 10.1016/0375-9601(89)90820-7 [7] T. D. Leta and J. Li, Various exact soliton solutions and bifurcations of a generalized Dullin-Gottwald-Holm Equation with a power law nonlinearity, International Journal of Bifurcation and Chaos, 2017, 27(8), 1750129. doi: 10.1142/S0218127417501292 [8] J. Li, Singular Nonlinear Travelling Wave Equations: Bifurcations and Exact Solutions, Science Press, Beijing, 2013. [9] J. Li and Z. Qiao, Bifurcations and exact traveling wave solutions of the generalized two-component Camassa-Holm equation, Int. J. Bifurcat. Chaos., 2012, 22(12), 1250305. doi: 10.1142/S0218127412503051 [10] C. Liu, Applications of complete discrimination system for polynomial for classifications of traveling wave solutions to nonlinear differential equations, Computer Physics Communications, 2010, 181(2), 317-324. doi: 10.1016/j.cpc.2009.10.006 [11] Z. Liu and Y. Liang, The explicit nonlinear wave solutions and their bifurcations of the generalized Camassa-Holm equation, Int. J. Bifurcat. Chaos., 2011, 21(11), 3119-3136. doi: 10.1142/S0218127411030556 [12] C. Pan, L. Ling and Z. Liu, A new integrable equation with cuspons and periodic cuspons, Physica Scripta, 2014, 89(10), 105207. doi: 10.1088/0031-8949/89/10/105207 [13] S. Sakovich, Fujimoto-Watanabe equations and differential substitutions, Journal of Physics A: Mathematical and General, 1991, 24(10), L519-L521. doi: 10.1088/0305-4470/24/10/004 [14] S. Sergei, Smooth soliton solutions of a new integrable equation by Qiao, Journal of Mathematical Physics, 2011, 52(2), 023509. doi: 10.1063/1.3548837 [15] L. Shi and Z. Wen, Bifurcations and dynamics of traveling wave solutions to a Fujimoto-Watanabe equation, Commun. Theor. Phys., 2018, 69(6), 631-636. doi: 10.1088/0253-6102/69/6/631 [16] L. Shi and Z. Wen, Dynamics of traveling wave solutions to a highly nonlinear Fujimoto-Watanabe equation, Chinese Physics B, 2019, 28(4), 040201. doi: 10.1088/1674-1056/28/4/040201 [17] M. Song, Nonlinear wave solutions and their relations for the modified Benjamin-Bona-Mahony equation, Nonlinear Dyn, 2015, 80(1-2), 431-446. doi: 10.1007/s11071-014-1880-5 [18] Z. Wen, Bifurcation of solitons, peakons, and periodic cusp waves for θ- equation, Nonlinear Dyn, 2014, 77(1-2), 247-253. doi: 10.1007/s11071-014-1289-1 [19] Z. Wen, Several new types of bounded wave solutions for the generalized twocomponent Camassa-Holm equation, Nonlinear Dyn, 2014, 77(3), 849-857. doi: 10.1007/s11071-014-1346-9 [20] Z. Wen, Bifurcations and nonlinear wave solutions for the generalized twocomponent integrable Dullin-Gottwald-Holm system, Nonlinear Dyn, 2015, 82(1-2), 767-781. doi: 10.1007/s11071-015-2195-x [21] Z. Wen, Extension on peakons and periodic cusp waves for the generalization of the Camassa-Holm equation, Math Meth Appl Sci, 2015, 38(11), 2363-2375. doi: 10.1002/mma.v38.11 [22] Z. Wen, Bifurcations and exact traveling wave solutions of a new twocomponent system, Nonlinear Dynamics, 2017, 87(3), 1917-1922. doi: 10.1007/s11071-016-3162-x [23] Z. Wen, Bifurcations and exact traveling wave solutions of the celebrated GreenNaghdi equations, International Journal of Bifurcation and Chaos, 2017, 27(07), 1750114. doi: 10.1142/S0218127417501140 [24] Z. Wen and Z. Liu, Bifurcation of peakons and periodic cusp waves for the generalization of the Camassa-Holm equation, Nonlinear Anal., 2011, 12(3), 1698-1707. doi: 10.1016/j.nonrwa.2010.11.002 [25] Z. Wen, Z. Liu and M. Song, New exact solutions for the classical Drinfel'dSokolov-Wilson equation, Appl. Math. Comput., 2009, 215(6), 2349-2358. [26] Z. Wen and L. Shi, Dynamical behaviors of traveling wave solutions to a Fujimoto-Watanabe equation, Chinese Physics B, 2018, 27(9), 090201. doi: 10.1088/1674-1056/27/9/090201 [27] Z. Wen and L. Shi, Dynamics of bounded traveling wave solutions for the modified Novikov equation, Dynam. Syst. Appl., 2018, 27(3), 581-591. [28] L. Zhang, L. Chen and X. Huo, The effects of horizontal singular straight line in a generalized nonlinear Klein-Gordon model equation, Nonlinear Dyn, 2013, 72(4), 789-801. doi: 10.1007/s11071-013-0753-7 -
-
Figures(7)
Export File
Citation
Lijuan Shi, Zhenshu Wen. SEVERAL TYPES OF PERIODIC WAVE SOLUTIONS AND THEIR RELATIONS OF A FUJIMOTO-WATANABE EQUATION[J]. Journal of Applied Analysis & Computation, 2019, 9(4): 1193-1203. doi: 10.11948/2156-907X.20180084
Format
Content
DownLoad:
-
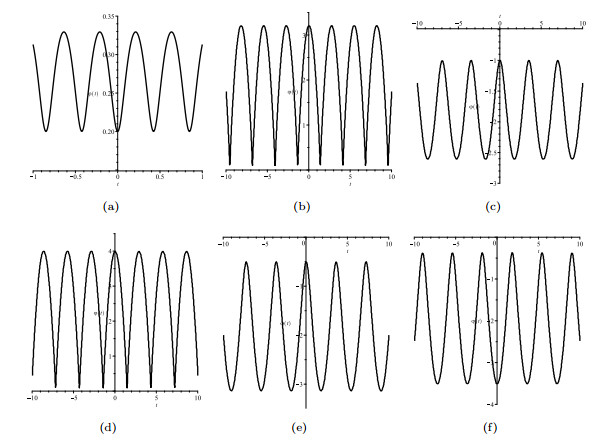
Figure 1. The graphics of the function
$ f(\varphi) $ -
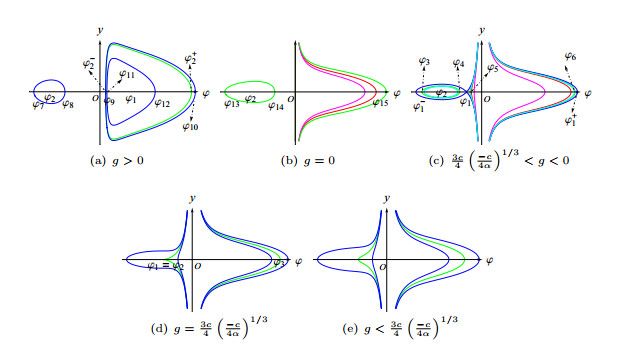
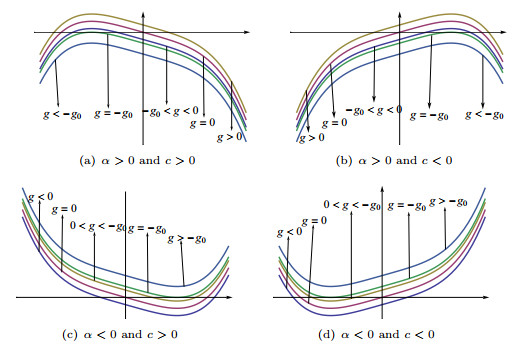
Figure 2. The phase portraits of system (2.3) when
$ \alpha>0 $ and$ c>0 $ -
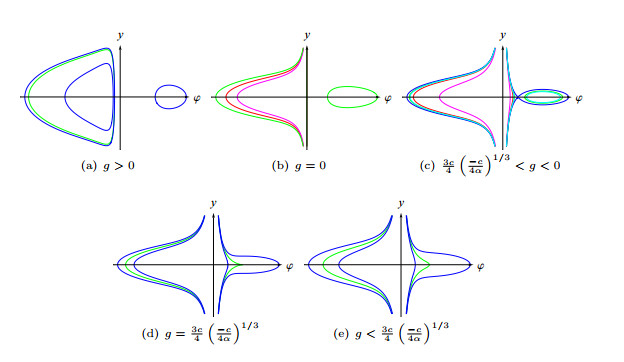
Figure 3. The phase portraits of system (2.3) when
$ \alpha>0 $ and$ c<0 $ -
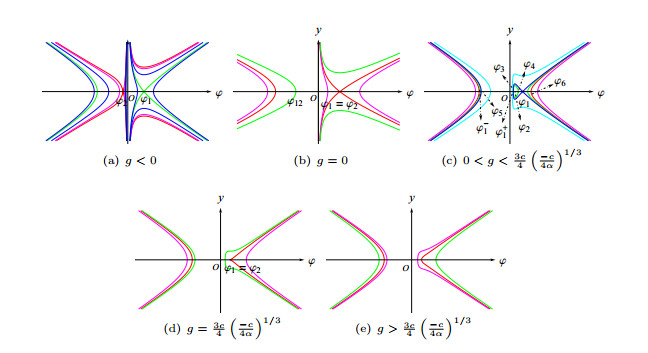
Figure 4. The phase portraits of system (2.3) when
$ \alpha<0 $ and$ c>0 $ -
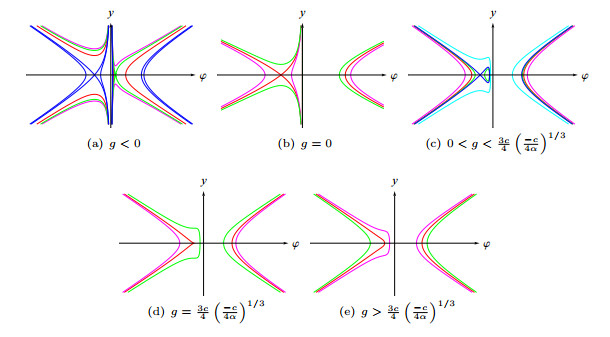
Figure 5. The phase portraits of system (2.3) when
$ \alpha<0 $ and$ c<0 $ - Figure 6. The profiles of periodic wave solutions (3.1), (3.2), (3.3), (3.4), (3.6), and (3.7), respectively
- Figure 7. The process of periodic wave solutions (3.22) converging to solitary wave solution (3.21)