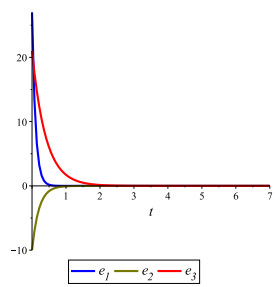
|
[1]
|
H. N. Agiza, On the analysis of stability, bifurcation, chaos and chaos control of kopel map, Chaos, Solitons & Fractals, 1999, 10(11), 1909-1916.
Google Scholar
|
|
[2]
|
S. K. Agrawal and S. Das, Function projective synchronization between four dimensional chaotic systems with uncertain parameters using modified adaptive control method, J. Process Control, 2014, 24(5), 517-530. doi: 10.1016/j.jprocont.2014.02.013
CrossRef Google Scholar
|
|
[3]
|
E. Bai and K. Lonngren, Sequential synchronization of two Lorenz system using active control, Chaos, Solitons & Fractals, 2000, 11(7), 1041-1044.
Google Scholar
|
|
[4]
|
N. Cai, Y. Jing and S. Zhang, Modified projective synchronization of chaotic systems with disturbances via active sliding mode control, Commun. Nonlinear Sci. Numer. Simul., 2010, 15(6), 1613-1620. doi: 10.1016/j.cnsns.2009.06.012
CrossRef Google Scholar
|
|
[5]
|
T. L. Carroll and L. M. Perora, Synchronizing chaotic circuits, IEEE Transactions on Circuits and Systems, 1991, 38(4), 453-456. doi: 10.1109/31.75404
CrossRef Google Scholar
|
|
[6]
|
G. Chen, Chaos on some controllability conditions for chaotic dynamics control, Chaos, Solitons & Fractals, 1997, 8(9), 1461-1470.
Google Scholar
|
|
[7]
|
Y. Chen and X. Li, Function projective synchronization between two identical chaotic systems, Int. J. Mod. Phys. C, 2007, 18(5), 883-888. doi: 10.1142/S0129183107010607
CrossRef Google Scholar
|
|
[8]
|
S. Dadras and H. Momeni, Control of a fractional-order economical system via sliding mode, Physica A, 2010, 389(12), 2434-2442. doi: 10.1016/j.physa.2010.02.025
CrossRef Google Scholar
|
|
[9]
|
H. Du, Q. Zeng and C. Wang, Function projective synchronization of different chaotic systems with uncertain parameters, Phys. Lett. A, 2008, 372(33), 5402-5410. doi: 10.1016/j.physleta.2008.06.036
CrossRef Google Scholar
|
|
[10]
|
E. M. Elabbasy, H. N. Agiza and M. M. El-Dessoky, Global chaos synchronization for four-scroll attractor by nonlinear control, Sci. Res. Essays, 2006, 1(3), 65-71.
Google Scholar
|
|
[11]
|
E. M. Elabbasy and M. M. El-Dessoky, Adaptive coupled synchronization of coupled chaotic dynamical systems, Trends Applied Sci. Res., 2007, 2(2), 88-102. doi: 10.3923/tasr.2007.88.102
CrossRef Google Scholar
|
|
[12]
|
E. M. Elabbasy and M. M. El-Dessoky, Synchronization of Van Der Pol oscillator and chen chaotic dynamical system, Chaos, Solitons & Fractals, 2008, 36(5), 1425-1435.
Google Scholar
|
|
[13]
|
M. M. El-Dessoky, Synchronization and anti-synchronization of a hyperchaotic Chen system, Chaos, Solitons & Fractals, 2009, 39(4), 1790-1797.
Google Scholar
|
|
[14]
|
M. M. El-Dessoky, Anti-synchronization of four scroll attractor with fully unknown parameters, Nonlinear Anal.-Real World Appl., 2010, 11(2), 778-783. doi: 10.1016/j.nonrwa.2009.01.048
CrossRef Google Scholar
|
|
[15]
|
M. M. El-Dessoky, E. O. Alzahrany, and N. A. Almohammadi. Function Projective Synchronization for Four Scroll Attractor by Nonlinear Control, Appl. Math. Sci., 2017, 11(26), 1247-1259.
Google Scholar
|
|
[16]
|
M. M. El-Dessoky and M. T. Yassen, Adaptive feedback control for chaos control and synchronization for new chaotic dynamical system, Math. Probl. Eng., 2012, Vol. 2012, Article ID 347210, 12 pages.
Google Scholar
|
|
[17]
|
A. Hegazi, H. N. Agiza and M. M. El-Dessoky, Controlling chaotic behaviour for spin generator and Rossler dynamical systems with feedback control, Chaos, Solitons & Fractals, 2001, 12(4), 631-658.
Google Scholar
|
|
[18]
|
J. Huang, Adaptive synchronization between different hyperchaotic systems with fully uncertain parameters, Phys. Lett. A, 2008, 372(27-28), 4799-4804. doi: 10.1016/j.physleta.2008.05.025
CrossRef Google Scholar
|
|
[19]
|
C. Hwang, J. Yuan, J. Hsieh and R. Lin, A linear continuous feedback control of chua's circuit, Chaos, Solitons & Fractals, 1997, 8(9), 1507-1515.
Google Scholar
|
|
[20]
|
G. Li, Modified projective synchronization of chaotic system, Chaos, Solitons & Fractals, 2007, 32(5), 1786-1790.
Google Scholar
|
|
[21]
|
G. Li, Generalized synchronization of chaos based on suitable separation, Chaos, Solitons & Fractals, 2009, 39(5), 2056-2062.
Google Scholar
|
|
[22]
|
C. Liu, T. Liu, L. Liu, and K. Liu, A new chaotic attractor, Chaos, Solitons & Fractals, 2004, 22(5), 1031-1038.
Google Scholar
|
|
[23]
|
A. Loria, Master-slave synchronization of fourth order Lu chaotic oscillators via linear output feadback, IEEE Trans. Circuits Syst. Ⅱ-Express Briefs, 2010, 57(3), 213-217. doi: 10.1109/TCSII.2010.2040303
CrossRef Google Scholar
|
|
[24]
|
K. Ojo, S. Ogunjo and A. Olagundoye, Projective synchronization via active control of identical chaotic oscillators with parametric and external excitation, International Journal of Nonlinear Science, 2017, 24(2), 76-83.
Google Scholar
|
|
[25]
|
E. Ott, C. Grebogi and J. Yorke, Controlling chaos, Phys. Rev. Lett., 1999, 64(11), 1179-1184.
Google Scholar
|
|
[26]
|
J. Park, Adaptive modified projective synchronization of a unified chaotic system with an uncertain parameter, Chaos, Solitons & Fractals, 2007, 34(5), 1552-1559.
Google Scholar
|
|
[27]
|
L. M. Pecora and T. L. Carroll, Synchronization in chaotic systems, Phys. Rev. Lett., 1990, 64(8), 821-824. doi: 10.1103/PhysRevLett.64.821
CrossRef Google Scholar
|
|
[28]
|
J. Petereit and A. Pikovsky, Chaos synchronization by nonlinear coupling, Commun. Nonlinear Sci. Numer. Simul., 2017, 44(C), 344-351.
Google Scholar
|
|
[29]
|
N. Rulkov, M. Sushchik, L. Tsimring and H. Abarbanel, Generalized synchronization of chaos in directionally coupled chaotic systems, Phys. Rev. Lett., 1995, 51(2), 980-994.
Google Scholar
|
|
[30]
|
L. Runzi and W. Zhengmin, Adaptive function projective synchronization of unified chaotic systems with uncertain parameters, Chaos, Solitons & Fractals, 2009, 42(2), 1266-1272.
Google Scholar
|
|
[31]
|
A. Singh and S. Gakkhar, Controlling chaos in a food chain model, Math. Comput. Simul., 2015, 115(C), 24-36.
Google Scholar
|
|
[32]
|
Y. Tang and J. Fang, General method for modified projective synchronization of hyperchaotic systems with known or unknown parameter, Phys. Lett. A, 2008, 372(11), 1816-1826. doi: 10.1016/j.physleta.2007.10.043
CrossRef Google Scholar
|
|
[33]
|
K. Vishal and S. Agrawal, On the dynamics, existence of chaos, control and synchronization of a novel complex chaotic system, Chin. J. Phys., 2017, 55(2), 519-532. doi: 10.1016/j.cjph.2016.11.012
CrossRef Google Scholar
|
|
[34]
|
X. Xu, Generalized function projective synchronization of chaotic systems for secure communication, EURASIP J. Adv. Signal Process., 2011, 2011(1), 6180-6187.
Google Scholar
|
|
[35]
|
C.-H. Yang and C.-L. Wu, Nonlinear dynamic analysis and synchronization of four-dimensional Lorenz-Stenflo system and its circuit experimental implementation, Abstract Appl. Anal., 2014, Vol. 2014, Article ID 213694, 17 pages.
Google Scholar
|
|
[36]
|
S. Yang and C. Duan, Generalized synchronization in chaotic systems, Chaos, Solitons & Fractals, 1998, 9(10), 1703-1707.
Google Scholar
|
|
[37]
|
X. Yang, A framework for synchronization theory Chaos, Solitons & Fractals, 2000, 11(9), 1365-1368.
Google Scholar
|
|
[38]
|
Y. Yua and H. Li, Adaptive generalized function projective synchronization of uncertain chaotic systems, Nonlinear Anal.-Real World Appl., 2010, 11(4), 2456-2464. doi: 10.1016/j.nonrwa.2009.08.002
CrossRef Google Scholar
|
|
[39]
|
S. Zheng, Adaptive modified function projective synchronization of unknown chaotic systems with different order, Appl. Math. Comput., 2011, 218(10), 5891-5899.
Google Scholar
|
|
[40]
|
S. Zheng, G. Dong and Q. Bi, Adaptive modified function projective synchronization of hyperchaotic systems with unknown parameters, Commun. Nonlinear Sci. Numer. Simul., 2010, 15(11), 3547-3556. doi: 10.1016/j.cnsns.2009.12.010
CrossRef Google Scholar
|




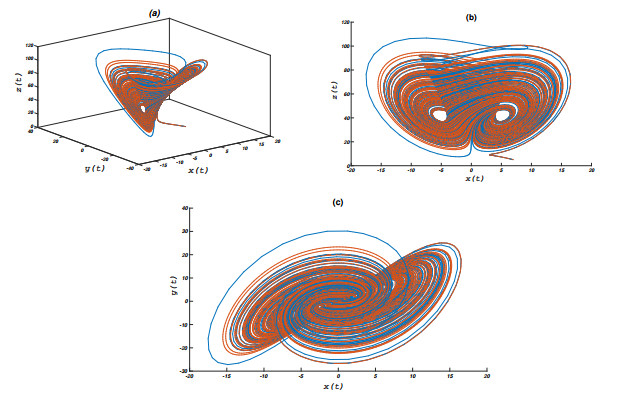

 DownLoad:
DownLoad: