| Citation: |
Jingli Ren, Ying Xu. A MICROBIAL CONTINUOUS CULTURE SYSTEM WITH DIFFUSION AND DIVERSIFIED GROWTH[J]. Journal of Applied Analysis & Computation, 2019, 9(3): 981-1006. doi: 10.11948/2156-907X.20180195
|
A MICROBIAL CONTINUOUS CULTURE SYSTEM WITH DIFFUSION AND DIVERSIFIED GROWTH
-
Abstract
A reaction-diffusion model is presented to describe the microbial continuous culture with diversified growth. The existence of nonnegative solutions and attractors for the system is obtained, the stability of steady states and the steady state bifurcation are studied under three growth conditions. In the case of no growth inhibition or only product inhibition, the system admits one positive constant steady state which is stable; in the case of growth inhibition only by substrate, the system can have two positive constant steady states, explicit conditions of the stability and the steady state bifurcation are also determined. In addition, numerical simulations are given to exhibit the theoretical results.-
Keywords:
- Continuous culture /
- diffusion /
- diversified growth /
- stability /
- steady state bifurcation
-
-
References
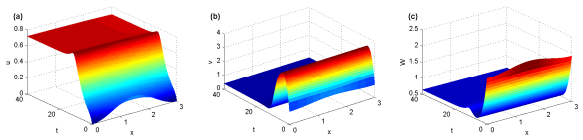
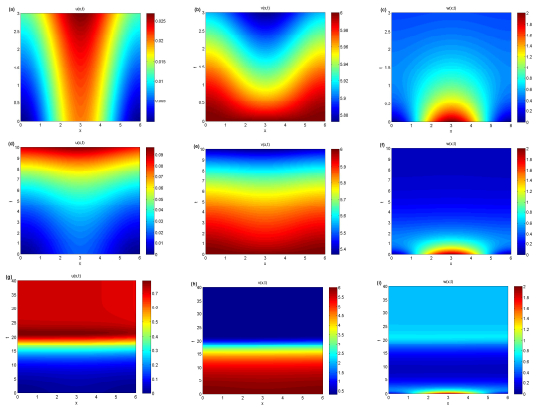
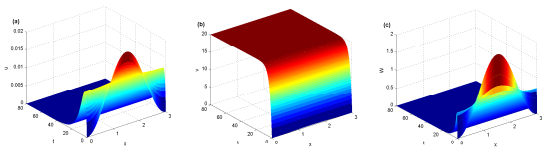
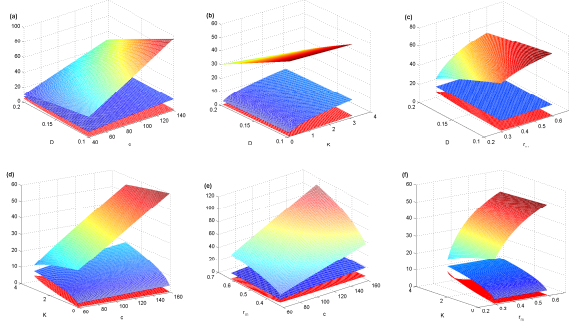
[1] K. J. Appeldoorn, A. J. Boom, G. J. J. Kortstee, A. J. B. Zehnder, Contribution of precipitated phosphates and acid-soluble polyphosphate to enhanced biological phosphate removal, Water Res., 1992, 26(7), 937–943. [2] J. F. Andrews, A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates, Biotechnol. Bioeng., 1968, 10(6), 707–723. [3] F. W. Bai, L. J. Chen, W. A. Anderson, M. Moo-Young, Parameter oscillations in a very high gravity medium continuous ethanol fermentation and their attenuation on a multistage packed column bioreactor system, Biotechnol. Bioeng., 2004, 88(5), 558–566. [4] M. Balat, Production of bioethanol from lignocellulosic materials via the biochemical pathway: A review, Energ. Convers. Manage., 2011, 52(2), 858–875. [5] H. Biebl, Glycerol fermentation of 1, 3-propanediol by Clostridium butyricum. Measurement of product inhibition by use of a pH-auxostat, Appl. Microbiol. Biot., 1991, 35(6), 701–705. [6] E. A. Buehler, A. Mesbah, Kinetic study of Acetone-Butanol-Ethanol fermentation in continuous culture, Plos One, 2016, 11(8), 1932–6203. [7] A. Carruthers, Mechanisms for the facilitated diffusion of substrates across cell membranes, Biochemistry, 1991, 30(16), 3898–3906. [8] D. E. Contois, Kinetics of bacterial growth: relationship between population density and specific growth rate of continuous cultures, J. Gen. Microbiol., 1959, 21(1), 40–50. [9] E. N. Dancer, Y. H. Du, Positive solutions for a three-species competition system with diffusion-I. General existence results, Nonlinear Anal., 1995, 24(3), 337–357. [10] V. H. Edwards, R. C. Ko, S. A. Balogh, Dynamics and control of continuous microbial propagators to subject substrate inhibition, Biotechnol. Bioeng., 1972, 14(6), 939–974. [11] M. Esfandyari, M. A. Fanaei, R. Gheshlaghi, M. A. Mahdavi, Mathematical modeling of two-chamber batch microbial fuel cell with pure culture of Shewanella, Chem. Eng. Res. Des., 2017,117, 34–42. [12] C. X. Gao, E. M. Feng, Z. T. Wang, Z. L. Xiu, Parameters identification problem of the nonlinear dynamical system in microbial continuous cultures, Appl. Math. Comput., 2005,169(1), 476–484. [13] D. Henry, Geometric Theory of Semilinear Parabolic Equations, Lecture Notes in Mathematics, Springer-Verlag, Berlin, 1981. [14] E. Krichen, J. Harmand, M. Torrijos, J. J. Godon, N. Bernet, A. Rapaport, High biomass density promotes density-dependent microbial growth rate, Biochem. Eng. J., 2018,130, 66–75. [15] O. Levenspiel, The Monod equation: A revisit and a generalization to product inhibition situations, Biotechnol, Bioeng., 1980, 22(8), 1671–1687. [16] J. H. T. Luong, Kinetics of ethanol inhibition in alcohol fermentation, Biotechnol. Bioeng., 1985, 27(3), 280–285. [17] C. V. Pao, Nonlinear Parabolic and Elliptic Equations, Springer Science & Business Media, New York, 1992. [18] C. V. Pao, Quasisolutions and global attactor of reaction-diffusion systems, Nonlinear Anal., 1996, 26(12), 1889–1903. [19] J. L. Ren and Q. G. Yuan, Bifurcations of a periodically forced microbial continuous culture model with restrained growth rate, Chaos, 2017, 27(8), 083124. [20] Y. Shen, X. Q. Zhao, X. M. Ge, F. W. Bai, Metabolic flux and cell cycle analysis indicating new mechanism underlying process oscillation in continuous ethanol fermentation with Saccharomyces cerevisiae under VHG conditions, Biotechnol. Adv., 2009, 27(6), 1118–1123. [21] P. Skupin, M. Metzger, Stability analysis of the continuous ethanol fermentation process with a delayed product inhibition, Appl. Math. Model., 2017, 49, 48–58. [22] Z. L. Xiu, A. P. Zeng, W. D. Deckwer, Multiplicity and stability analysis of microorganisms in continuous culture: effects of metabolic overflow and growth inhibition, Biotechnol. Bioeng., 1998, 57(3), 251–261. [23] T. Yano, S. Koga, Dynamic behavior of the chemostat subject to substrate inhibition, Biotechnol. Bioeng., 1969, 11(2), 139–153. [24] J. X. Ye, E. M. Feng, H. S. Lian, Z. L. Xiu, Existence of equilibrium points and stability of the nonlinear dynamical system in microbial continuous cultures, Appl. Math. Comput., 2009,207(2), 307–318. [25] F. Yi, J. Wei, J. Shi, Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator–prey system, J. Differ. Equations, 2009,246(5), 1944–1977. [26] A. P. Zeng, A. Ross, H. Biebl, C. Tag, B. Gunzel, W. D. Deckwer, Multiple product inhibition and growth modeling of clostridium butyricum and klebsiella pneumoniae in glycerol fermentation, Biotechnol. Bioeng., 1994, 44(8), 902–911. -
-
Figures(5)
Export File
Citation
Jingli Ren, Ying Xu. A MICROBIAL CONTINUOUS CULTURE SYSTEM WITH DIFFUSION AND DIVERSIFIED GROWTH[J]. Journal of Applied Analysis & Computation, 2019, 9(3): 981-1006. doi: 10.11948/2156-907X.20180195
Format
Content
DownLoad:
-
Figure 1. The asymptotic behaviors of
$ u(x, t) $ in$ (a) $ ,$ v(x, t) $ in$ (b) $ and$ w(x, t) $ in$ (c) $ . Here$ r_m = 0.01 $ ,$ D = 0.55 $ ,$ a_0 = 6 $ ,$ d_1 = 0.3 $ ,$ d_2 = 1.1 $ ,$ d_3 = 1 $ ,$ n_s = 1 $ ,$ Y_s = 0.4 $ ,$ K = 0.28 $ ,$ n_p = 0.8 $ ,$ Y_p = 50 $ ; initial function (5.1) is chosen. -
Figure 2. The asymptotic behaviors of
$ u(x, t) $ in$ (a) $ ,$ v(x, t) $ in$ (b) $ and$ w(x, t) $ in$ (c) $ . Here$ r_m = 0.6 $ ,$ D = 0.35 $ ,$ a_0 = 6 $ ,$ d_1 = 0.3 $ ,$ d_2 = 1.1 $ ,$ d_3 = 1.1 $ ,$ n_s = 1 $ ,$ Y_s = 0.2 $ ,$ r_m = 0.6 $ ,$ K = 0.28 $ ,$ n_p = 0.05 $ ,$ Y_p = 0.8 $ ; initial function (5.1) is used. -
Figure 3. The spatiotemporal patterns of
$ u(x, t) $ in$ (a, d, g) $ ,$ v(x, t) $ in$ (b, e, h) $ and$ w(x, t) $ in$ (c, f, i) $ . Here,$ L = 6 $ , all the other parameters take the same values as them in Figure 2; initial function (5.2) is used. -
Figure 4. The asymptotic behaviors of
$ u(x, t) $ in$ (a) $ ,$ v(x, t) $ in$ (b) $ and$ w(x, t) $ in$ (c) $ . Here$ a_0 = 20 $ ,$ c = 30 $ and all the other parameters take the same values as them in Figure 2; initial function (5.1) is chosen. -
Figure 5. The graphs of
$ v_1^* $ ,$ s $ and$ v_2^* $ with respect to parameters$ c $ and$ D $ in$ (a) $ ,$ K $ and$ D $ in$ (b) $ ,$ r_m $ and$ D $ in$ (c) $ ,$ c $ and$ K $ in$ (d) $ ,$ c $ and$ r_m $ in$ (e) $ ,$ r_m $ and$ K $ in$ (f) $ .