| Citation: |
Mingzhu Qu, Chunrui Zhang. TURING INSTABILITY AND PATTERNS OF THE FITZHUGH-NAGUMO MODEL IN SQUARE DOMAIN[J]. Journal of Applied Analysis & Computation, 2021, 11(3): 1371-1390. doi: 10.11948/20200182
|
TURING INSTABILITY AND PATTERNS OF THE FITZHUGH-NAGUMO MODEL IN SQUARE DOMAIN
-
Abstract
In this paper, critical conditions of Turing instability for Fitzhugh-Nagumo (FHN) model with diffusion under Neumann boundary conditions are derived. Moreover, different from previous works about the FHN model, we obtain simple bifurcation, double bifurcation, and four-fold bifurcation with stripe pattern, rectangular pattern, spot pattern, square pattern, and highly developed square pattern, respectively. Meanwhile, the theoretical results are applied to two coupled FHN model with diffusion, and the process of the coupling strengths affecting the stability of the model is presented by numerical simulations.
-
Keywords:
- Turing instability /
- coupled Fitzhugh-Nagumo /
- diffusion /
- pattern
-
-
References
[1] I. Biktasheva, A. Holden and V. Biktashev, Localization of response functions of spiral waves in the FitzHugh-Nagumo system, Int. J. Bifurcation Chaos, 2006, 16(5), 1547-1555. doi: 10.1142/S0218127406015490 [2] N. Buric and D. Todorovic, Dynamics of FitzHugh-Nagumo excitable systems with delayed coupling, Phys. Rev. E, 2003, 67(2), 066222. [3] S. Chowdhury, M. Biswas and R. Dutta, Approximate controllability of the FitzHugh-Nagumo equation in one dimension, J. Differ. Equ., 2020, 268(7), 3497-3563. doi: 10.1016/j.jde.2019.10.001 [4] B. Ermentrout, Stripes or spots? Nonlinear effects in bifurcation of reaction-diffusion equations on the square, Proc. R. Soc. A-Math. Phys. Eng. Sci., 1991, 434(1891), 413-417. [5] G. Ermentrout and J. Cowan, A mathematical theory of visual hallucination patterns, Biol. Cybern., 1979, 34(3), 137-150. doi: 10.1007/BF00336965 [6] P. Fife, Mathematical aspects of reacting and diffusing systems, Springer-Verlag, 1979. [7] R. Fitzhugh, Impulses and physiological states in theoretical models of nerve membrane, Biophys. J., 1961, 1(6), 445-466. doi: 10.1016/S0006-3495(61)86902-6 [8] D. Fan and L. Hong, Hopf bifurcation analysis in a synaptically coupled FHN neuron model with delays, Commun. Nonlinear Sci. Numer. Simul., 2010, 15(7), 1873-1886. doi: 10.1016/j.cnsns.2009.07.025 [9] P. Gong and J. Xu, Global dynamics and stochastic resonance of the forced FitzHugh-Nagumo neuron model, Phys. Rev. E, 2001, 63(3), 031906. doi: 10.1103/PhysRevE.63.031906 [10] V. Gaiko, Global bifurcations of multiple limit cycles in the FitzHugh-Nagumo system, Mathematics, 2011, 74(18), 7532-7542. [11] A. Hodgkin and A. Huxley, A quantitative description of membrane current and its application to conduction and excitation in nerve, J. Physiol. London, 1952, 117(4), 500-544. doi: 10.1113/jphysiol.1952.sp004764 [12] W. Jiang, H. Wang and X. Cao, Turing instability and Turing-Hopf bifurcation in diffusive Schnakenberg systems with gene expression time delay, J. Dyn. Differ. Equ., 2018, 31(4), 2223-2247. [13] A. Jalnine, Hyperbolic and non-hyperbolic chaos in a pair of coupled alternately excited FitzHugh-Nagumo systems. Commun. Nonlinear Sci. Numer. Simul., 2013, 23(1-3), 202-208. [14] G. Le, A. Pocheau and V. Croquette, Square versus roll pattern at convective threshold, Phys. Rev. Lett., 1985, 54(23), 2501-2504. doi: 10.1103/PhysRevLett.54.2501 [15] J. Li, H. Wang and Q. Ouyang, Square Turing patterns in reaction-diffusion systems with coupled layers, Chaos, 2014, 24(2), 023115. doi: 10.1063/1.4875262 [16] J. Murray, Mathematical biology, Biomath, 2002, 19(1-2), 261-283. [17] S. Mohyud-Din, Y. Khan, N. Faraz, et al., Exp-function method for solitary and periodic solutions of Fitzhugh-Nagumo equation, Int. J. Numer. Methods Heat Fluid Flow, 2012, 22(3), 335-341. doi: 10.1108/09615531211208042 [18] Y. Nishiura, Global structure of bifurcating solutions of some reaction-diffusion system, SIAM Journal on Mathematical Analysis, 1982, 13(4), 555-593. doi: 10.1137/0513037 [19] J. Nagumo, S. Arimoto and S. Yoshizawa, An active pulse transmission line simulating nerve axon, Proceedings of the Ire, 1962, 50(10), 2061-2070. doi: 10.1109/JRPROC.1962.288235 [20] I. Nagy, V. Romanovski and J. Toth, Two nested limit cycles in two-species reactions, Mathematics, 2020, 8(10), 1658. doi: 10.3390/math8101658 [21] Q. Ouyang, Nonlinear science and pattern dynamics, Peking University Press, Beijing, 2010. [22] D. Olmos and B. Shizgal, Pseudospectral method of solution of the Fitzhugh-Nagumo equation, Math. Comput. Simul., 2009, 79(7), 2258-2278. doi: 10.1016/j.matcom.2009.01.001 [23] M. Pierre, T. Suzuki and H. Umakoshi, Asymptotic behavior in chemical reaction-diffusion systems with boundary equilibria, J. Appl. Anal. Comput., 2018, 8(3), 836-858. [24] R. Rameh, E. Cherry and R. Santos, Single-variable delay-differential equation approximations of the Fitzhugh-Nagumo and Hodgkin-Huxley models, Commun. Nonlinear Sci. Numer. Simul., 2020, 82, 105066. doi: 10.1016/j.cnsns.2019.105066 [25] B. Sounvoravong and S. Guo, N-dark soliton solutions for the multicomponen Maccari system, Journal of Nonlinear Modeling and Analysis, 2019, 1(3), 319-334. [26] Y. Song, H. Jiang and Y. Yuan, Turing-Hopf bifurcation in the reaction-diffusion system with delay and application to a diffusive predator-prey model, J. Appl. Anal. Comput., 2019, 9(3), 1132-1164. [27] Y. Song, S. Wu and H. Wang, Spatiotemporal dynamics in the single population model with memory-based diffusion and nonlocal effect, J. Differ. Equ., 2019, 267(11), 6316-6251. doi: 10.1016/j.jde.2019.06.025 [28] Y. Song and J. Xu, Inphase and antiphase synchronization in a delay-coupled system with applications to a delay-coupled FitzHugh-Nagumo system, IEEE Trans. Neural Netw. Learn. Syst., 2012, 23(10), 1659-1670. doi: 10.1109/TNNLS.2012.2209459 [29] A. Turing, The chemical basis of morphogenesis. Philosophical Transactions of The Royal Society, Series B, Biological Sciences, 1952, 237(641), 37-72. [30] C. Varea, J. Aragon and R. Barrio, Confined Turing patterns in growing systems, Phys. Rev. E, 1997, 56(1), 1250-1253. doi: 10.1103/PhysRevE.56.1250 [31] C. Wagner, H. Muller and K. Knorr, Pattern formation at the bicritical point of the Faraday instability, Phys. Rev. E, 2003, 68(6), 066204. doi: 10.1103/PhysRevE.68.066204 [32] C. Zhang, A. Ke and B. Zheng, Patterns of interaction of coupled reaction-diffusion systems of the FitzHugh-Nagumo type, Nonlinear Dyn., 2019, 97(2), 1451-1476. doi: 10.1007/s11071-019-05065-8 -
-
Figures(16) / Tables(1)
Export File
Citation
Mingzhu Qu, Chunrui Zhang. TURING INSTABILITY AND PATTERNS OF THE FITZHUGH-NAGUMO MODEL IN SQUARE DOMAIN[J]. Journal of Applied Analysis & Computation, 2021, 11(3): 1371-1390. doi: 10.11948/20200182
Format
Content
DownLoad:
-
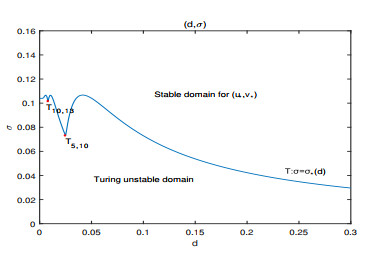
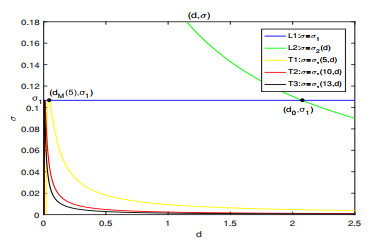
Figure 1. The figure of functions
$ \sigma = {\sigma _1} $ ,$ \sigma = {\sigma _2}\left( d \right) $ and$ \sigma = {\sigma _{\rm{*}}}\left( {k, d} \right) $ ,$ d > 0 $ ,$ k = 5, 10, 13 \cdots $ , in$ \left( {d, \sigma } \right) $ plane. -
Figure 2. The Turing bifurcation line
$ \mathrm{T} : \sigma = {\sigma _*}\left( d \right) $ ,$ d > 0 $ . -
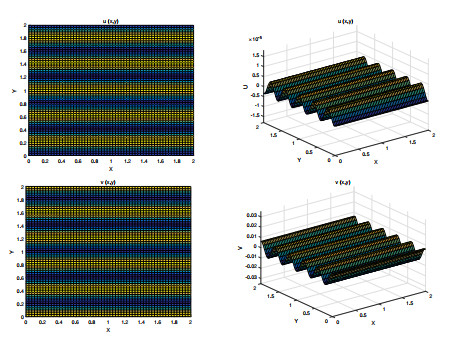
Figure 3. Stripe patterns when
$ {k_1} = 10 $ ,$ {m_1} = 10 $ ,$ {n_1} = 0 $ . The initial values are$ u0 = 0.00000002\cos \left( {5\pi x} \right) $ ,$ v0 = 0.007\cos \left( {5\pi y} \right) $ . -
Figure 4. Rectangular patterns when
$ {k_1} = 10 $ ,$ {m_3} = 8 $ ,$ {n_3} = 6 $ . The initial values are$ u0 = 0.00000002\cos \left( {4\pi x} \right)\cos \left( {3\pi y} \right) $ ,$ v0 = 0.007\cos \left( {3\pi x} \right)\cos \left( {4\pi y} \right) $ . -
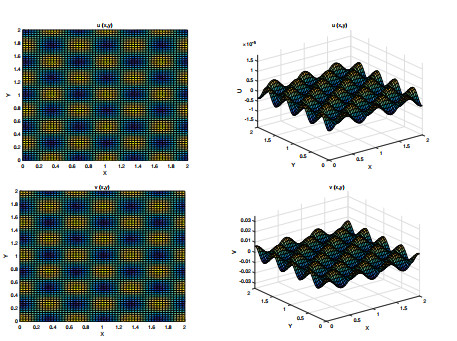
Figure 5. Spot patterns when
$ {k_1} = 10 $ ,$ {m_1} = 10 $ ,$ {n_1} = 0 $ ,$ {m_2} = 0 $ ,$ {n_2} = 10 $ by interacting$ {m_{1, 2}} $ ,$ {n_{1, 2}} $ two modes. The initial values are$ u0 = 0.002\cos \left( {5\pi x} \right) + 0.003\cos \left( {5\pi y} \right) $ ,$ v0 = 0.005\cos \left( {5\pi y} \right) - 0.004\cos \left( {5\pi x} \right) $ . -
Figure 6. Square patterns when
$ {k_1} = 10 $ ,$ {m_3} = 8 $ ,$ {n_3} = 6 $ ,$ {m_4} = 6 $ ,$ {n_4} = 8 $ by interacting$ {m_{3, 4}} $ ,$ {n_{3, 4}} $ two modes. The initial values are$ u0 = 0.007\cos \left( {4\pi x} \right)\cos \left( {3\pi y} \right) + 0.005\cos \left( {3\pi x} \right)\cos \left( {4\pi y} \right) $ ,$ v0 = 0.001\cos \left( {3\pi x} \right)\cos \left( {4\pi y} \right) - 0.002\cos \left( {4\pi x} \right)\cos \left( {3\pi y} \right) $ . -
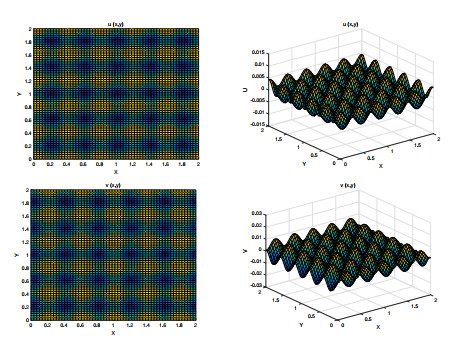
Figure 7. Highly developed square patterns when
$ {k_1} = 10 $ ,$ {m_1} = 10 $ ,$ {n_1} = 0 $ ,$ {m_2} = 0 $ ,$ {n_2} = 10 $ ,$ {m_3} = 8 $ ,$ {n_3} = 6 $ ,$ {m_4} = 6 $ ,$ {n_4} = 8 $ by interacting$ {m_{1, 2, 3, 4}} $ ,$ {n_{1, 2, 3, 4}} $ four modes. The initial values are$ u0 = 0.007\cos \left( {5\pi x} \right) + 0.005\cos \left( {5\pi y} \right) + 0.006\cos \left( {4\pi x} \right)\cos \left( {3\pi y} \right) + 0.009\cos \left( {3\pi x} \right)\cos \left( {4\pi y} \right) $ ,$ v0 = 0.007\cos \left( {5\pi y} \right) - 0.005\cos \left( {5\pi x} \right) + 0.006\cos \left( {3\pi x} \right)\cos \left( {4\pi y} \right) - 0.009\cos \left( {4\pi x} \right)\cos \left( {3\pi y} \right) $ . -
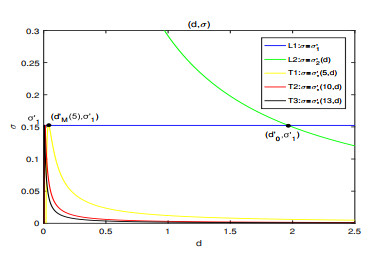
Figure 8. The figure of functions
$ \sigma = {\sigma _1^{'}} $ ,$ \sigma = {\sigma _2^{'}}\left( d \right) $ and$ {\sigma _{\rm{*}}^{'}}\left( {k, d} \right) $ ,$ d > 0 $ ,$ k = 5, 10, 13 \cdots $ , in$ \left( {d, \sigma } \right) $ plane. -
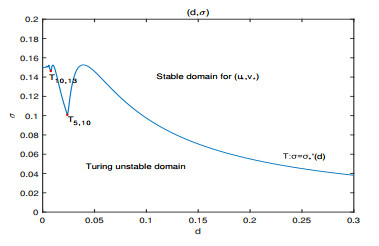
Figure 9. The Turing bifurcation line
$ \mathrm{T} : \sigma = {\sigma _*^{'}}\left( d \right) $ ,$ d > 0 $ . -
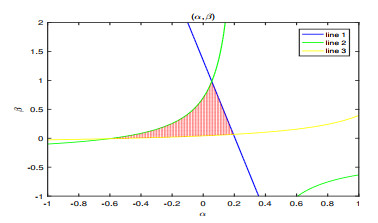
Figure 10. The region of coupling strengths
$ \alpha $ and$ \beta $ when$ d = 0.01 $ ,$ \sigma = 0.14 $ ,$ a = - 2.25 $ ,$ \delta = - 0.6 $ ,$ \varepsilon = 0.153 $ ,$ l = 2 $ . -
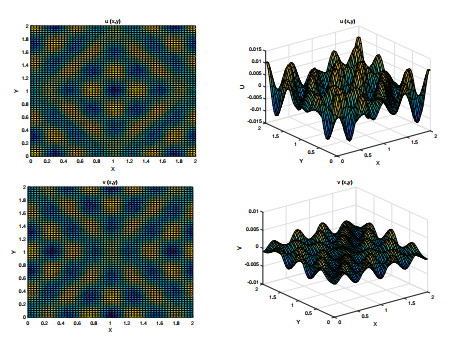
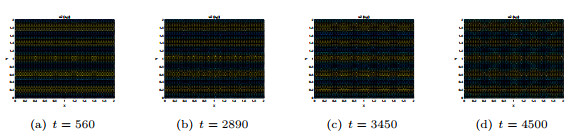
Figure 11. Stripe patterns produced by
$ {u_1}\left( {x, y} \right) $ when$ {m_1} = 10 $ ,$ {n_1} = 0 $ . -
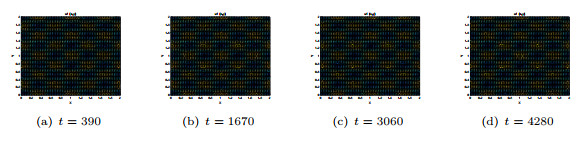
Figure 12. Spot patterns produced by
$ {u_2}\left( {x, y} \right) $ when$ {m_1} = 10 $ ,$ {n_1} = 0 $ . -
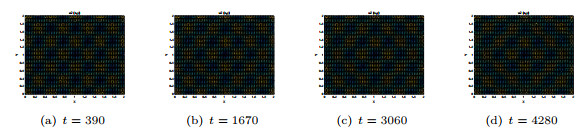
Figure 13. Spot patterns produced by
$ {v_2}\left( {x, y} \right) $ when$ {m_1} = 10 $ ,$ {n_1} = 0 $ . -
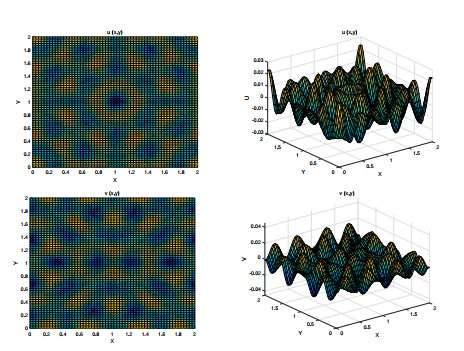
Figure 14. Rectangular patterns produced by
$ {u_1}\left( {x, y} \right) $ when$ {m_3} = 8 $ ,$ {n_3} = 6 $ . -
Figure 15. Square patterns produced by
$ {u_2}\left( {x, y} \right) $ when$ {m_3} = 8 $ ,$ {n_3} = 6 $ . -
Figure 16. Square patterns produced by
$ {v_2}\left( {x, y} \right) $ when$ {m_3} = 8 $ ,$ {n_3} = 6 $ .