| Citation: |
Fahd Karami, Dris Meskine, Khadija Sadik. A NEW NONLOCAL MODEL FOR THE RESTORATION OF TEXTURED IMAGES[J]. Journal of Applied Analysis & Computation, 2019, 9(6): 2070-2095. doi: 10.11948/20170189
|
A NEW NONLOCAL MODEL FOR THE RESTORATION OF TEXTURED IMAGES
-
Abstract
In this paper, we focus on the mathematical and numerical study of a new nonlocal reaction-diffusion system for image denoising. This model is motivated by involving the decomposition approach of $H^{-1}$ norm suggested by Meyer [25] which is more appropriate to represent the oscillatory patterns and small details in the textured image. Based on Schaeffer's fixed point theorem, we prove the existence and uniqueness of solution of the proposed model. To illustrate the efficiency and effectiveness of our model, we test the denoising experimental results as well we compare with some existing models in the literature. -
-
References
[1] L. Afraites, A. Atlas, F. Karami and D. Meskine, Some class of parabolic systems applied to image processing, Discrete Contin. Dyn. Syst. Ser. B, 2016, 21(6), 1671-1687. doi: 10.3934/dcdsb.2016017 [2] L. Alvarez, P.-L. Lions and J. M. Morel, Image selective smoothing and edge detection by nonlinear diffusion. II, SIAM J. Numer. Anal., 1992, 29(3), 845-866. doi: 10.1137/0729052 [3] F. Andreu, J. M. Mazón, J. D. Rossi and J. Toledo, A nonlocal p-Laplacian evolution equation with nonhomogeneous Dirichlet boundary conditions, SIAM J. Math. Anal., 2008/09, 40(5), 1815-1851. [4] F. Andreu, J. M. Mazón, J. D. Rossi and J. Toledo, Nonlocal diffusion problems, 165 of Mathematical Surveys and Monographs, American Mathematical Society, Providence, RI; Real Sociedad Matemática Española, Madrid, 2010. [5] A. Atlas, F. Karami and D. Meskine, The Perona-Malik inequality and application to image denoising, Nonlinear Anal. Real World Appl., 2014, 18, 57-68. doi: 10.1016/j.nonrwa.2013.11.006 [6] G. Aubert and P. Kornprobsty, New algorithm for solving variational problems in $w^{1, p}(\omega)$ and $bv(\omega)$: Application to image restoration, Research Report, RR-6245, INRIA, 2007, 25. [7] H. Brezis, New approximations of the total variation and filters in imaging, Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl., 2015, 26(2), 223-240. doi: 10.4171/RLM/704 [8] A. Buades, B. Coll and J. M. Morel, A review of image denoising algorithms, with a new one, Multiscale Model. Simul., 2005, 4(2), 490-530. doi: 10.1137/040616024 [9] S. G. Chang, B. Yu and M. Vetterli, Adaptive wavelet thresholding for image denoising and compression, IEEE Trans. Image Process., 2000, 9(9), 1532-1546. doi: 10.1109/83.862633 [10] K. Dabov, A. Foi, V. Katkovnik and K. Egiazarian, Image denoising by sparse 3-D transform-domain collaborative filtering, IEEE Trans. Image Process., 2007, 16(8), 2080-2095. doi: 10.1109/TIP.2007.901238 [11] M. Elad, On the origin of the bilateral filter and ways to improve it, IEEE Trans. Image Process., 2002, 11(10), 1141-1151. doi: 10.1109/TIP.2002.801126 [12] A. Elmoataz, D. Xavier and O. Lezoray, Non-local morphological pdes and p-laplacian equation on graphs with applications in image processing and machine learning, IEEE Journal of Selected Topics in Signal Processing, 2012, (6), 764-779. [13] G. Gilboa and S. Osher, Nonlocal linear image regularization and supervised segmentation, Multiscale Model. Simul., 2007, 6(2), 595-630. doi: 10.1137/060669358 [14] G. Gilboa and S. Osher, Nonlocal operators with applications to image processing, Multiscale Model. Simul., 2008, 7(3), 1005-1028. [15] Z. Guo, Q. Liu, J.Sun and B. Wu, Reaction-diffusion systems with p(x)-growth for image denoising, Nonlinear Anal. Real World Appl., 2011, 12(5), 2904-2918. doi: 10.1016/j.nonrwa.2011.04.015 [16] Z. Guo, J. Yin and Q. Liu, On a reaction-diffusion system applied to image decomposition and restoration, Math. Comput. Modelling, 2011, 53(5-6), 1336-1350. doi: 10.1016/j.mcm.2010.12.031 [17] Y. Jin, J. Jost and G. Wang, A new nonlocal variational setting for image processing, Inverse Probl. Imaging, 9(2), 415-430. doi: 10.3934/ipi.2015.9.415 [18] F. Karami, K. Sadik and L. Ziad, A variable exponent nonlocal $p(x)$-Laplacian equation for image restoration, Comput. Math. Appl., 2018, 75(2), 534-546. doi: 10.1016/j.camwa.2017.09.034 CrossRef $p(x)$-Laplacian equation for image restoration" target="_blank">Google Scholar
[19] S. Kindermann, S. Osher and P. Jones, Deblurring and denoising of images by nonlocal functionals, Multiscale Model. Simul., 2005, 4(4), 1091-1115. doi: 10.1137/050622249 [20] O. Kleinschmidt, T. Brox and D. Cremers, Nonlocal texture filtering with efficient tree structures and invariant patch similarity measures, Proc. International Workshop on Local and Non- local Approximation in Image Processing. Lausanne, Switzerland: IEEE SP/CAS Chapter in Finland, 2008, 103-113. [21] X. Liu and L. Huang, A new nonlocal total variation regularization algorithm for image denoising, Math. Comput. Simulation, 2014, 97, 224-233. doi: 10.1016/j.matcom.2013.10.001 [22] M. Maggioni, G. Boracchi, A. Foi and K. Egiazarian, Video denoising, deblocking and enhancement through separable 4-d nonlocal spatiotemporal transforms, IEEE Trans. Image Process., 2012, 21(9), 3952-3966. doi: 10.1109/TIP.2012.2199324 [23] M. Maggioni and A. Foi, Nonlocal transform-domain denoising of volumetric data with groupwise adaptive variance estimation, Proc. SPIE Electronic Imaging 2012, Computational Imaging X, 2012, 8296-22. [24] M. Maggioni, V. Katkovnik, K. Egiazarian and A. Foi, A nonlocal transform-domain filter for volumetric data denoising and reconstruction, IEEE Trans. Image Process., 2013, 22(2), 119-133. [25] Y. Meyer, Oscillating patterns in image processing and nonlinear evolution equations, 22 of University Lecture Series, American Mathematical Society, Providence, RI, 2001. The fifteenth Dean Jacqueline B. Lewis memorial lectures. [26] S. Osher, A. Solé and L. Vese, Image decomposition and restoration using total variation minimization and the $H^{-1}$ norm, Multiscale Model. Simul., 2003, 1(3), 349-370. doi: 10.1137/S1540345902416247 [27] P. Perona and J. Malik, Scale-space and edge detection using anisotropic diffusion, IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12, 629-639. doi: 10.1109/34.56205 [28] L. Rudin, S. Osher and E. Fatemi, Nonlinear total variation based noise removal algorithms, Phys. D, 1992, 60(1-4), 259-268. Experimental mathematics: computational issues in nonlinear science (Los Alamos, NM, 1991). [29] O. Seungmi, W. Hyenkyun, Y. Sangwoon and K. Myungjoo, Non-convex hybrid total variation for image denoising, J. Vis. Commun. Image R., 2013, 24, 332-344. doi: 10.1016/j.jvcir.2013.01.010 [30] J. Simon, Compact sets in the space $L^p(0,T;B)$, Ann. Mat. Pura Appl. (4), 1987, 146, 65-96. [31] L. P. Yaroslavsky, Digital picture processing, 9 of Springer Series in Information Sciences, Springer-Verlag, Berlin, 1985. An introduction. -
-
Figures(11) / Tables(4)
Export File
Citation
Fahd Karami, Dris Meskine, Khadija Sadik. A NEW NONLOCAL MODEL FOR THE RESTORATION OF TEXTURED IMAGES[J]. Journal of Applied Analysis & Computation, 2019, 9(6): 2070-2095. doi: 10.11948/20170189
Format
Content
DownLoad:
-
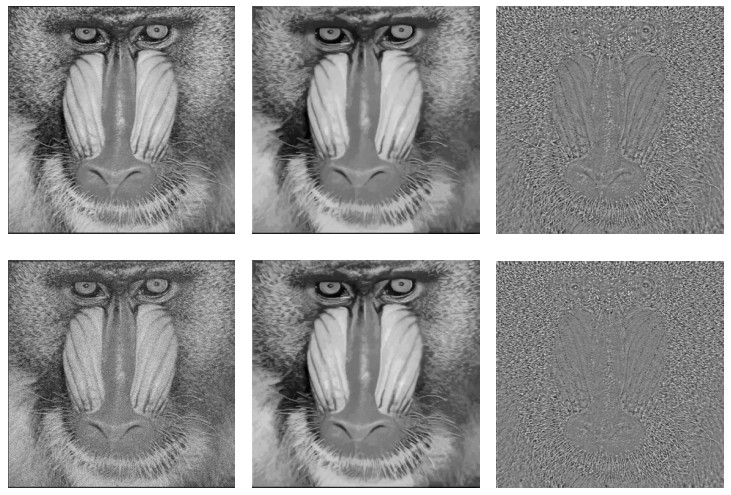
Figure 1. Images corrupted by Gaussian noise with zero mean and variance
$ \sigma^2 = 0.025 $ - Figure 2. Restored images with the proposed model.
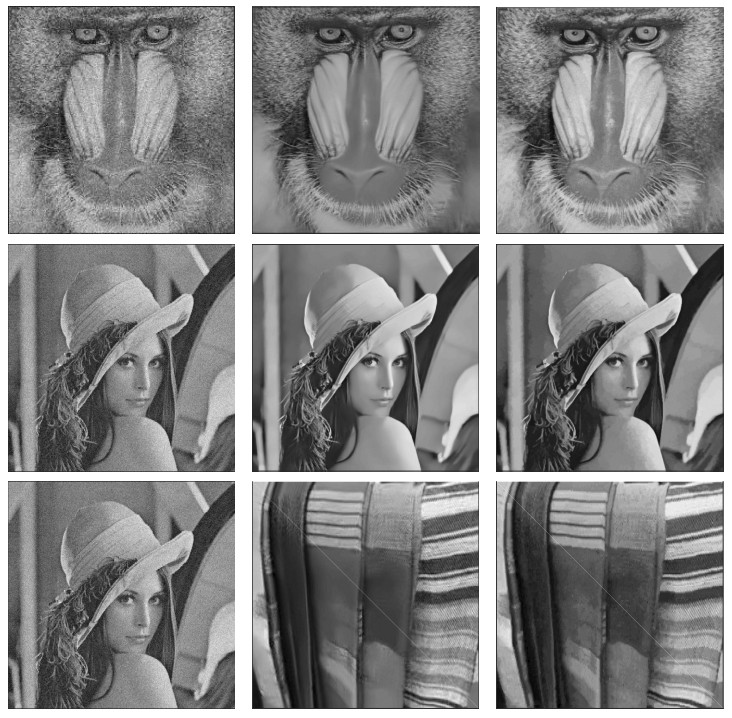
- Figure 3. First row : Noisy Lena images with noise at zero mean and different variances. Second row : Restored images using the proposed algorithm.
- Figure 4. First row : Noisy House images with noise at zero mean and different variances. Second row : Restored images using the proposed algorithm.
-
Figure 5. Left : Noisy Barbara image with
$ PSNR = 26.5544 $ , middle : Restored image by TVH with$ PSNR = 29.0488 $ and Right : Restored image by our model (NLH) with$ PSNR = 32.5609 $ . - Figure 6. Left column : Zoom of the results of TVH and right column : Zoom of the images restored using NLH.
- Figure 7. Here, we compare the texture of restored images between our model and TVH model.
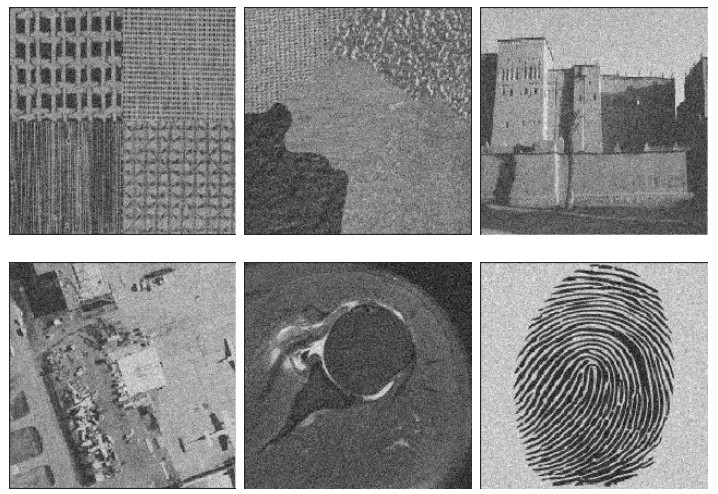
- Figure 8. Left column: Top to Bottom: Noisy image A, Noisy image B, Noisy Barbara image and Noisy image C. Middle column: Restored images by NLPL and Right column: Restored images by our proposed model.
- Figure 9. Left column : Zoom of the result of NLPL and Right column : Zoom of the image restored by our model.
- Figure 10. Left column: original image (top) and noisy image (bottom). Middle column: NLPL denoising result and error (PSNR = 27.6702). Right column: our model denoising result and error (PSNR = 28.3045).
- Figure 11. Left column: Top to Bottom: Noisy image C, Noisy Lena image, and Noisy image D. Middle column: Restored images by NLmeans and Right column: Restored images by our proposed model.