| Citation: | Ting Tan, Jing An. AN EFFICIENT NUMERICAL METHOD BASED ON LEGENDRE-GALERKIN APPROXIMATION FOR THE STEKLOV EIGENVALUE PROBLEM IN SPHERICAL DOMAIN[J]. Journal of Applied Analysis & Computation, 2021, 11(2): 587-601. doi: 10.11948/20180104 |
AN EFFICIENT NUMERICAL METHOD BASED ON LEGENDRE-GALERKIN APPROXIMATION FOR THE STEKLOV EIGENVALUE PROBLEM IN SPHERICAL DOMAIN
-
Abstract
We present in this paper an efficient numerical method based on Legendre-Galerkin approximation for the Steklov eigenvalue problem in spherical domain. Firstly, by means of spherical coordinate transformation and spherical harmonic expansion, the original problem is reduced to a sequence of equivalent one-dimensional eigenvalue problems that can be solved individually in parallel. Through the introduction of the appropriate weighted Sobolev spaces, the weak form and corresponding discrete scheme are established for each one-dimensional eigenvalue problem. Then from the approximate property of orthogonal polynomials in the weighted Sobolev spaces, we prove the error estimates of approximate eigenvalues for each one dimensional eigenvalue problem. Finally, some numerical examples are provided to illustrate the validity of our algorithms.
-

-
References
[1] A. B. Andreev and T. D. Todorov, Isoparametric finite-element approximation of a Steklov eigenvalue problem, IMA Journal of Numerical Analysis, 2004, 24, 309–322. doi: 10.1093/imanum/24.2.309 [2] M. G. Armentano and C. Padra, A posteriori error estimates for the Steklov eigenvalue problem, Appl. Numer. Math., 2008, 58, 593–601. doi: 10.1016/j.apnum.2007.01.011 [3] A. Alonso and A. D. Russo, Special approximation of variationally-posed eigenvalue problem by nonconforming methods, J. Comput. Appl. Math., 2009, 223(1), 177–197. doi: 10.1016/j.cam.2008.01.008 [4] H. J. Ahn, Vibration of a pendulum consistiting of a bob suspended from a wire: the method of integral equations, Quart. Appl. Math., 1981, 39, 109–117. doi: 10.1090/qam/613954 [5] S. Bergman and M. Schiffer, Kernel Functions and Elliptic Differential Equations in Mathematical Physics, New York, Academic Press, 1953. [6] A. Bermudez, R. Rodriguez and D. Santamarina, A finite element solution of an added mass formulation for coupled fluid-solid vibrations, Numer. Math., 2000, 87(2), 201–227. doi: 10.1007/s002110000175 [7] H. Bi and Y. Yang, A two-grid method of the non-conforming Crouzeix-Raviart element for the Steklov eigenvalue problem, Appl. Math. Comput., 2011, 217, 9669–9678. [8] H. Bi and Y. Yang, Multi-scale discretization scheme based on the Rayleigh quotient iterative method for the Steklov eigenvalue problems, Math. Prob. Eng., 2012, 539–551. [9] D. Bucur and I. Ionescu, Asymptotic analysis and scaling of friction parameters, Z. Angew. Math. Phys. (ZAMP), 2006, 57, 1–15. doi: 10.1007/s00033-006-0070-9 [10] A. P. Calderón, On an inverse boundary value problem, Seminar on Numerical Analysis and its Applications to Continuum Physics, Soc. Brasil. Mat., Rio de Janeiro, 1980, 65–73. [11] C. Conca, J. Planchard and M. Vanninathanm, Fluid and Periodic Structures, New York, John Wiley & Sons, 1995. [12] L. Cao, L. Zhang, W. Allegretto and Y. Lin, Multiscale asymptotic method for Steklov eigenvalue equations in composite media, SIAM J. Numer. Anal., 2013, 51(1), 273–296. doi: 10.1137/110850876 [13] J. F. Escobar, A comparison theorem for the first non-zero Steklov eigenvalue, J. Funct. Anal., 2000, 178(1), 143–155. doi: 10.1006/jfan.2000.3662 [14] E. M. Garau and P. Morin, Convergence and quasi-optimality of adaptive FEM for Steklov eigenvalue problems, IMA J Numer. Anal., 2011, 31, 914–946. doi: 10.1093/imanum/drp055 [15] D. B. Hinton and J. K. Shaw, Differential operators with spectral parameter incompletely in the boundary conditions, Funkc. Ekvacioj, Ser. Int., 1990, 33, 363–385. [16] X. Han, Y. Li and H. Xie, A multilevel correction method for Steklov eigenvalue problem by nonconforming finite element methods, Numer. Math-Theory Me., 2015, 8(03), 383–405. [17] Q. Lin and H. Xie, A multilevel correction type of adaptive finite element method for Steklov eigenvalue problems, Proceedings of the International Conference Applications of Mathematics, 2012, 134–143. [18] M. Li, Q. Lin and S. Zhang, Extrapolation and superconvergence of the Steklov eigenvalue problems, Adv. Comput. Math., 2010, 33, 25–44. doi: 10.1007/s10444-009-9118-7 [19] Q. Li and Y. Yang, A two-grid discretization scheme for the Steklov eigenvalue problem, J. Appl. Math. Comput., 2011, 36, 129–139. doi: 10.1007/s12190-010-0392-9 [20] Q. Li, Q. Lin and H. Xie, Nonconforming finite element approximations of the Steklov eigenvalue problem and its lower bound approximations, Appl. Numer. Math., 2013, 58, 129–151. doi: 10.1007/s10492-013-0007-5 [21] L. Ma, J. Shen and L. Wang, Spectral approximation of time-harmonic Maxwell equations in three-dimensional exterior domains, Int. J. Numer. Anal. Mod., 2015, 12(2), 1–18. [22] M. Min and D. Gottlieb, On the convergence of the Fourier approximation for eigenvalues and eigenfunctions of discontinuous problems, SIAM J. Numer. Anal., 2003, 40(6), 2254–2269. [23] J. Shen and T. Tang, Spectral and high-order methods with applications, Science Press, 2006. [24] J. Shen, T. Tang and L. Wang, Spectral Methods: Algorithms, Analysis and Applications, Springer Science and Business Media, 2011. [25] W. Tang, Z. Guan and H. Han, Boundary element approximation of Steklov eigenvalue problem for Helmhooltz equation, J. Comput. Math., 1998, 16, 165– 178. [26] H. Xie, A type of multilevel method for the Steklov eigenvalue problem, IMA J. Numer. Anal., 2014, 34(2), 592–608. doi: 10.1093/imanum/drt009 [27] Y. Yang, Q. Li and S. Li, Nonconforming finite element approximations for the Stelov eigenvalue problem, Appl. Numer. Math., 2009, 59, 2388–2401. doi: 10.1016/j.apnum.2009.04.005 [28] X. Zhang, Y. Yang and H. Bi, Spectral method with the tensor-product nodal basis for the Steklov eigenvalue problem, Math. Prob. Eng., 2013, 206–232. -
-
-
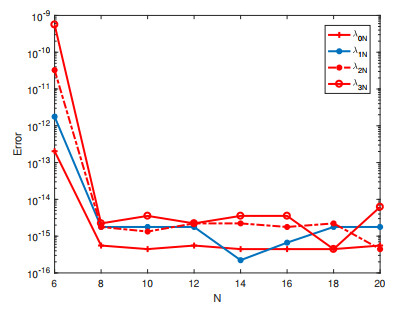
Figure 1. Errors between numerical solutions and the reference solution for
$ l = 0,1,2,3. $ -
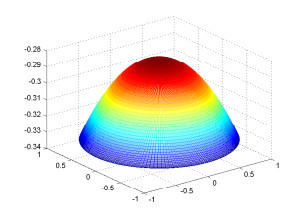
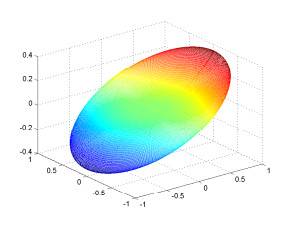
Figure 2. Mesh image of
$ real(u_0^0(r)Y_0^0(\pi/2,\phi)) $ . -
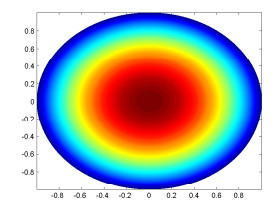
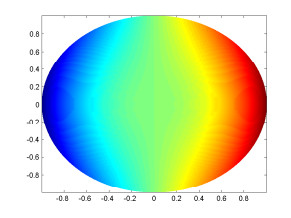
Figure 3. Contour image of
$ real(u_0^0(r)Y_0^0(\pi/2,\phi)) $ . -
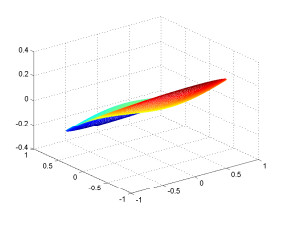
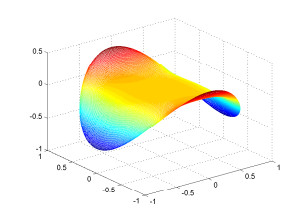
Figure 4. Mesh image of
$ real(u_1^0(r)Y_1^0(\pi/2,\phi)) $ . -
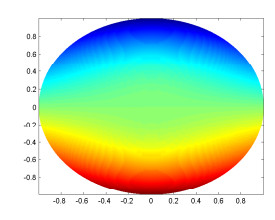
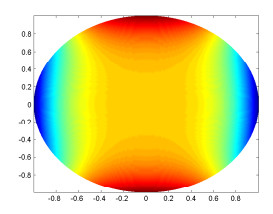
Figure 5. Contour image of
$ real(u_1^0(r)Y_1^0(\pi/2,\phi)) $ . -
Figure 6. Mesh image of
$ real(u_1^1(r)Y_1^1(\pi/2,\phi)) $ . -
Figure 7. Contour image of
$ real(u_1^1(r)Y_1^1(\pi/2,\phi)) $ . -
Figure 8. Mesh image of
$ real(u_2^0(r)Y_2^0(\pi/2,\phi)) $ . -
Figure 9. Contour image of
$ real(u_2^0(r)Y_2^0(\pi/2,\phi)) $ .




 DownLoad:
DownLoad: