| Citation: |
Lingling Liu, Ke-wei Ding, Hebai Chen. DYNAMICAL ANALYSIS OF A LOTKA-VOLTERRA LEARNING-PROCESS MODEL[J]. Journal of Applied Analysis & Computation, 2019, 9(5): 1855-1871. doi: 10.11948/20180331
|
DYNAMICAL ANALYSIS OF A LOTKA-VOLTERRA LEARNING-PROCESS MODEL
-
Abstract
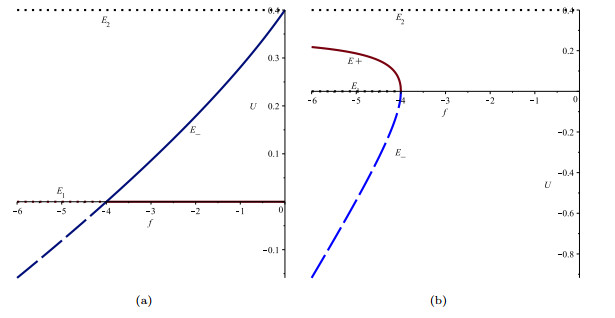
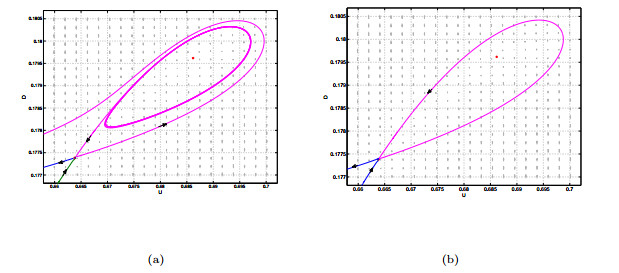
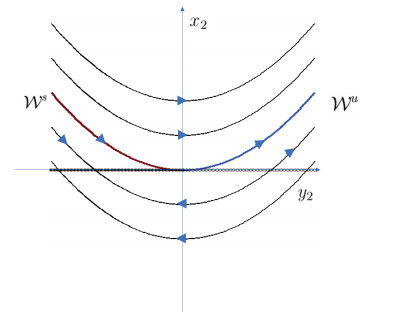
A Lotka-Volterra learning-process model was proposed by Monteiro and Notargiacomo in [Commum. Nonlinear Sci. Numer. Simulat. 47(2017), 416-420] to approach learning process as an interplay between understanding and doubt. They studied the stability of the boundary equilibria and gave some numerical simulations but no further discussion for bifurcations. In this paper, we study the qualitative properties of the interior equilibria and a singular line segment completely. Moreover, we discuss their bifurcations such as transcritical, pitchfork, Hopf bifurcation on isolated equilibria and transcritical bifurcation without parameters on non-isolated equilibria. Finally, we also demonstrate these analytical theory by numerical simulations. -
-
References
[1] C. Bordogna and E. Albano, Phase transitions in a model for social learning via the internet, Int. J. Mod. Phys. C, 2001, 12(8), 1241-1250. doi: 10.1142/S0129183101002498 [2] J. Carr, Applications of Centre Manifold Theory, New York, Springer, 1981. [3] H. Chen, S. Duan, Y. Tang and J. Xie, Global dynamics of a mechanical system with fry friction, J. Diff. Eqs., 2018, 265, 5490-5519. doi: 10.1016/j.jde.2018.06.013 [4] C. Chicone, Ordinary Differential Equations with Applications, New York, Springer, 2006. [5] S. Chow and J. Hale, Methods of Bifurcation Theory, New York, Springer, 1982. [6] Y. Kuznetsov, Elements of Applied Bifurcation Theory, New York, Springer, 1995. [7] S. Liebscher, Bifurcation without Parameters, New York, Springer, 2015. [8] L. Liu, O. Aybar, V. Romanovski and W. Zhang, Identifying weak foci and centers in the Maxwell-Bloch system, J. Math. Anal. Appl., 2015, 430, 549-571. doi: 10.1016/j.jmaa.2015.05.007 [9] F. Marton and R. Säljö, On qualitative differences in learning: I-outcome and process, Br J Educ Psychol, 1976, 46(1), 4-11. doi: 10.1111/j.2044-8279.1976.tb02980.x [10] L. Monteiro, Population dynamics in educational institutions considering the student satisfaction, Commun. Nonlinear Sci. Numer. Simulat., 2016, 30, 236-242. doi: 10.1016/j.cnsns.2015.06.015 [11] L. Monteiro and P. Notargiacomo, Learning process as an interplay between understanding and doubt: A dynamical systems approach, Commun. Nonlinear Sci. Numer. Simulat., 2017, 47, 416-420. doi: 10.1016/j.cnsns.2016.12.005 -
-
Figures(3)
Export File
Citation
Lingling Liu, Ke-wei Ding, Hebai Chen. DYNAMICAL ANALYSIS OF A LOTKA-VOLTERRA LEARNING-PROCESS MODEL[J]. Journal of Applied Analysis & Computation, 2019, 9(5): 1855-1871. doi: 10.11948/20180331
Format
Content
DownLoad:
-
Figure 1. Bifurcation diagram of system (3.14). Stable manifold
$ \mathcal{W}^s $ of the origin in red, unstable manifold$ \mathcal{W}^u $ in blue -
Figure 2. (a) Bifurcation diagram of system (2.1) for
$ \alpha = 0.4 $ ,$ \beta = 0.1 $ and$ g = -0.05 $ . (b) Bifurcation diagram of system (2.1) for$ \alpha = 0.4 $ ,$ \beta = 0.1 $ and$ g = -0.35 $ -
Figure 3. (a) A limit cycle of system (2.1) for
$ \alpha = 0.4 $ ,$ \beta = 0.111 $ ,$ f = 0.5 $ ,$ g = 0.1 $ and$ r = 0.12 $ . (b) A homoclinic loop of system (2.1) for$ \alpha = 0.4 $ ,$ \beta = 0.111 $ ,$ f = 0.5 $ ,$ g = 0.1 $ and$ r = 0.1261 $