| Citation: |
Hameed Ullah, Huafei Sun, Abdul Majeed Siddiqui, Tahira Haroon. CREEPING FLOW ANALYSIS OF SLIGHTLY NON-NEWTONIAN FLUID IN A UNIFORMLY POROUS SLIT[J]. Journal of Applied Analysis & Computation, 2019, 9(1): 140-158. doi: 10.11948/2019.140
|
CREEPING FLOW ANALYSIS OF SLIGHTLY NON-NEWTONIAN FLUID IN A UNIFORMLY POROUS SLIT
-
Abstract
This paper provides the analysis of the steady, creeping flow of a special class of slightly viscoelastic, incompressible fluid through a slit having porous walls with uniform porosity. The governing two dimensional flow equations along with non-homogeneous boundary conditions are non-dimensionalized. Recursive approach is used to solve the resulting equations. Expressions for stream function, velocity components, volumetric flow rate, pressure distribution, shear and normal stresses in general and on the walls of the slit, fractional absorption and leakage flux are derived. Points of maximum velocity components are also identified. A graphical study is carried out to show the effect of porosity and non-Newtonian parameter on above mentioned resulting expressions. It is observed that axial velocity of the fluid decreases with the increase in porosity and non-Newtonian parameter. The outcome of this theoretical study has significant importance both in industry and biosciences.-
Keywords:
- Creeping flow /
- non-Newtonian fluid /
- porous slit /
- recursive approach
-
-
References
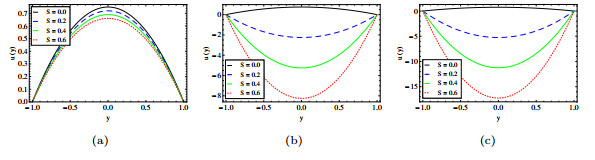
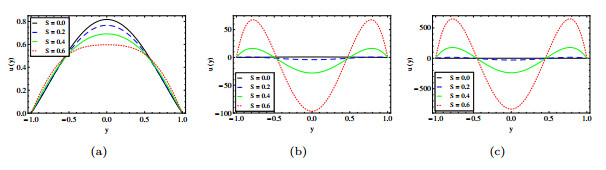
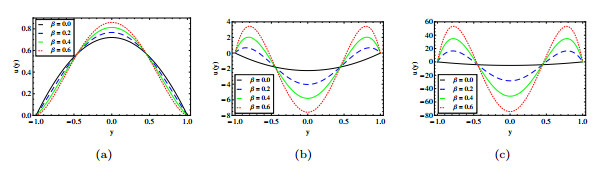
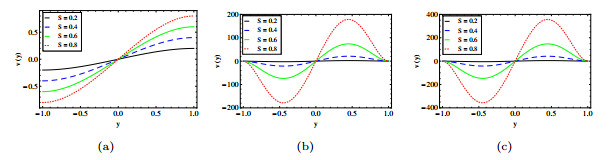
[1] S. Ahmad and N. Ahmad, On flow through renal tubule in case of periodic radial velocity component, International Journal of Emerging Multidisciplinary Fluid Sciences, 2011, 4, 201–208. [2] A. S. Berman, Laminar flow in channels with porous walls, J. Appl. Phys., 1953, 24, 1232–1235. doi: 10.1063/1.1721476 [3] J. E. Dunn and R. L. Fosdick, Thermodynamics, stability and boundedness of fluids of complexity 2 and fluids of second grade, Archs ration. Mech. Analysis, 1974, 56, 191–252. doi: 10.1007/BF00280970 [4] R. L. Fosdick and K. R. Rajagopal, Anomalous features in the model of second order fluids, Archs ration. Mech. Analysis, 1979, 70, 145–152. doi: 10.1007/BF00250351 [5] T. Haroon, A. M. Siddiqui and A. Shahzad, Creeping flow of viscous fluid through a proximal tubule with uniform reabsorption, A mathematical study, Applied Mathematical Sciences, 2016, 10(16), 795–807. [6] S. K. Karode, Laminar flow in channels with porous walls, revisited, J. Membr. Sci., 2001, 191, 237–241. doi: 10.1016/S0376-7388(01)00546-4 [7] A. Kacou, K. R. Rajagopal and A. Z. Szeri, Flow of a fluid of the differential type in a journal bearing, ASME Journal of Tribology, 1987, 109, 100–107. doi: 10.1115/1.3261298 [8] A. Kacou, K. R. Rajagopal and A. Z. Szeri, A thermodynamics analysis of journal bearings lubricated by non Newtonian fluid, ASME Journal of Tribology, 1988, 110, 414–420. doi: 10.1115/1.3261644 [9] W. E. Langlois, A recursive approach to the theory of slow steady-state viscoelastic flow, Transactions of the Society of Rheology, 1963, 7, 75–99. doi: 10.1122/1.548946 [10] W. E. Langlois, The recursive theory of slow viscoelastic flow applied to three basic problems of hydrodynamics, Transctions of the Society of Rheology, 1964, 8, 33–60. doi: 10.1122/1.548968 [11] C. W. Ng and E. Saibel, Non-linear viscosity effects in slide bearing lubrication, ASME Journal of Lubrication Technology, 1962, 7, 192–196. [12] R. S. Rivlin and J. L. Ericksen, Stress-deformation relations for istropic materials, Journal of Rational Mechanics and Analysis, 1955, 4, 323–354. [13] K. R. Rajagopal and R. L. Fosdick, Thermodynamics and stability of fluids of third grade, Proc. Roy. Soc, London, Series A, 1980, 339, 351–377. [14] K. R. Rajagopal, On the creeping flow of the second order fluid, Journal of non-Newtonian Fluid Mech., 1984, 15, 239–246. doi: 10.1016/0377-0257(84)80008-7 [15] H. G. Sharma and K. R. Singh, Numerical solution of the flow of a second order fluid through a channel with porous walls under a transverse magnetic field, Indian J. Pure and Appl. Math., 1986, 17(10), 1231-1241. [16] A. M. Siddiqui, T. Haroon and M. Kashan, MHD flow of Newtonian fluid in a permeable tubule, Magneto hydrodynamics, 2015, 51(4), 655–672. [17] A. M. Siddiqui, T. Haroon and A. Shahzad, Hydrodynamics of viscous fluid through porous slit with linear absorption, Appl. Math. Mech. Engl. Ed., 2016, 37(3), 361–378. doi: 10.1007/s10483-016-2032-6 [18] A. M. Siddiqui, and P. N. Kaloni, Certain inverse solutions of a non-Newtonian fluid, Int. J. Non-Linear Mech. 1986, 21(6), 459–473. doi: 10.1016/0020-7462(86)90042-9 [19] A. M. Siddiqui, Some more inverse solutions of a non-Newtonian fluid, Mech. Res. Commun., 1990, 17(3), 157–163. doi: 10.1016/0093-6413(90)90045-E [20] R. M. Terrill, Laminar flow in a uniformly porous channel, Aeronaut. Quart., 1964, 15, 299–310. doi: 10.1017/S0001925900010908 [21] C. Truesdell and W. Noll, The non linear fluid theories of mechanics, Handbuch der physick (ed. Fl$\ddot{u}$gge), Ⅲ/3. Berlin-Heidelberg-New York: Springer 1965. [22] S. W. Yuan, Further investigation of laminar flow in channels with porous walls, J. Appl. Phys., 1956, 27, 267–269. doi: 10.1063/1.1722355 -
-
Figures(9)
Export File
Citation
Hameed Ullah, Huafei Sun, Abdul Majeed Siddiqui, Tahira Haroon. CREEPING FLOW ANALYSIS OF SLIGHTLY NON-NEWTONIAN FLUID IN A UNIFORMLY POROUS SLIT[J]. Journal of Applied Analysis & Computation, 2019, 9(1): 140-158. doi: 10.11948/2019.140
Format
Content
DownLoad:
- Figure 1. Geometry of the Problem.
-
Figure 2. Effect of porosity parameter
$ S $ on axial velocity$ u(y) $ for$ \beta = 0, $ (a)$ x = 0.1, $ (b)$ x = 10, $ (c)$ x = 20 $ . -
Figure 3. Effect of porosity parameter
$ S $ on axial velocity$ u(y) $ for$ \beta = 0.2, $ (a)$ x = 0.1, $ (b)$ x = 10, $ (c)$ x = 20 $ . -
Figure 4. Effect of non-Newtonian parameter
$ \beta $ on axial velocity$ u(y) $ for$ S = 0.2, $ (a)$ x = 0.1, $ (b)$ x = 10, $ (c)$ x = 20 $ . -
Figure 5. Effect of porosity parameter
$ S $ on radial velocity$ v(y) $ for (a)$ \beta = 0, $ (b)$ \beta = 0.4, $ (c)$ \beta = 0.8 $ . -
Figure 6. Effect of (a) porosity parameter
$ S $ when$ \beta = 0 $ and (b)$ \beta $ when$ S = 0 $ , on pressure difference$ p(x, 0)-p(0, 0) $ . -
Figure 7. Effect of
$ S $ on (a) axial flow rate and (b) wall shear stress keeping$ \beta = 0.2 $ . Effect of$ \beta $ on (c) wall shear stress keeping$ S = 0.2 $ . -
Figure 8. Stream lines for
$ \beta = 0, $ (a)$ S = 0.2, $ (b)$ S = 0.4, $ (c)$ S = 0.8 $ . -
Figure 9. Stream lines for
$ S = 0.2 $ (a)$ \beta = 0.4, $ (b)$ \beta = 0.6, $ (c)$ \beta = 0.8 $ .