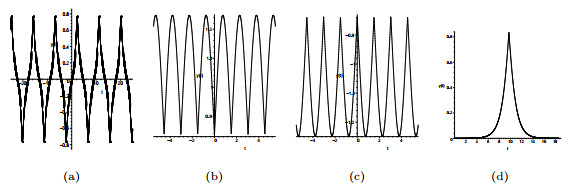
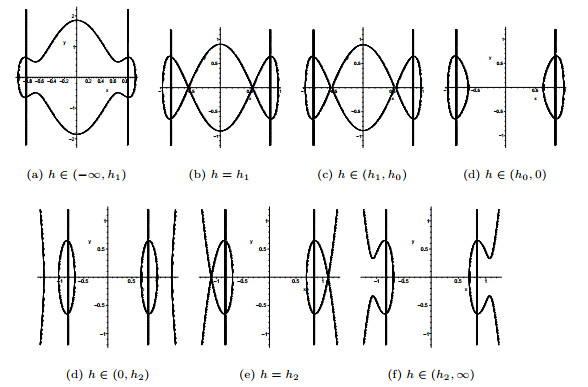
|
[1]
|
A. Biswas, A. Mirzazadeh, M. Savescu, D. Milovic, K. R. Khan, M. F. Mahmood, M. Belich, Singular solitons in optical metamaterials by ansatz method and simplest equation approach, J. of Modern Optics, 2014, 61(19), 1550–1555. doi: 10.1080/09500340.2014.944357
CrossRef Google Scholar
|
|
[2]
|
A. Biswas, R. Kaisar, K. R. Khan, M. F. Mahmood, M. Belic, Bright and dark solitons in optical metamaterials, Optik, 2014, 125, 3299–3302. doi: 10.1016/j.ijleo.2013.12.061
CrossRef Google Scholar
|
|
[3]
|
P. F. Byrd, M. D. Fridman, Handbook of Elliptic Integrals for Engineers and Sciensists, Springer, Berlin, 1971.
Google Scholar
|
|
[4]
|
J. Li, G. Chen, Bifurcations of travelling wave solutions for four classes of nonlinear wave equations, Int. J. Bifurcation and Chaos, 2005, 15(12), 3973–3998. doi: 10.1142/S0218127405014416
CrossRef Google Scholar
|
|
[5]
|
J. Li, G. Chen, On a class of singular nonlinear traveling wave equations, Int. J. Bifurcation and Chaos, 2007, 17, 4049–4065. doi: 10.1142/S0218127407019858
CrossRef Google Scholar
|
|
[6]
|
J. Li, Y. Zhang, X. Zhao, On a class of singular nonlinear traveling wave equations (Ⅱ): an example of GCKdV equations, Int. J. Bifurcation and Chaos, 2009, 19(6), 1955–2007.
Google Scholar
|
|
[7]
|
J. Li, Singular Nonlinear Traveling Wave Equations: Bifurcations and Exact Solutions, Science Press, Beijing, 2013.
Google Scholar
|
|
[8]
|
J. Li, W. Zhou, G. Chen, Understanding peakons, periodic peakons and compactons via a shallow water wave equation, Int. J. Bifurcation and Chaos, 2016, 26(12), 1650207. doi: 10.1142/S0218127416502072
CrossRef Google Scholar
|
|
[9]
|
A. Sonmezoglu, M. Yao, M. Ekici, M. Mirzazadeh, Q. Zhou, Explicit solitons in the parabolic law nonlinear negative-index materials, Nonlinear Dyn., 2017, 88, 595–607. doi: 10.1007/s11071-016-3263-6
CrossRef Google Scholar
|
|
[10]
|
Y. Xiang, X. Dai, S. Wen, J. Guo, D. Fan, Controllable Raman soliton self-frequencyshift in nonlinear metamaterials, Phys. Rev. A, 2011, 84, 033815. doi: 10.1103/PhysRevA.84.033815
CrossRef Google Scholar
|
|
[11]
|
Y. Xu, P. Suarez, D. Milovic, K. R. Khan, M. F. Mahmood, A. Biswas, M. Belic, Raman solitons in nanoscale optical waveguides, with metamaterials, having polynomial law nonlinearity, J. of Modern Optics, 2016, 63(53), 532–537.
Google Scholar
|
|
[12]
|
Q. Zhou, L. Liu, Y. Liu, H. Yu, P. Yao, C. Wei, H. Zhang, Exact optical solitons in metamaterials with cubic-quintic nonlinearity and third-order dispersion, Nonlinear Dyn., 2015, 80, 1365–1371. doi: 10.1007/s11071-015-1948-x
CrossRef Google Scholar
|
|
[13]
|
Q. Zhou, M. Mirzazadeh, M. Ekici, A. Sonmezoglu, Analytical study of solitons in non-Kerr nonlinear negative index materials, Nonlinear Dyn., 2016, 86, 623–638. doi: 10.1007/s11071-016-2911-1
CrossRef Google Scholar
|
|
[14]
|
Y. Zhou, J. Li, Exact Solutions and Dynamics of the Raman Soliton Model in Nanoscale Optical Waveguides, with Metamaterials, Having Polynomial Law Non-Linearity, Int. J. Bifurcation and Chaos, 2017, 27(12), 1750188. doi: 10.1142/S0218127417501887
CrossRef Google Scholar
|




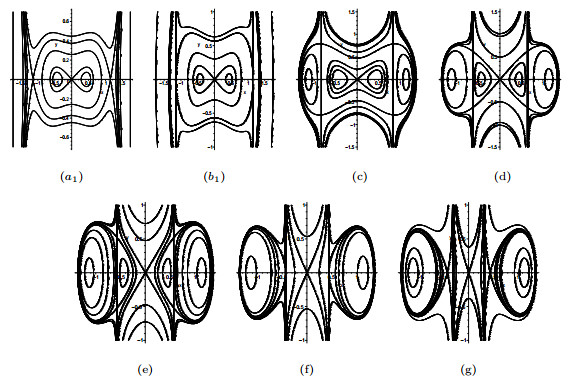

 DownLoad:
DownLoad: