| Citation: |
Jinting Ha, Huiqun Zhang, Qiulan Zhao. EXACT SOLUTIONS FOR A DIRAC-TYPE EQUATION WITH N-FOLD DARBOUX TRANSFORMATION[J]. Journal of Applied Analysis & Computation, 2019, 9(1): 200-210. doi: 10.11948/2019.200
|
EXACT SOLUTIONS FOR A DIRAC-TYPE EQUATION WITH N-FOLD DARBOUX TRANSFORMATION
-
Abstract
Based on matrix spectral problems associated with the real special orthogonal Lie algebra so(3, $\mathbb{R}$), a Dirac-type equation is derived by virtue of the zero-curvature equation. Further, an N-fold Darboux transformation for the Dirac-type equation is constructed by means of the gauge transformation. Finally, as its application, some exact solutions and their figures are obtained via symbolic computation software (Maple). -
-
References
[1] A. D. Alhaidari, H. Bahlouli and I.A. Assi, Solving Dirac equation using the tridiagonal matrix representation approach, Phys. Lett. A., 2016, 380, 1577–1581. doi: 10.1016/j.physleta.2016.03.001 [2] R. Beerwerth and H. Bauke, Krylov subspace methods for the Dirac equation, Comput. Phys. Commun., 2015, 188, 189–197. doi: 10.1016/j.cpc.2014.11.008 [3] G. W. Bluman and S. Kumei, Symmetries and Differential Equations, Springer-Verlag, World Publishing Corp, 1989. [4] B. J. Cantwell, Introduction to Symmetry Analysis, Cambridge University Press, Cambridge, 2002. [5] J. C. Chen, Z. Y. Ma, Y. H. Hu, Nonlocal symmetry, Darboux transformation and soliton-cnoidal wave interaction solution for the shallow water wave equation, J. Math. Anal. Appl., 2018, 460, 987–1003. doi: 10.1016/j.jmaa.2017.12.028 [6] S. T. Chen and W. X. Ma, Lump solutions to a generalized Bogoyavlensky-Konopelchenko equation, Front. Math. China, 2018, 13(3), 525–534. doi: 10.1007/s11464-018-0694-z [7] H. H. Dong, et al, A new integrable symplectic map and the lie point symmetry associated with nonlinear lattice equations, J. Nonlinear. Sci. Appl., 2016, 9, 5107–5118. doi: 10.22436/jnsa [8] E. G. Fan, Extended tanh-funtion method and its applications to nonlinear equations, Phys. Lett. A., 2000, 277, 212–218. doi: 10.1016/S0375-9601(00)00725-8 [9] X. G. Geng, J. Shen and B. Xue, A new nonlinear wave equation: Darboux transformation and soliton solutions, Wave Motion, 2002, 35, 71–90. doi: 10.1016/S0165-2125(01)00078-6 [10] C. H. Gu and Z. X. Zhou, On Darboux transformations for soliton equations in high-dimensional spacetime, Lett. Math. Phys., 1994, 32, 1-10. doi: 10.1007/BF00761119 [11] M. Guo, et al, A new ZK-ILW equation for algebraic gravity solitary waves in finite depth stratified atmosphere and the research of squall lines formation mechanism, Comput. Mathe. Appli., 2018, 75, 3589–3603. doi: 10.1016/j.camwa.2018.02.019 [12] J. H. He and M. A. Abdou, New periodic solutions for nonlinear evolution equations using exp-function method, Chaos Solitons Fractals., 2007, 34, 1421–1429. doi: 10.1016/j.chaos.2006.05.072 [13] J. H. He and X. H. Wu, Exp-function method for nonlinear wave equations, Chaos Solitons Fract., 2006, 30, 700–708. doi: 10.1016/j.chaos.2006.03.020 [14] R. Hirota, The Direct Method in Soliton Theory, Cambridge University Press, Cambridge, 2004. [15] Y. Hou, E. G. Fan and Z. J. Qiao, The algebro-geometric solutions for the Fokas-Olver-Rosenau-Qiao (FORQ) hierarchy, J. Geo. Phys., 2017, 117, 105–133. doi: 10.1016/j.geomphys.2017.03.004 [16] Q. C. Ji and K. Zhu, Solvability of Dirac type equations, Adv. Math., 2017, 320, 451–474. doi: 10.1016/j.aim.2017.08.040 [17] H. B. Lan and K. L. Wang, Exact solutions for two nonlinear equations: I, J. Phys. A: Math. Gen., 1990, 23, 3923–3928. doi: 10.1088/0305-4470/23/17/021 [18] X. Y. Li, et al, Binary Bargmann symmetry constraint associated with 3 $times$ 3 discrete matrix spectral problem, J. Nonlinear. Sci. Appl., 2015, 8(5), 496–506. doi: 10.22436/jnsa CrossRef $times$ 3 discrete matrix spectral problem" target="_blank">Google Scholar
[19] X. Y. Li and Q. L. Zhao, A new integrable symplectic map by the binary nonlinearization to the super AKNS system, J. Geo. Phys., 2017, 121, 123–137. doi: 10.1016/j.geomphys.2017.07.010 [20] S. K. Liu, et al, Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations, Phys. Lett. A., 2001, 289, 69–74. doi: 10.1016/S0375-9601(01)00580-1 [21] W. X. Ma, Diversity of interaction solutions to the (2 + 1)-dimensional Ito equation, Comput. Math. Appl., 2018, 75, 289–295. doi: 10.1016/j.camwa.2017.09.013 [22] W. X. Ma, Abundant lumps and their interaction solutions of (3 + 1)-dimensional linear PDEs, J. Geom. Phys., 2018, 133, 10–16. doi: 10.1016/j.geomphys.2018.07.003 [23] W. X. Ma, Trigonal curves and algebro-geometric solutions to soliton hierarchies I, P. Roy. Soc. A., 2017, 473, 20170232. doi: 10.1098/rspa.2017.0232 [24] W. X. Ma, Complexiton solutions to the Korteweg-de Vries equation, Phys. Lett. A., 2002, 301, 35–44. doi: 10.1016/S0375-9601(02)00971-4 [25] W. X. Ma, Darboux transformations for a Lax integrable system in 2n dimensions, Lett. Math. Phys., 1997, 39, 33–49. doi: 10.1007/s11005-997-3049-3 [26] W. X. Ma, A soliton hierarchy associated with so(3, $\mathbb{R}$), Appl. Math. Comput., 2013, 220, 117–122. [27] W. X. Ma, An explicit symmetry constraint for the Lax pairs and the adjoint Lax pairs of AKNS systems, Phys. Lett. A., 1994, 185, 277–286. doi: 10.1016/0375-9601(94)90616-5 [28] W. X. Ma and B. Fuchssteiner, Explicit and exact solutions to a Kolmogorov-Petrovskii-Piskunov equation, Int. J. Non-Linear Mech., 1996, 31, 329–338. doi: 10.1016/0020-7462(95)00064-X [29] W. X. Ma, J. S. He and Z. Y. Qin, A supertrace identity and its applications to superintegrable systems, J. Math. Phys., 2008, 49, 033511. doi: 10.1063/1.2897036 [30] W. X. Ma, T. W. Huang and Y. Zhang, A multiple exp-function method for nonlinear differential equations and its application, Phys. Scr., 2010, 82, 065003. doi: 10.1088/0031-8949/82/06/065003 [31] W. X. Ma and J. H. Lee, A transformed rational function method and exact solutions to the 3 + 1 dimensional Jimbo-Miwa equation, Chaos Solitons Fract., 2009, 42, 1356–1363. doi: 10.1016/j.chaos.2009.03.043 [32] W. X. Ma and Y. J. Zhang, Darboux transformations of integrable couplings and applications, Rev. Math. Phys., 2018, 30, 1850003. doi: 10.1142/S0129055X18500034 [33] W. X. Ma and Y. Zhou, Lump solutions to nonlinear partial differential equations via Hirota bilinear forms, J. Differ. Equations, 2018, 264(4), 2633–2659. doi: 10.1016/j.jde.2017.10.033 [34] S. Manukure, Y. Zhou and W. X. Ma, Lump solutions to a (2 + 1)-dimensional extended KP equation, Comput. Math. Appl., 2018, 75, 2414–2419. doi: 10.1016/j.camwa.2017.12.030 [35] E. J. Parkes and B. R. Duffy, An automated tanh-function method for finding solitary wave solutions to non-linear evolution equations, Comput. Phys. Commun., 1996, 98, 288–300. doi: 10.1016/0010-4655(96)00104-X [36] S. F. Shen, et al, New soliton hierarchies associated with the Lie algebra so(3, $mathbb{R}$) and the bi-Hamiltonian structures, Rep. Math. Phys., 2015, 75, 113–133. doi: 10.1016/S0034-4877(15)60028-3 CrossRef $mathbb{R}$) and the bi-Hamiltonian structures" target="_blank">Google Scholar
[37] V. M. Simulik and I. Yu. Krivsky, Bosonic symmetries of the Dirac equation, Phys. Lett. A., 2011, 375, 2479–2483. doi: 10.1016/j.physleta.2011.03.058 [38] G. Z. Tu, The trace identity, a powerful tool for constructing the Hamiltonian structure of integrable systems, J. Math. Phys., 1989, 30, 330–338. doi: 10.1063/1.528449 [39] M. L. Wang, Solitary wave solutions for variant Boussinesq equations, Phys. Lett. A., 1995, 199, 169–172. doi: 10.1016/0375-9601(95)00092-H [40] M. L. Wang, Exact solutions for a compound KdV-Burgers equation, Phys. Lett. A., 1996, 213, 279–287. doi: 10.1016/0375-9601(96)00103-X [41] H. Wang, Lump and interaction solutions to the (2+1)-dimensional Burgers equation, Appl. Mathe. Lett., 2018, 85, 27–34. doi: 10.1016/j.aml.2018.05.010 [42] A. M. Wazwaz, The tanh-coth method for solitons and kink solutions for nonlinear parabolic equations, Appl. Math. Comput., 2007, 188, 1467–1475. [43] X. X. Xu, An integrable coupling hierarchy of Dirac integrable hierarchy, its Liouville integrability and Darboux transformation, J. Nonlinear Sci. Appl., 2017, 10, 3328–3343. doi: 10.22436/jnsa [44] B. Xue, F. Li and H. Y. Wang, Darboux transformation and conservation laws of a integrable evolution equations with 3 × 3 Lax pairs, Appl. Math. comput., 2015, 269, 326–331. [45] H. W. Yang, et al, A new ZK-BO equation for three-dimensional algebraic Rossby solitary waves and its solution as well as fission property, Nonlinear Dyn., 2018, 91, 2019–2032. doi: 10.1007/s11071-017-4000-5 [46] J. Y. Yang, W. X. Ma and Z. Y. Qin, Lump and lump-soliton solutions to the (2 + 1)-dimensional Ito equation, Anal. Math. Phys., 2018, 8, 427–436. doi: 10.1007/s13324-017-0181-9 [47] H. X. Yang, X. X. Xu and H. Y. Ding, Two hierarchies of lattice soliton equations associated with a new discrete eigenvalue problem and Darboux transformation, Phys. Lett. A., 2015, 338, 117–127. [48] Y. J. Ye, et al, A generalized Dirac soliton hierarchy and its bi-Hamiltonian structure, Appl. Math. Lett., 2016, 60, 67–72. doi: 10.1016/j.aml.2016.04.010 [49] H. Q. Zhang and W. X. Ma, Extended transformed rational function method and applications to complexiton solutions, Appl. Math. Comput., 2014, 230, 509–515. [50] J. B. Zhang and W. X. Ma, Mixed lump-kink solutions to the BKP equation, Comput. Math. Appl., 2017, 74, 591–596. doi: 10.1016/j.camwa.2017.05.010 [51] H. Q. Zhao and W. X. Ma, Mixed lump-kink solutions to the KP equation, Comput. Math. Appl., 2017, 74, 1399–1405. doi: 10.1016/j.camwa.2017.06.034 [52] Q. L. Zhao, X. Y. Li and F. S. Liu, Two integrable lattice hierarchies and their respective Darboux transformations, Appl. Math. Comput., 2013, 219(10), 5693–5705. [53] Q. Zhao and L. H. Wu, Darboux transformation and explicit solutions to the generalized TD equation, Appl. Math. Lett., 2017, 67, 1–6. doi: 10.1016/j.aml.2016.11.012 [54] Q. L. Zhao and X. Y. Li, A Bargmann system and the involutive solutions associated with a new 4-Order lattice hierarchy, Anal. Math. Phys., 2016, 6(3), 237–254. [55] Y. B. Zhou, M. L. Wang and Y. M. Wang, Periodic wave solutions to a coupled KdV equations with variable coefficients, Phys. Lett. A., 2003, 208, 31–36. -
-
Figures(2)
Export File
Citation
Jinting Ha, Huiqun Zhang, Qiulan Zhao. EXACT SOLUTIONS FOR A DIRAC-TYPE EQUATION WITH N-FOLD DARBOUX TRANSFORMATION[J]. Journal of Applied Analysis & Computation, 2019, 9(1): 200-210. doi: 10.11948/2019.200
Format
Content
DownLoad:
-
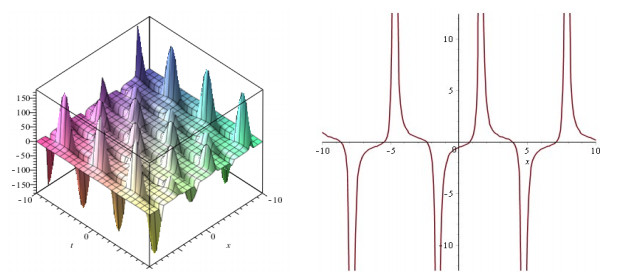
Figure 1. Plots of the intensity distribution
$ \hat p $ and the solution$ \hat p $ at$ t = 0 $ of Eq. (1.1) with$ {\lambda _1} = {\lambda _2} = 1, \ {\lambda _3}{\rm{ = - 1}}, \ \gamma _1^{(2)} = 0, \ \gamma _1^{(1)} = \gamma _3^{(2)} = 1, \ \gamma _2^{(1)} = \gamma _2^{(2)} = \gamma _3^{(1)} = - 1. $ . -
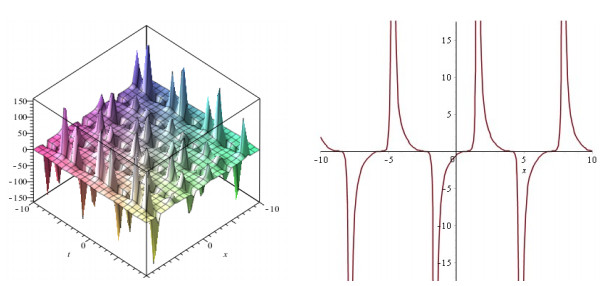
Figure 2. Plots of the intensity distribution
$ \hat q $ and the solution$ \hat q $ at$ t = 0 $ of Eq. (1.1) with$ {\lambda _1} = {\lambda _2} = 1, \ {\lambda _3}{\rm{ = - 1}}, \ \gamma _1^{(2)} = 0, \ \gamma _1^{(1)} = \gamma _3^{(2)} = 1, \ \gamma _2^{(1)} = \gamma _2^{(2)} = \gamma _3^{(1)} = - 1. $ .