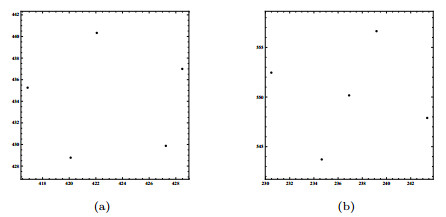
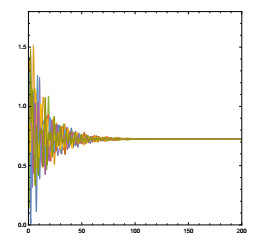
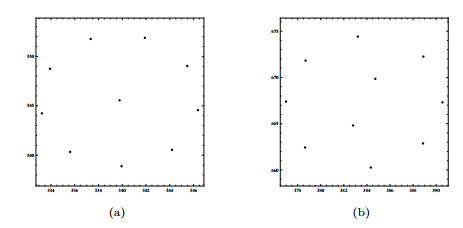
|
[1]
|
F. Cucker and S. Smale, Emergent behavior in flocks, IEEE Transactions on Automatic Control, 2007, 52(5), 852–862. doi: 10.1109/TAC.2007.895842
CrossRef Google Scholar
|
|
[2]
|
F. Cucker and S. Smale, On the mathematics of emergence, Japanese Journal of Mathematics, 2007, 2(1), 197–227. doi: 10.1007/s11537-007-0647-x
CrossRef Google Scholar
|
|
[3]
|
F. Cucker and J. G. Dong, A general collision-avoiding flocking framework, IEEE Transactions on Automatic Control, 2011, 56(5), 1124–1129. doi: 10.1109/TAC.2011.2107113
CrossRef Google Scholar
|
|
[4]
|
Y. P. Choi and Z. C. Li, Emergent behavior of Cucker-Smale flocking particles with heterogeneous time delays, Applied Mathematics Letters, 2018, 86, 49–56. doi: 10.1016/j.aml.2018.06.018
CrossRef Google Scholar
|
|
[5]
|
P. Cristina and R. V. Irene, Flocking estimates for the Cucker-Smale model with time lag and hierarchical leadership, Journal of Mathematical Analysis and Applications, 2018, 464(2), 1313–1332.
Google Scholar
|
|
[6]
|
S. Y. Ha and J. G. Liu, A simple proof of the Cucker-Smale flocking dynamics and mean-field limit, Communications in Mathematical Sciences, 2008, 7(2), 297–325.
Google Scholar
|
|
[7]
|
J. H. Kang, S. Y. Ha, K. Kang and E. Jeong, How do cultural classes emerge from assimilation and distinction? An extension of the Cucker-Smale flocking model, Journal of Mathematical Sociology, 2014, 38(1), 47–71.
Google Scholar
|
|
[8]
|
I. Markou, Collision-avoiding in the singular Cucker-Smale model with nonlinear velocity couplings, Discrete and Continuous Dynamical Systems, 2018, 38(10), 5245–5260. doi: 10.3934/dcds.2018232
CrossRef Google Scholar
|
|
[9]
|
R. Olfati-Saber, Flocking for multi-agent dynamic systems: algorithms and theory, IEEE Transactions on Automatic Control, 2006, 51(3), 401–420. doi: 10.1109/TAC.2005.864190
CrossRef Google Scholar
|
|
[10]
|
C. Pignotti and E. Trlat, Convergence to consensus of the general finite-dimensional Cucker-Smale model with time-varying delays, 2017, ArXiv: 1707.05020 v2.
Google Scholar
|
|
[11]
|
J. Park, H. J. Kim and S. Y. Ha, Cucker-Smale flocking with inter-particle bonding forces, IEEE Transactions on Automatic Control, 2010, 55(11), 2617–2623. doi: 10.1109/TAC.2010.2061070
CrossRef Google Scholar
|
|
[12]
|
V. M. Popov and M. R. Posehn, Hyperstability of control systems, Journal of Dynamic Systems Measurement and Control, 1974, 96(3), 372.
Google Scholar
|
|
[13]
|
C. W. Reynolds, Flocks, herds and schools: A distributed behavioral model, ACM SIGGRAPH Computer Graphics, 1987, 21(4), 25–34. doi: 10.1145/37402.37406
CrossRef Google Scholar
|
|
[14]
|
Y. Sun, D. Zhao and J. Ruan, Consensus in noisy environments with switching topology and time-varying delays, Physica A Statistical Mechanics and Its Applications, 2010, 389(19), 4149–4161. doi: 10.1016/j.physa.2010.05.038
CrossRef Google Scholar
|
|
[15]
|
Y. Sun and R. Jiong, Synchronization between two different chaotic systems with noise perturbation, Chinese Physics B, 2010, 19(7), 150–155.
Google Scholar
|
|
[16]
|
Y. Sun, W. Li and D. Zhao, Outer synchronization between two complex dynamical networks with discontinuous coupling, Chaos, 2012, 22(4), 043125. doi: 10.1063/1.4768661
CrossRef Google Scholar
|
|
[17]
|
T. Vicsek, A. Czirk, E. Benjacob, et al, Novel type of phase transition in a system of self-driven particles, Physical Review Letters, 1995, 75(6), 1226. doi: 10.1103/PhysRevLett.75.1226
CrossRef Google Scholar
|
|
[18]
|
X. Wang, L. Wang and J. H. Wu, Impacts of time delay on flocking dynamics of a two-agent flock model, Commun. Nonlinear. Sci., 2019, 70, 80–88. doi: 10.1016/j.cnsns.2018.10.017
CrossRef Google Scholar
|
|
[19]
|
W. Yu, G. Chen and M. Cao, Distributed leader-follower flocking control for multi-agent dynamical systems with time-varying velocities, Systems Control Letters, 2010, 59(9), 543–552. doi: 10.1016/j.sysconle.2010.06.014
CrossRef Google Scholar
|




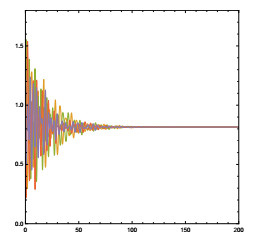

 DownLoad:
DownLoad: