| Citation: |
Shaoli Wang, Fei Xu. Analysis of an HIV model with post-treatment control[J]. Journal of Applied Analysis & Computation, 2020, 10(2): 667-685. doi: 10.11948/20190081
|
Analysis of an HIV model with post-treatment control
-
Abstract
Recent investigation indicated that latent reservoir and immune impairment are responsible for the post-treatment control of HIV infection. In this paper, we simplify the disease model with latent reservoir and immune impairment and perform a series of mathematical analysis. We obtain the basic infection reproductive number $ R_{0} $ to characterize the viral dynamics. We prove that when $ R_{0}<1 $, the uninfected equilibrium of the proposed model is globally asymptotically stable. When $ R_{0}>1 $, we obtain two thresholds, the post-treatment immune control threshold and the elite control threshold. The model has bistable behaviors in the interval between the two thresholds. If the proliferation rate of CTLs is less than the post-treatment immune control threshold, the model does not have positive equilibria. In this case, the immune free equilibrium is stable and the system will have virus rebound. On the other hand, when the proliferation rate of CTLs is greater than the elite control threshold, the system has stable positive immune equilibrium and unstable immune free equilibrium. Thus, the system is under elite control. -
-
References
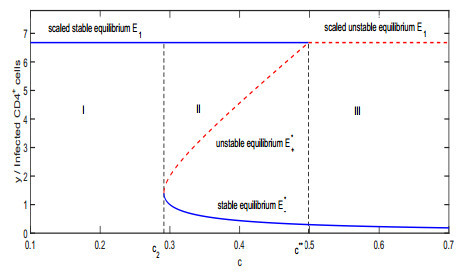
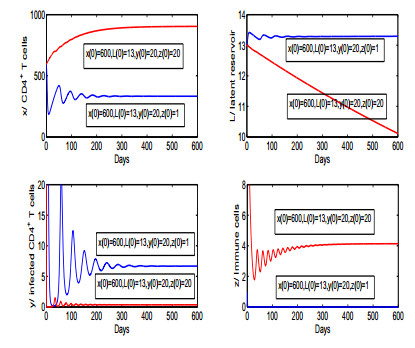
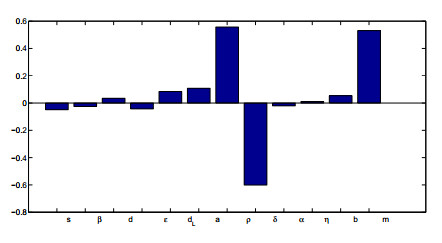
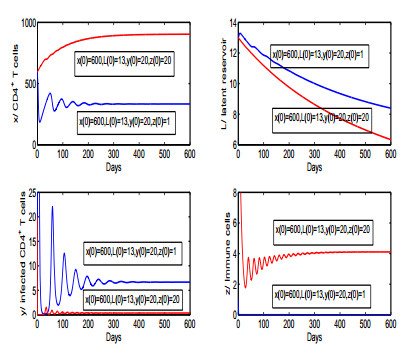
[1] "Mississippi baby" now has detectable HIV, researchers find, National Institutes of Health News. July 10, 2014. Available at www.niaid.nih.gov/news/newsreleases/2014/pages/mississippibabyhiv.aspx. [2] C. L. Althaus and R. J. De Boer, Dynamics of immune escape during HIV/SIV infection. PLoS Comput. Biol., 2008, 4. E1000103. [3] E. Avila-Vales, N. Chan-Chi and G. Garcia-Almeida, Analysis of a viral infection model with immune impairment, intracellular delay and general non-linear incidence rate, Chaos Solitons Fractals, 2014, 69, 1-9. [4] C. Bartholdy, J. P. Christensen, D. Wodarz and A. R. Thomsen, Persistent virus infection despite chronic cytotoxic T-lymphocyte activation in Gamma interferon-deficient mice infection with lymphocytic choriomeningitis virus, J. Virol., 2000, 74, 1034-10311. [5] S. M. Blower and H. Dowlatabadi, Sensitivity and uncertainty analysis of complex models of disease transmission: an HIV model. as an example, Int. Stat. Rev., 1994, 2, 229-243. [6] S. Bonhoeffer and G. M. N. D. F. Rembiszewski M, Ortiz, Risks and benefits of structured antiretroviral drug therapy interruptions in HIV-1 infection, AIDS, 2000, 14, 2313-2322. [7] D. Burg, L. Rong, A. U. Neumann and H. Dahari, Mathematical modeling of viral kinetics under immune control during primary HIV-1 infection, J. Theor. Biol., 2009, 259, 751-759. doi: 10.1016/j.jtbi.2009.04.010 [8] R. J. De Boer and A. S. Perelson, Target cell limited and immune control models of HIV infection: A comparison., J. Theor. Biol., 1998, 190, 201-214. doi: 10.1006/jtbi.1997.0548 [9] S. Chen, Z. Liu and J. Shi, Nonexistence of nonconstant positive steady states of a diffusive predator-prey model with fear effect, J. Nonlinear Modeling and Analysis, 2019, 1(1), 47-56.}, , [10] M. J. Churchill, S. G. Deeks, D. M. Margolis et al., HIV reservoirs: what, where and how to target them, Nature Reviews Microbiology, 2016, 14, 55-60. [11] K. E. Clarridge, J. Blazkova, K. Einkauf et al., Effect of analytical treatment interruption and reinitiation of antiretroviral therapy on HIV reservoirs and immunologic parameters in infected individuals, PLoS Pathog, 2018, 14. E1006792. [12] J. M. Conway and A. S. Perelson, Post-treatment control of HIV infection. proc, Natl. Acad. Sci. USA, 2015, 112, 5467-5472. doi: 10.1073/pnas.1419162112 [13] R. V. Culshaw and S. Ruan, A delay-differential equation model of HIV infection of CD4$^{+}$ T-cells., Math. Biosci., 2000, 165, 27-39. doi: 10.1016/S0025-5564(00)00006-7 [14] H. Doekes, C. Fraser and K. Lythgoe, Effect of the latent reservoir on the evolution of HIV at the within- and between-host levels., PLoS Comput Biol, 2017, 13. E1005228. doi: 10.1371/journal.pcbi.1005228 [15] C. Gavegnano, J. H. Brehm, F. P. Dupuy et al., Novel mechanisms to inhibit HIV reservoir seeding using Jak inhibitors, PLOS Pathogens, 2017, 13. E1006740. [16] J. Hale and S. M. Verduyn Lunel, Introduction to functional differential equations, Springer, New York, 1993. [17] D. D. Ho, A. U. Neumann, A. S. Perelson et al., Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection, Nature, 1995, 373, 123-126. [18] Z. Hu, J. Zhang, H. Wang et al., Dynamics analysis of a delayed viral infection model with logistic growth and immune impairment, Appl. Math. Model., 2014, 38, 524-534. [19] S. Iwami, T. Miura, S. Nakaoka and Y. Takeuchi, Immune impairment in HIV infection: Existence of risky and immunodeficiency thresholds, J. Theor. Biol., 2009, 260, 490-501. doi: 10.1016/j.jtbi.2009.06.023 [20] S. Iwami, S. Nakaoka, Y. Takeuchi and T. Miura, Immune impairment thresholds in HIV infection., Immunol. Lett., 2009, 123, 149-154. doi: 10.1016/j.imlet.2009.03.007 [21] H. Kim and A. S. Perelson, Dynamic characteristics of HIV-1 reservoirs., Curr. Opin. HIV AIDS, 2006, 1, 152-156. [22] H. Kim and A. S. Perelson, Viral and latent reservoir persistence in HIV-1-infected patients on therapy., PLoS Comput. Biol., 2006, 2. E135. doi: 10.1371/journal.pcbi.0020135 [23] N. N. Krasovskii, Problems of the theory of stability of motion, (Russian), (1959). English translation, Stanford University Press, Stanford, CA, 1963. [24] J. P. LaSalle, Some extensions of liapunov's second method, IRE Transactions on Circuit Theory, 1960, CT-7, 520-527. [25] M. Li and H. Shu, Multiple stable periodic oscillations in a mathematical model of CTL response to htlv-i infection, Bull. Math. Biol., 2011, 73, 1774-1793. doi: 10.1007/s11538-010-9591-7 [26] S. Marino, I. B. Hogue, C. J. Ray and D.E. Kirschner.A methodology for performing global uncertainty and sensitivity analysis in systems biology, Journal of Theoretical Biology, 2008, 254(1), 178-196. [27] M. Markowitz, M. Louie, A. Hurley et al., A novel antiviral intervention results in more a urate assessment of human immunodeficiiency virus type 1 replication dynamics and T-cell decay in vivo., J. Virol, 2003, 77, 5037-5038. [28] P. W. Nelson and A. S. Perelson, Mathematical analysis of a delay differential equation models of HIV-1 infection, Math. Biosci., 2002, 179, 73-94. doi: 10.1016/S0025-5564(02)00099-8 [29] M. A. Nowak and C. R. M. Bangham, Population dynamics of immune response to persistent viruses, Science, 1996, 272, 74-79. doi: 10.1126/science.272.5258.74 [30] M. A. Nowak, R. M. May, R. E. Phillips et al., Antigenic oscillations and shifting immunodominance in HIV-1 infections, Nature, 1995, 375, 606-611. [31] D. Persaud, H. Gay, C. Ziemniak et al., Absence of detectable HIV-1 viremia after treatment cessation in an infant, N. Engl. J. Med., 2013, 369, 1828-1835. [32] A. Pugliese and A. Gandolfi, Asimple model of pathogen-immunedynamics including specific andnon-specific immunity, Math. Biosci., 2008, 214, 73-80. doi: 10.1016/j.mbs.2008.04.004 [33] R. R. Regoes, D. Wodarz and M. A. Nowak, Virus dynamics: the effect of target cell limitation and immune responses on virus evolution, J. Theor. Biol., 1998, 191, 451-462. doi: 10.1006/jtbi.1997.0617 [34] L. Rong and A. S. Perelson, Modeling HIV persistence, the latent reservoir, and viral blips, J. Theor. Biol., 2009, 260, 308-331. doi: 10.1016/j.jtbi.2009.06.011 [35] L. Rong, and A.S. Perelson, Asymmetric division of activated latently infected cells may explain the decay kinetics of the HIV-1 latent reservoir and intermittent viral blips, Math. Biosci., 2009, 217, 77-87. doi: 10.1016/j.mbs.2008.10.006 [36] Z. Rubinstein, A Course in Ordinary and Partial Differential Equations, Academic Press, New York, 1969. [37] X. Song, S. Wang and X. Zhou, Stability and hopf bifurcation for a viral infection model with delayed non-lytic immune response., J. Appl. Math. Comput., 2010, 33, 251-265. [38] B. Tang, Y. Xiao, R. A. Cheke and N. Wang, Piecewise virus-immune dynamic model with HIV-1 rna-guided therapy, J. Theor. Biol., 2015, 377, 36-46. doi: 10.1016/j.jtbi.2015.03.040 [39] G. C. Treasure, E. Aga, R. J. Bosch et al., Relationship among viral load outcomes in HIV treatment interruption trials, J Acquir Immune Defic Syndr., 2016, 72, 310-313. [40] S. Wang and L. Rong, Stochastic population switch may explain the latent reservoir stability and intermittent viral blips in HIV patients on suppressive therapy, J. Theor. Biol., 2014, 360, 137-148. doi: 10.1016/j.jtbi.2014.06.042 [41] K. Wang, W. Wang and X. Liu, Global stability in a viral infection model with lytic and nonlytic immune response, J. Comput. Appl. Math., 2007, 51, 1593-1610. [42] K. Wang, W. Wang, H. Pang and X. Liu, Complex dynamic behavior in a viral model with delayed immune response, Phys. D, 2007, 226, 197-208. doi: 10.1016/j.physd.2006.12.001 [43] S. Wang and F. Xu, Thresholds and bistability in virus-immune dynamics, Applied Mathematics Letters, 2018, 78, 105-111. doi: 10.1016/j.aml.2017.11.002 [44] S. Wang, F. Xu and L. Rong, bistability analysis of an hiv model with immune response, Journal of Biological Systems, 2017, 25, 677-695. doi: 10.1142/S021833901740006X [45] S. Wang, X. Song and Z. Ge, Dynamics analysis of a delayed viral infection model with immune impairment, Appl. Math. Model., 2011, 35, 4877-4885. doi: 10.1016/j.apm.2011.03.043 [46] X. Wang, Y. Tao and X. Song, A delayed HIV-1 infection model with beddington-deangelis functional response, Nonlinear Dyn., 2010, 62, 67-72. doi: 10.1007/s11071-010-9699-1 [47] Z. Wang and X. Liu, A chronic viral infection model with immune impairment, J. Theor. Biol., 2007, 249, 532-542. doi: 10.1016/j.jtbi.2007.08.017 [48] X. Wei, S. K. Ghosh, M. E. Taylor et al., Viral dynamics in human immunodeficiency virus type 1 infection, Nature, 1995, 373, 117-122. [49] D. Wodarz, J. P. Christensen and A. R. Thomsen, The importance of lytic and nonlytic immune response in viral infections, Trends Immunol, 2002, 23, 194-200. doi: 10.1016/S1471-4906(02)02189-0 [50] Y. Xiao, S. Tang, Y. Zhou et al., Predicting the hiv/aids epidemic and measuring the effect of mobility in mainland china, Journal of Theoretical Biology, 2013, 317, 271-285. [51] W. Zhang, L. M. Wahl and P. Yu, Viral blips may not need a trigger: How transient viremia can arise in deterministic in-host models, SIAM Review, 2014, 56, 127-155. doi: 10.1137/130937421 [52] H. Zhu and X. Zou, Dynamics of a HIV-1 infection model with cell-mediated immune response and intracellular delay, Disc. Cont. Dyn. Syst. Ser. B., 2009, 12, 511-524. doi: 10.3934/dcdsb.2009.12.511 -
-
Figures(5) / Tables(5)
Export File
Citation
Shaoli Wang, Fei Xu. Analysis of an HIV model with post-treatment control[J]. Journal of Applied Analysis & Computation, 2020, 10(2): 667-685. doi: 10.11948/20190081
Format
Content
DownLoad:
-
Figure 1. Partial rank correlation coefficients for
$ R_0 $ and the frequency distribution of$ R_0. $ The parameters are shown in Table 5 -
Figure 2. Bistability and saddle-node bifurcation diagram of system (1.1). Here
$ c = 0.2914 $ is a saddle-node bifurcation (SN) point. The bistable interval is$ (0.2914, 0.4988). $ The parameter values are shown in Table 5. There are three phases in this figure. In phase I ($ 0<c<c_{2} $ ), the system has virus rebound. In phase II ($ c_{2}<c<c^{**} $ ), the system has bistable behavior. In phase Ⅲ ($ c>c^{**} $ ), the system is under elite control -
Figure 3. Time history of system (1.1) for
$ c = 0.45 $ ($ c_{2}<c<c^{**}). $ All the other parameter values are listed in Table 5. The trajectories of system (1.1) converge to different equilibria for different initial values, i.e., system (1.1) has bistable behavior. The initial values are$ x(0) = 600 $ ,$ L(0) = 13 $ ,$ y(0) = 20 $ ,$ z(0) = 1 $ (blue) and$ x(0) = 600 $ ,$ L(0) = 13 $ ,$ y(0) = 20 $ ,$ z(0) = 20 $ (red) -
Figure 4. Partial rank correlation coefficients for
$ c^{**} $ . The parameter values are shown in Table 5 -
Figure 5. Time history of system (5.1). The trajectories of system (5.1) converge to different equilibria for different initial values, i.e., system (5.1) has bistable behavior. The initial values are
$ x(0) = 600 $ ,$ L(0) = 13 $ ,$ y(0) = 20 $ ,$ z(0) = 1 $ (blue) and$ x(0) = 600 $ ,$ L(0) = 13 $ ,$ y(0) = 20 $ ,$ z(0) = 20 $ (red). The parameter values are shown in Table 5