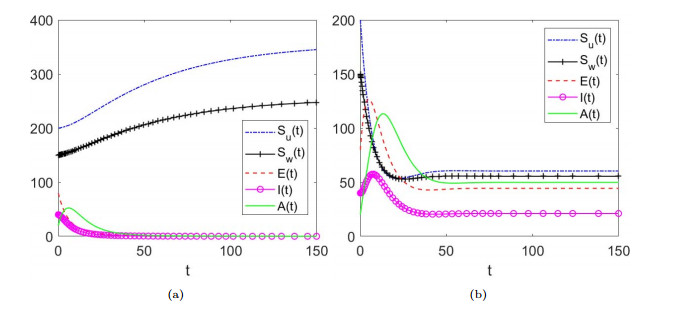
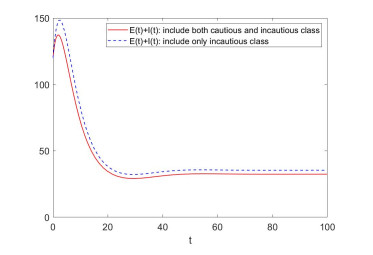
|
[1]
|
V. Capasso and G. Serio, A generalization of the Kermack-McKendrick deterministic epidemic model, Mathematical Biosciences, 1978, 42(1), 43–61.
Google Scholar
|
|
[2]
|
H. de Arazoza and R. Lounes, A nonlinear model for a sexually transmitted disease with contact tracing, Mathematical Medicine and Biology: A Journal of the IMA, 2002, 19(3), 221–234. doi: 10.1093/imammb/19.3.221
CrossRef Google Scholar
|
|
[3]
|
O. Diekmann, J. Heesterbeek and J. Metz, On the definition and the computation of the basic reproduction ratio $R_0$ in models for infectious diseases in heterogeneous populations, Journal of Mathematical Biology, 1990, 28(4), 365–382.
Google Scholar
|
|
[4]
|
P. Georgescu and Y. Hsieh, Global stability for a virus dynamics model with nonlinear incidence of infection and removal, SIAM Journal on Applied Mathematics, 2007, 67(2), 337–353.
Google Scholar
|
|
[5]
|
H. Hethcote, M. Lewis and P. van den Driessche, An epidemiological model with a delay and a nonlinear incidence rate, Journal of Mathematical Biology, 1989, 27(1), 49–64. doi: 10.1007/BF00276080
CrossRef Google Scholar
|
|
[6]
|
H. Hethcote and P. van den Driessche, Some epidemiological models with nonlinear incidence, Journal of Mathematical Biology, 1991, 29(3), 271–287. doi: 10.1007/BF00160539
CrossRef Google Scholar
|
|
[7]
|
W. Huang, M. Han and K. Liu, Dynamics of an SIS reaction-diffusion epidemic model for disease transmission, Mathematical Biosciences and Engineering, 2010, 7(1), 51–66.
Google Scholar
|
|
[8]
|
H. Huo and L. Feng, Global stability for an HIV/AIDS epidemic model with different latent stages and treatment, Applied Mathematical Modelling, 2013, 37(3), 1480–1489.
Google Scholar
|
|
[9]
|
J. Jia and G. Qin, Stability analysis of HIV/AIDS epidemic model with nonlinear incidence and treatment, Advances in Difference Equations, 2017, 2017(1), 136.
Google Scholar
|
|
[10]
|
W. Kermack and A. McKendrick, A contribution to the mathematical theory of epidemics, Proceedings of the Royal Society of London. Series A, 1927, 115(772), 700–721. doi: 10.1098/rspa.1927.0118
CrossRef Google Scholar
|
|
[11]
|
A. Korobeinikov and P. Maini, Non-linear incidence and stability of infectious disease models, Mathematical Medicine and Biology: A Journal of the IMA, 2005, 22(2), 113–128. doi: 10.1093/imammb/dqi001
CrossRef Google Scholar
|
|
[12]
|
J. Levy, Pathogenesis of human immunodeficiency virus infection, Microbiological Reviews, 1994, 46(2), 113.
Google Scholar
|
|
[13]
|
J. Li, Y. Yang, Y. Xiao and S. Liu, A class of Lyapunov functions and the global stability of some epidemic models with nonlinear incidence, Journal of Applied Analysis and Computation, 2016, 6(1), 38–46.
Google Scholar
|
|
[14]
|
A. Liapunov, Stability of motion, Elsevier, 2016.
Google Scholar
|
|
[15]
|
W. Liu, S. Levin and Y. Iwasa, Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models, Journal of Mathematical Biology, 1986, 23(2), 187–204. doi: 10.1007/BF00276956
CrossRef Google Scholar
|
|
[16]
|
Z. Ma and J. Li, Dynamical modeling and analysis of epidemics, International Association of Geodesy Symposia, 2009, 106(B11), xiv+498.
Google Scholar
|
|
[17]
|
R. Naresh, A. Tripathi and S. Omar, Modelling the spread of AIDS epidemic with vertical transmission, Applied Mathematics and Computation, 2006, 178(2), 262–272.
Google Scholar
|
|
[18]
|
S. Ruan and W. Wang, Dynamical behavior of an epidemic model with a nonlinear incidence rate, Journal of Differential Equations, 2003, 188(1), 135–163. doi: 10.1016/S0022-0396(02)00089-X
CrossRef Google Scholar
|
|
[19]
|
C. Silva and D. Torres, Global stability for a HIV/AIDS model, arXiv preprint arXiv: 1704.05806, 2017.
Google Scholar
|
|
[20]
|
L. Simpson and G. A., Mathematical assessment of the role of pre-exposure prophylaxis on HIV transmission dynamics, Applied Mathematics and Computation, 2017, 293, 168–193.
Google Scholar
|
|
[21]
|
B. Sounvoravong and S. Guo, Dynamics of a diffusive SIR epidemic model with time delay, Journal of Nonlinear Modeling and Analysis, 2019, 1(3), 319–334.
Google Scholar
|
|
[22]
|
G. Statistics, HIV BASICS: Overview: Data & Trend. HIV gov., 2018. https://www.hiv.gov/hiv-basics/overview/data-and-trends/global-statistics.
Google Scholar
|
|
[23]
|
C. Sun, J. Arino and S. Portet, Intermediate filament dynamics: Disassembly regulation, International Journal of Biomathematics, 2017, 10(1), 1750015 (22 pages). doi: 10.1142/S1793524517500152
CrossRef Google Scholar
|
|
[24]
|
C. Sun, Y. Hsieh and G. P., A model for HIV transmission with two interacting high-risk groups, Nonlinear Analysis: Real World Applications, 2018, 40, 170–184.
Google Scholar
|
|
[25]
|
P. van den Driessche and J. Watmough, A simple SIS epidemic model with a backward bifurcation, Journal of Mathematical Biology, 2000, 40(6), 525–540. doi: 10.1007/s002850000032
CrossRef Google Scholar
|
|
[26]
|
P. van den Driessche and J. Watmough, Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission, Mathematical Biosciences, 2002, 180(1), 29–48
Google Scholar
|
|
[27]
|
R. Weiss, How does HIV cause AIDS?, Science, 1993, 260(5112), 1273–1279. doi: 10.1126/science.8493571
CrossRef Google Scholar
|
|
[28]
|
W. Yang, Z. Shu, J. Lam and C. Sun, Global dynamics of an HIV model incorporating senior male clients, Applied Mathematics and Computation, 2017, 311, 203–216. doi: 10.1016/j.amc.2017.05.030
CrossRef Google Scholar
|
|
[29]
|
Z. Yuan and L. Wang, Global stability of epidemiological models with group mixing and nonlinear incidence rates, Nonlinear Analysis: Real World Applications, 2010, 11(2), 995–1004. doi: 10.1016/j.nonrwa.2009.01.040
CrossRef Google Scholar
|
|
[30]
|
T. Yusuf and F. Benyah, Optimal strategy for controlling the spread of HIV/AIDS disease: a case study of South Africa, Journal of Biological Dynamics, 2012, 6(2), 475–494. doi: 10.1080/17513758.2011.628700
CrossRef Google Scholar
|




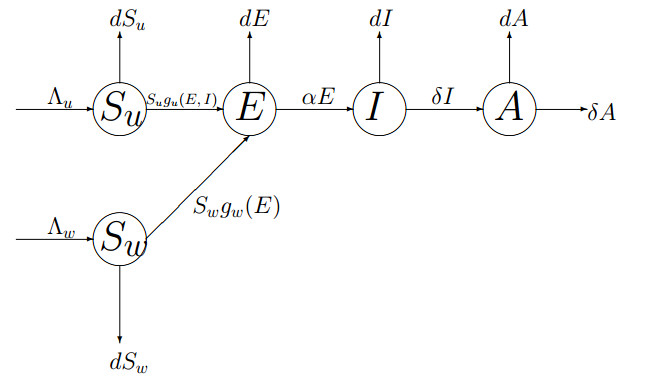

 DownLoad:
DownLoad: