| Citation: |
Xizhuang Xie, Jinsen Zhuang. BISTABILITY OF A TWO-SPECIES GILPIN-AYALA COMPETITION MODEL WITH STAGE STRUCTURE[J]. Journal of Applied Analysis & Computation, 2021, 11(2): 674-689. doi: 10.11948/20190219
|
BISTABILITY OF A TWO-SPECIES GILPIN-AYALA COMPETITION MODEL WITH STAGE STRUCTURE
-
Abstract
The dynamic behavior of bistability is considered for a two-species Gilpin-Ayala competition model with stage structure. By the theory of generalized saddle-point behavior for monotone semiflows, it is shown that there admits an invariant and $ K $-unordered $ C^1 $-separatrix, which separates the basins of attraction of the two locally stable single-species steady states. This implies that bistability occurs for two species. When two delays vary in their existence regions, we prove that the stability switching of the positive equilibria does not arise. By comparing with classical two-species Gilpin-Ayala competition model, we find that the introduction of stage structure brings negative effect on permanence of one species, but positive effect on its competitor. Finally, some numerical examples are given to illustrate the effectiveness of our theoretical results.
-
Keywords:
- Gilpin-Ayala /
- bistability /
- competition /
- stage structure /
- monotone semiflow
-
-
References
[1] W. G. Alello and H. I. Freedman, A time-delay model of single species growth with stage structure, Math. Biosci., 1990, 101, 139–153. doi: 10.1016/0025-5564(90)90019-U [2] Q. An, E. Beretta, Y. Kuang, C. Wang and H. Wang, Geometric stability switch criteria in delay differential equations with two delays and delay dependent parameters, J. Diff. Eqs., 2019, 266, 7073–7100. doi: 10.1016/j.jde.2018.11.025 [3] E. Beretta and Y. Kuang, Geometric stability switch criteria in delay differential systems with delay dependent parameters, SIAM J. Math. Anal., 2002, 33(5), 1144–1165. doi: 10.1137/S0036141000376086 [4] X. Chang, J. Shi and J. Zhang, Dynamics of a scalar population model with delayed Allee effect, Int. J. Bifurcat. Chaos, 2018, 28(12), 1850153. doi: 10.1142/S0218127418501535 [5] K. Deimling, Nonlinear Functional Analysis, Springer, Berlin, 1988. [6] C. Ferris and A. Best, The evolution of host defence to parasitism in fluctuating environments, J. Theor. Biol., 2017, 440, 58–65. [7] M. Gilpin and F. Ayala, Global models of growth and competition, Proc. Nat. Acad. Sci. USA, 1973, 70, 3590-3593. doi: 10.1073/pnas.70.12.3590 [8] M. Gilpin and F. Ayala, Schoener's model and Drosophila competition, Theor. Popul. Biol., 1976, 9, 12–14. doi: 10.1016/0040-5809(76)90031-9 [9] B. S. Goh and T. T. Agnew, Stability in Gilpin and Ayala's Models of Competition Nedlands, J. Math. Biol., 1997, 4, 275–279. [10] K. Gu, S. Niculescu and J. Chen, On stability crossing curves for general systems with two delays, J. Math. Anal. Appl., 2005, 311(1), 231–253. doi: 10.1016/j.jmaa.2005.02.034 [11] M. Iida, T. Muramatsu, H. Ninomiya and E. Yanagida, Diffusion-induced extinction of a superior species in a competition system, Japan J. Indust. Appl. Math., 1998, 15, 233–252. doi: 10.1007/BF03167402 [12] J. Jiang, X. Liang and X. Zhao, Saddle-point behavior for monotone semiflows and reaction-diffusion models, J. Diff. Eqs., 2004, 203, 313–330. doi: 10.1016/j.jde.2004.05.002 [13] Y. Kuang, Delay differential equations with applications in population biology, Mathematics in Science and Engineering, Academic Press, 1993, 191. [14] X. Liao and J. Li, Stability in Gilpin-Ayala competition models with diffusion, Nonlinear Anal-Theor., 1997, 28(10), 1751–1758. doi: 10.1016/0362-546X(95)00242-N [15] S. Liu and E. Beretta, Stage-structured Predator-prey model with the Beddington-DeAngelis functional response, SIAM J. Appl. Math., 2006, 66, 1101–1129. doi: 10.1137/050630003 [16] S. Liu, X. Xie and J. Tang, Competing population model with nonlinear intraspecfic regulation and maturation delays, Int. J. Biomath., 2012, 5(3), 1260007: 1–22. doi: 10.1142/S1793524512600078 [17] B. Lian and S. Hu, Asymptotic behaviour of the stochastic Gilpin-Ayala competition models, J. Math. Anal. Appl., 2008, 339, 419–428. doi: 10.1016/j.jmaa.2007.06.058 [18] J. D. Murray, Mathematical Biology I: An Introduction, 3rd ed. Springer-Verlag, Berlin, 2002. [19] H. L. Smith and H. R. Thieme, Stable coexistence and Bi-stability for competitive systems on ordered banach spaces, J. Diff. Eqs., 2001, 176, 195–222. doi: 10.1006/jdeq.2001.3981 [20] H. L. Smith, Monotone Dynamical Systems-An Introduction to the Theory of Competitive and Cooperative Systems, American Mathematical Society, 1995. [21] A. Settati and A. Lahrouz, On stochastic Gilpin-Ayala population model with Markovian switching, Biosystems, 2015, 130, 17–27. doi: 10.1016/j.biosystems.2015.01.004 [22] H. Shu, X. Hu, L. Wang and J. Watmough, Delay induced stability switch, multitype bistability and chaos in an intraguild predation model, J. Math. Biol., 2015, 71, 1269–1298. doi: 10.1007/s00285-015-0857-4 [23] K. Wang and Y. Zhu, Asymptotic properties of a stochastic Gilpin-Ayala model under regime swithching, Nonlinear Anal-Hybri., 2019, 32, 79–90. doi: 10.1016/j.nahs.2018.10.011 [24] S. Wang, F. Xu and L. Rong, Bistability analysis of an HIV model with immune response, J. Biol. Syst., 2017, 25(4), 677–695. doi: 10.1142/S021833901740006X -
-
Figures(9)
Export File
Citation
Xizhuang Xie, Jinsen Zhuang. BISTABILITY OF A TWO-SPECIES GILPIN-AYALA COMPETITION MODEL WITH STAGE STRUCTURE[J]. Journal of Applied Analysis & Computation, 2021, 11(2): 674-689. doi: 10.11948/20190219
Format
Content
DownLoad:
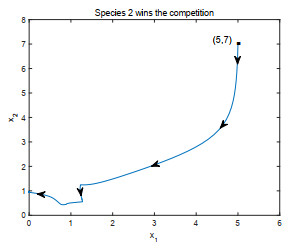
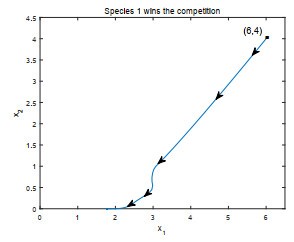
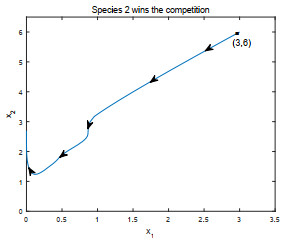
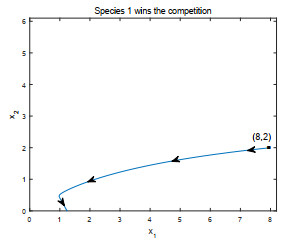
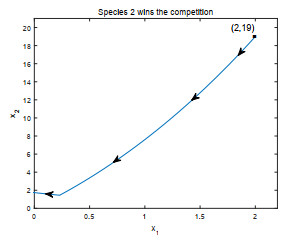
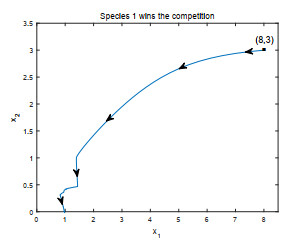
- Figure 1.
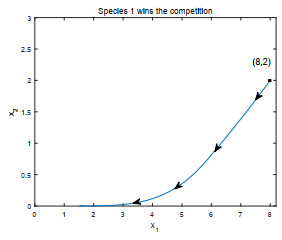
- Figure 2.
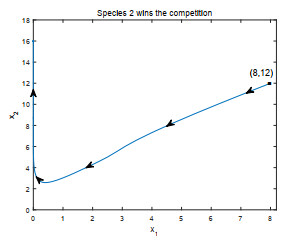
- Figure 3.
- Figure 4.
- Figure 5.
- Figure 6.
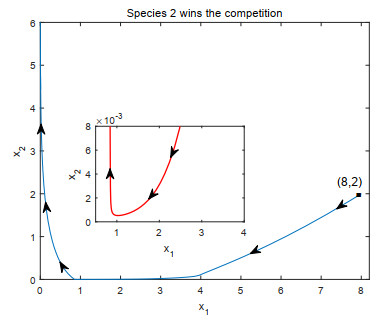
- Figure 7. The small graph is a detail view when x1 ∈ [0.5, 4].
- Figure 8.
- Figure 9.