| Citation: | Tiancai Liao, Hengguo Yu, Chuanjun Dai, Min Zhao. IMPACT OF NOISE IN A PHYTOPLANKTON-ZOOPLANKTON SYSTEM[J]. Journal of Applied Analysis & Computation, 2020, 10(5): 1878-1896. doi: 10.11948/20190272 |
IMPACT OF NOISE IN A PHYTOPLANKTON-ZOOPLANKTON SYSTEM
-
Abstract
In this paper, we investigate the dynamics of a delayed toxic phytoplankton-two zooplankton system incorporating the effects of L$ \acute{e} $vy noise and white noise. The value of this study lies in two aspects: Mathematically, we first prove the existence of a unique global positive solution of the system, and then we investigate the sufficient conditions that guarantee the stochastic extinction and persistence in the mean of each population. Ecologically, via numerical simulations, we find that the effect of white noise or L$ \acute{e} $vy noise on the stochastic extinction and persistence of phytoplankton and zooplankton are similar, but the synergistic effects of the two noises on the stochastic extinction and persistence of these plankton are stronger than that of single noise. In addition, an increase in the toxin liberation rate or the intraspecific competition rate of zooplankton was found to be capable to increase the biomass of the phytoplankton but decrease the biomass of zooplankton. These results may help us to better understand the phytoplankton-zooplankton dynamics in the fluctuating environments.-
Keywords:
- Noise /
- phytoplankton /
- zooplankton /
- extinction /
- persistence
-

-
References
[1] L. Bai, J. Li, K. Zhang and W. Zhao, Analysis of ratio-dependent predator-prey model driven by l$\acute{e}$vy noise, Appl. Math. Comput., 2014, 233, 480-493. [2] M. Bandyopadhyay, T. Saha and R. Pal, Determinstic and stochastic analysis of a delayed allelopathic phytoplankton model within fluctuating environment, Nolinear Anal-Hybri., 2008, 2, 958-970. doi: 10.1016/j.nahs.2008.04.001 [3] J. Bao, X. Mao, G. Yin and C. Yuan, Competitive lotka-volterra population dynamics with jumps, Nonlinear Anal., 2011, 74, 6601-6616. doi: 10.1016/j.na.2011.06.043 [4] Y. Cai, J. Jiao, Z. Gui et al., Environmental variability in a stochastic epidemic model, Appl. Math. Comput., 2018, 329, 210-226. [5] Y. Cai, Y. Kang and W. Wang, A stochastic sirs epidemic model with nonlinear incidence rate, Appl. Math. Comput., 2017, 305, 221-240. [6] Y. Cai, Y.Kang, M. Banerjee and W. Wang, A stochastic sirs epidemic model with infectious force under intervention strategies, J. Diff. Equ., 2015, 259, 7463-7502. doi: 10.1016/j.jde.2015.08.024 [7] Y. Cai, Z. Gui, X. Zhang et al., Bifurcations and pattern formation in a predator-prey model, Int. J. Bifurcat. Chaos, 2018, 28, 1850140. doi: 10.1142/S0218127418501407 [8] R. Chaudhuri, S. Roy and J. Chattopadhayay, Phytoplankton-zooplankton dynamics in the 'presence' or 'absence' of toxic phytoplankton, App. Math. Comput., 2013, 225, 102-116. doi: 10.1016/j.amc.2013.08.082 [9] C. Chen and Y. Kang, Dynamics of a stochastic multi-strain sis epidemic model driven by l$\acute{e}$vy noise, Commun. Nonlinear Sci. Numer. Simulat., 2017, 42, 379-395. doi: 10.1016/j.cnsns.2016.06.012 CrossRef $\acute{e}$vy noise" target="_blank">Google Scholar
[10] P. Classerman, Monte Carlo Methods in Financial Engineering, Springer-Verlag, Columbia University. [11] D. Conley, E. Bonsdorff, J. Carstensen et al., Tackling hypoxia in the baltic sea: Is engineering a solution?, Environ. Sci. Technol., 2009, 43, 3407-3411. doi: 10.1021/es8027633 [12] C. Dai, H. Yu and M. Zhao, Dynamics induced by delay in a nutrient-phytoplankton model with diffusion, Ecol. Complex., 2016, 26, 29-36. doi: 10.1016/j.ecocom.2016.03.001 [13] C. Dai, M. Zhao, H. Yu and Y. Wang, Delay-induced instability in a nutrient-phytoplankton system with flow, Phys. Rev. E, 2015, 91(3), 1-6. [14] S. Ding, M. Chen, M. Gong et al., Internal phosphorus loading from sediments causes seasonal nitrogen limitation for harmful algal blooms, Sci. Total. Environ., 2018, 625, 872-884. doi: 10.1016/j.scitotenv.2017.12.348 [15] W. K. Dodds, W. W. Bouska, J. L. Eitzmann et al., Eutrophication of u.s. freshwaters: analysis of potential economic damages, Environ. Sci. Technol., 2009, 43, 12-18. doi: 10.1021/es801217q [16] S. Gard, Persistence in stochastic food web models, Bull. Math. Biol., 1984, 46, 357-370. doi: 10.1016/S0092-8240(84)80044-0 [17] J. Geng, M. Liu and Y. Zhang, Stability of a stochastic one predator-two prey population model with time delays, Commun. Nonliear Sci. Numer. Simulat., 65-82, 53, 2017. [18] C. J. Gobler, O. M. Doherty, T. K. Hattenrath-Lehmann et al., Ocean warming since 1982 has expanded the niche of toxic algal blooms in the north atlantic and north pacific oceans, Pro. Natl. Acad. Sci. U. S. A., 4975-4980, 114, 2017. [19] K. Havens, T. Fukushima, P. Xie et al., Nutrient dynamics and the eutrophication of shallow lakes kasumigaura (japan), donghu (pr china), and okeechobee (usa), Environ. Pollut., 2001, 111, 263-272. doi: 10.1016/S0269-7491(00)00074-9 [20] S. Jang and E. Allen, Deterministic and stochastic nutrinet-phytoplankton-zooplankton models with periodic producing phytoplankton, Appl. Math. Comput., 2015, 271, 52-67. [21] T. Jang, J. Baglama and L. Wu, Dynamics of phytoplankton-zooplankton systems with toxin producing phytoplankton, Appl. Math. Comput., 2014, 227, 717-740. [22] J. Li, Y. Song, H. Wan and H. Zhu, Dynamics nanlysis a toxin-producing phytoplankton-zooplankton model with refuge, Math. Biosci. Eng., 2017, 14, 529-557. [23] R. Lipster, A strong law of large numbers for local martingales, Stochastic, 1980, 3, 217-228. doi: 10.1080/17442508008833146 [24] C. Liu, L. Wan, Q. Zhang and Y. Yan, Dynamical analysis in a bioeconamic phytoplankton-zooplankton system with double time delays and environmental stochasticity, Physical A, 2017, 482, 682-698. doi: 10.1016/j.physa.2017.04.104 [25] M. Liu and C. Bai, Dynamics of a stochastic one-prey two-predator model with l$\acute{e}$vy jump, Appl. Math. Comput., 2016, 284, 308-321. [26] M. Liu, C. Bai, M. Deng and B. Du, Analysis of stochastic two-prey one-predator model with l$\acute{e}$vy jumps, Physica A, 2016, 445, 176-188. doi: 10.1016/j.physa.2015.10.066 CrossRef $\acute{e}$vy jumps" target="_blank">Google Scholar
[27] M. Liu and K. Wang, Stochastic lotka-volterra systems with l$\acute{e}$vy noise, J. Math. Anal. Appl., 2014, 410, 750-763. doi: 10.1016/j.jmaa.2013.07.078 CrossRef $\acute{e}$vy noise" target="_blank">Google Scholar
[28] Q. Liu, Q. Chen and Z. Liu, Analysis on stochastic delay lotka-volterra systems driven by l$\acute{e}$vy noise, Appl. Math. Comput., 2014, 235, 261-271. [29] Q. Liu, D. Jiang, T. Hayat and A. Alsaedi, Dynamical behavior of a stochastic epidemic model for cholera, J. Franklin Inst., 2019, 356, 7486-7514. doi: 10.1016/j.jfranklin.2018.11.056 [30] Q. Liu, D. Jiang, T. Hayat and B. Ahmad, Stationary distribution and extinction of a stochastic predator-prey model with additional food and nonlinear perturbation, Appl. Math. Comput., 2018, 320, 226-239. [31] Q. Liu, D. Jiang, N. Shi et al., Dynamics of a stochastic delayed sir epidemic model with vaccination and double diseases driven by l$\acute{e}$vy jumps, Physica A, 2018, 492, 2010-2018. doi: 10.1016/j.physa.2017.11.116 CrossRef $\acute{e}$vy jumps" target="_blank">Google Scholar
[32] J. Lv and K. Wang, Asymptotic properties of a stochastic predator-prey system with holling ii functional response, Commun. Nonlinear Sci. Numer. Simulat., 2011, 16, 4037-4048. doi: 10.1016/j.cnsns.2011.01.015 [33] Y. Lv, J. Cao, J. Song et al., Global stability and hopf-bifurcation in a zooplankton-phytoplankton model, Nonlinear Dyn., 2014, 76, 345-366. doi: 10.1007/s11071-013-1130-2 [34] Z. Ma, M. Wu, L. Lin et al., Allelopathic interactions between the macroalga hizikia fusiformis (harvey) and the harmful blooms-forming dinoflagellate karenia mikimotoi, Harmful Algae, 2017, 65, 19-26. doi: 10.1016/j.hal.2017.04.003 [35] Q. Mandal, L. Allen and M. Banerjeer, Stochastic modellig of phytoplankton allelopathy, Appl. Math. Model., 2014, 138, 1583-1596. [36] X. Mao, Stochastic Differential Equations and Applications, Horwood Publishing, Chichaster, 1997. [37] X. Mao, G. Marion and E. Renshaw, Environmental noise suppresses explosion in population dynamics, Stoch. Process Appl., 2002, 97, 95-110. doi: 10.1016/S0304-4149(01)00126-0 [38] X. Mao and C. Yuan, Stochastic Differential Equations with Markovian Switching, Imperial College Press, 2006. [39] R. May, Stability and Complexity in Model Ecosystem, Princeton University Press, Princeton, 2001. [40] H. Paerl and J. Huisman, Blooms like it hot, Science, 2008, 320, 57-58. doi: 10.1126/science.1155398 [41] B. Qin, G. Zhu, G. Gao et al., A drinking water crisis in lake taihu, china: Linkage to climatic variability and lake management, Environ. Manage., 2010, 45, 105-112. doi: 10.1007/s00267-009-9393-6 [42] T. Saha and M. Bandyopadhyay, Dynamics analysis of toxin producing phytoplankton-zooplankton interactions, Nonlinear Anal. Real World Appl., 2009, 10, 314-332. doi: 10.1016/j.nonrwa.2007.09.001 [43] R. Shi and J. Yu, Hopf bifurcation analysis of two zooplankton-phytoplankton model with two delays, Chaos, Solitons and Fractals, 2017, 100, 62-73. doi: 10.1016/j.chaos.2017.04.044 [44] D. Valenti, G. Denaro, B. Spagnolo et al., Stochastic models for phytoplankton dynamics in mediterranean sea, Ecol.Comlex., 2016, 27, 84-103. doi: 10.1016/j.ecocom.2015.06.001 [45] J. Wang, Y. Cai, S. Fu and W. Wang, The effect of the fear factor on the dynamics of a predator-prey model incorporating the prey refuge, Chaos, 2019, 29, 083109. doi: 10.1063/1.5111121 [46] W. Wang, Y. Cai, Z. Ding and Z. Gui, A stochastic differential equation sis epidemic model incorporating ornstein-uhlenbeck process, Physica A, 2018, 509, 921-936. doi: 10.1016/j.physa.2018.06.099 [47] W. Wang, X. Gao, Y. Cai et al., Turing patterns in a diffusive epidemic model with saturated infection force, J. Franklin I., 2018, 355, 7226-7245. doi: 10.1016/j.jfranklin.2018.07.014 [48] Y. Wang, H. Wang and W. Jiang, Hopf-transcritical bifurcation in toixc producing phytoplankton-zooplankton model with delay, J. Math. Anal. Appl., 2014, 415, 574-594. doi: 10.1016/j.jmaa.2014.01.081 [49] R. Wu, X. Zhou and K. Wang, Dynamical behaviors of a competitive system under the influence of random disturbance and toxic substances, , Nonlinear Dyn., 2014, 77(4), 1209-1222. doi: 10.1007/s11071-014-1371-8 [50] B. Yang, Y. Cai, K. Wang and W. Wang, Global threshold dynamics of a stochastic epidemic model incorporating media coverage, Adv. Differ. Equ., 2018, 2018, 462. doi: 10.1186/s13662-018-1925-z [51] B. Yang, Y. Cai, K. Wang and W. Wang, Optimal harvesting policy of logistic population model in a randomly fluctuating environment, Physica A, 2019, 526, 120817. doi: 10.1016/j.physa.2019.04.053 [52] H. Yu, M. Zhao, Q. Wang and R. Agarwal, A focus on long-run sustainability of an impulsive switched eutrophication controlling system based upon the zeya reservoir, J. Franklin I., 2014, 351, 487-499. doi: 10.1016/j.jfranklin.2013.08.025 [53] X. Yu, S. Yuan and T. Zhang, The effects of toxin-producing phytoplankton and environmental fluctuations on the planktonic booms, Nonlinear Dyn., 2018, 91, 1653-1668. doi: 10.1007/s11071-017-3971-6 [54] H. Zhang, Y. Cai, S. Fu and W. Wang, Impact of the fear effect in a prey-predator model incorporating a prey refuge, Appl. Math. Comput., 2019, 356, 328-337. [55] X. Zhang and K. Wang, Stability analysis of a stochastic gilpin-ayala model driven by l$\acute{e}$vy noise, Commun. Nonlinear Sci. Numer. Simulat., 2014, 19, 1391-1399. doi: 10.1016/j.cnsns.2013.09.013 CrossRef $\acute{e}$vy noise" target="_blank">Google Scholar
[56] Y. Zhao and S. Yuan, Stability in distribution of a hybrid system competitive lotka-volterra model with l$\acute{e}$vy jumps, Chaos Soltions Fractals, 2016, 85, 98-109. doi: 10.1016/j.chaos.2016.01.015 CrossRef $\acute{e}$vy jumps" target="_blank">Google Scholar
[57] Z. Zhao and Q. Jiang, The threshold of a stochastic sis epidemic model with vaccination, Appl. Math. Comput., 2014, 243, 718-727. -
-
-
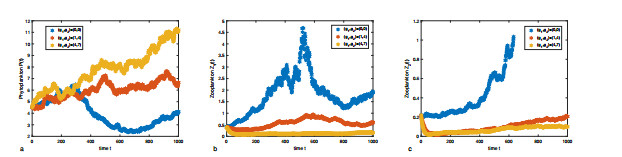
Figure 1. The solutions of stochastic system (1.2) with time step
$ \Delta t = 0.001 $ and different white noise intensities.a for$ (\delta_{1}, \delta_{2}, \delta_{3}, \delta_{4}, \delta_{5}) = (0.40, 0.41, 0.42, 0.43, 0.44) $ . b for$ (\delta_{1}, \delta_{2}, \delta_{3}, \delta_{4}, \delta_{5}) = (0.80, 0.81, 0.82, 0.83, 0.84) $ . c for$ (\delta_{1}, \delta_{2}, \delta_{3}, \delta_{4}, \delta_{5}) = (1.80, 1.81, 1.82, 1.83, 1.84) $ . -
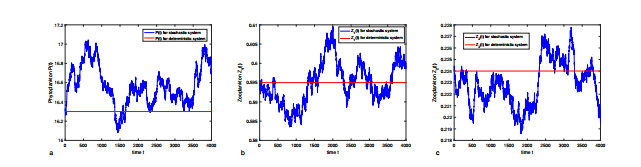
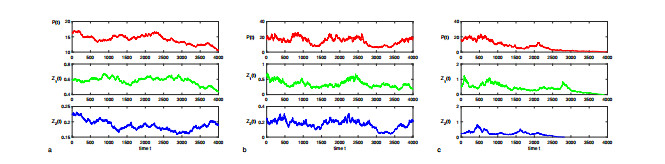
Figure 2. The solutions of stochastic system (1.2) and its deterministic system (1.1) with time step
$ \Delta t = 0.001 $ . a for phytoplankton$ P(t) $ . b for zooplankton$ Z_{1}(t) $ . c for zooplankton$ Z_{2}(t) $ . -
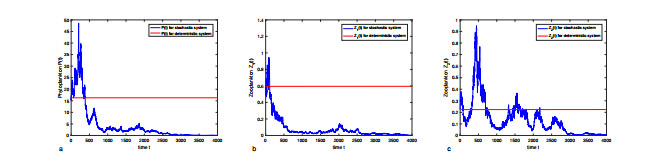
Figure 3. The solutions of the stochastic system (1.2) and its deterministic system (1.1) with time step
$ \Delta t = 0.001 $ . a for phytoplankton$ P(t) $ . b for zooplankton$ Z_{1}(t) $ . c for zooplankton$ Z_{2}(t) $ . -
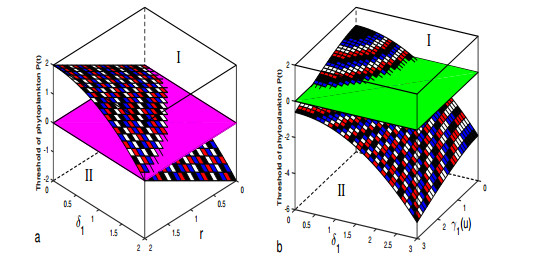
Figure 4. The sensitivity analysis of the threshold for phytoplankton
$ P(t) $ in system (1.2) with respect to its growth rate and noise intensities. a for$ r $ and$ \delta_{1} $ . b for$ \delta_{1} $ and$ \gamma_{1}(u) $ . The space region$ \rm{I} $ denotes the persistence of phytoplankton, the space region$ \rm{II} $ indicates the extinction of phytoplankton, and the planes (pink and green) represent the critical plane between the persistence and extinction of phytoplankton. -
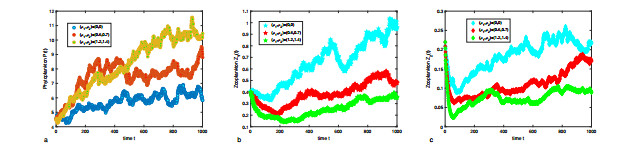
Figure 5. The effects of toxin liberation rate
$ \rho_{i} $ on the dynamics of plankton in the stochastic system (1.2). -
Figure 6. The effects of intraspecific coefficient
$ g_{i}(i = 1, 2) $ on the dynamics of plankton in the stochastic system (1.2).




 DownLoad:
DownLoad: