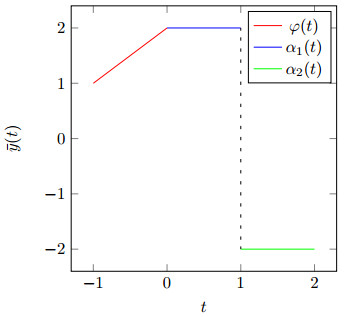
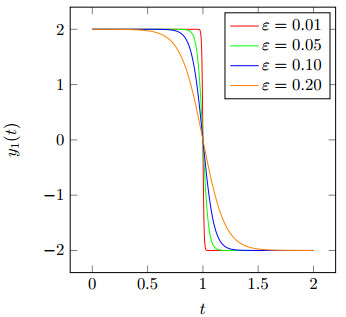
|
[1]
|
Z. Bartoszewski and A. Baranowska, Solving boundary value problems for second order singularly perturbed delay differential equations by 'ε'–approximate fixed–point method, Math. Model. Anal., 2015, 20(3), 369–381.
Google Scholar
|
|
[2]
|
Y. Cao, Bifurcations in an internet congestion control system with distributed delay, Appl. Math. Comput., 2019, 347, 54–63.
Google Scholar
|
|
[3]
|
È. Èl'sgol'c, Qualitative Methods in Mathematical Analysis, American Mathematical Society, Providence, 1964.
Google Scholar
|
|
[4]
|
F. Erdogan and Z. Cen, A uniformly almost second order convergent numerical method for singularly perturbed delay differential equations, J. Comput. Appl. Math., 2018, 333, 282–394.
Google Scholar
|
|
[5]
|
H. Gao, X. Meng and T. Chen, Stabilization of networked control systems with a new delay characterization, IEEE Trans. Automat. Control, 2008, 53(9), 2142–2148. doi: 10.1109/TAC.2008.930190
CrossRef Google Scholar
|
|
[6]
|
S. Hu and Q. Zhu, Stochastic optimal control and analysis of stability of networked control systems with long delay, Automatica, 2003, 39(11), 1877–1884. doi: 10.1016/S0005-1098(03)00196-1
CrossRef Google Scholar
|
|
[7]
|
H. Kargar, J. Zarei and R. Razavi–Far, Robust fault detection filter design for nonlinear networked control systems with time–varying delays and packet dropout, Circuits, Systems, Signal Process., 2019, 38(1), 63–84.
Google Scholar
|
|
[8]
|
Y. Kuang, Delay Differential Equations with Applications in Population Dynamics, Academic Press, Boston, 1993.
Google Scholar
|
|
[9]
|
C. Kuehn, Multiple Time Scale Dynamics, Applied Mathematical Sciences, Springer, 2015.
Google Scholar
|
|
[10]
|
C. Lange and R. Miura, Singular perturbation analysis of boundary–value problems for differential–difference equations. VI. small shifts with rapid oscillations, SIAM J. Appl. Math., 1994, 54(1), 273–283.
Google Scholar
|
|
[11]
|
M. Ni and W. Lin, The asymptotic solutions of delay singularly perturbed differential difference equations (in Chinese), Acta Math. Sci., 2010, 30A(6), 1413–1423. Available from: http://121.43.60.238/sxwlxbA/CN/Y2010/V30/I6/1413.
Google Scholar
|
|
[12]
|
M. Ni, On the internal layer for a singularly perturbed system of second–order delay differential equations, Diff. Equ., 2013, 49(8), 941–954. doi: 10.1134/S001226611308003X
CrossRef Google Scholar
|
|
[13]
|
N. Olgac, H. Elmali, M. Hosek and M. Renzulli, Active vibration control of distributed systems using delayed resonator with acceleration feedback, J. Dyn. Syst., Measure., Control, 1997, 119(3), 380–389. doi: 10.1115/1.2801269
CrossRef Google Scholar
|
|
[14]
|
V. Rožkov, On the asymptotic behaviour of solutions of equations of neutral type with small time lag (in Russian), Ž. Vyčisl. Mat. i Mat. Fiz., 1964, 4(4, suppl.), 161–175.
Google Scholar
|
|
[15]
|
V. Rožkov, Asymptotic formulae in terms of a small time lag for the solution of an equation of neutral type with two retarded arguments (in Russian), Ž. Vyčisl. Mat. i Mat. Fiz., 1964, 4(4, suppl.), 176–182.
Google Scholar
|
|
[16]
|
V. Rožkov, Equations of neutral types with variable small retardation (in Russian), Differencial'nye Uravnenija, 1966, 2, 407–416.
Google Scholar
|
|
[17]
|
V. Rožkov, An equation of neutral type with a small retardation dependent on the unknown function (in Russian), Izv. Vysš. Učebn. Zaved. Mat., 1968, 1968(6), 90–97.
Google Scholar
|
|
[18]
|
J. Ren and W. Ge, Singularly perturbed boundary value problems for semi–linear retarded differential equations with nonlinear boundary conditions, Appl. Math. Mech., 2003, 24(12), 1450–1455. doi: 10.1007/BF02435586
CrossRef Google Scholar
|
|
[19]
|
H. Tian, Asymptotic expansion for the solutions of singularly perturbed delay differential equations, J. Math. Anal. Appl., 2003, 281(2), 678–696.
Google Scholar
|
|
[20]
|
A. Vasil'eva, An equation of neutral type with small lag (in Russian), Dokl. Akad. Nauk SSSR, 1962, 145, 495–497.
Google Scholar
|
|
[21]
|
A. Vasil'eva and V. Butuzov, Asymptotic methods in the theory of singular perturbations (in Russian), Vyssh. Shkola, Moscow, 1990.
Google Scholar
|
|
[22]
|
V. Volterra, Fluctuations in the abundance of a species considered mathematically, Nature, 1926, 118(2972), 558–560. doi: 10.1038/118558a0
CrossRef Google Scholar
|
|
[23]
|
A. Wang and M. Ni, The interior layer for a nonlinear singularly perturbed differential–difference equation, Acta Math. Sci., 2012, 32B(2), 695–709.
Google Scholar
|
|
[24]
|
N. Wang and M. Ni, The interior layer phenomena for a class of singularly perturbed delay–differential equations, Acta Math. Sci., 2013, 33B(2), 532–542.
Google Scholar
|




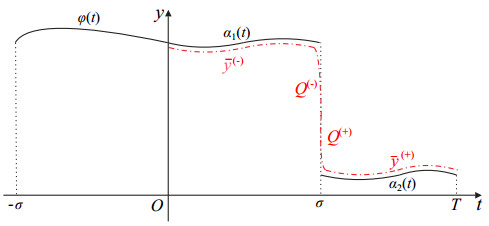

 DownLoad:
DownLoad: