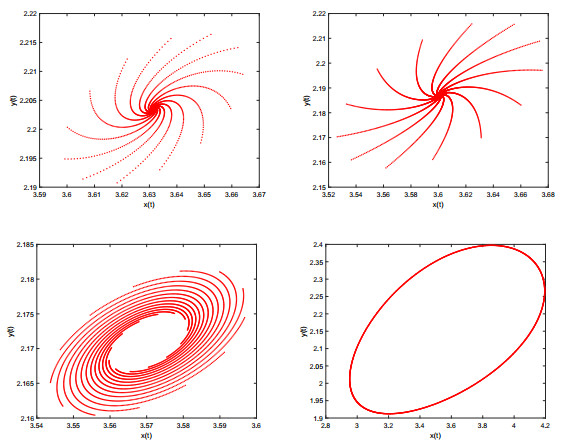
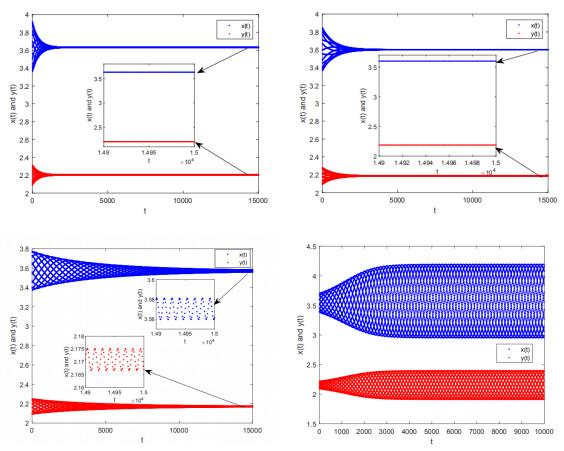
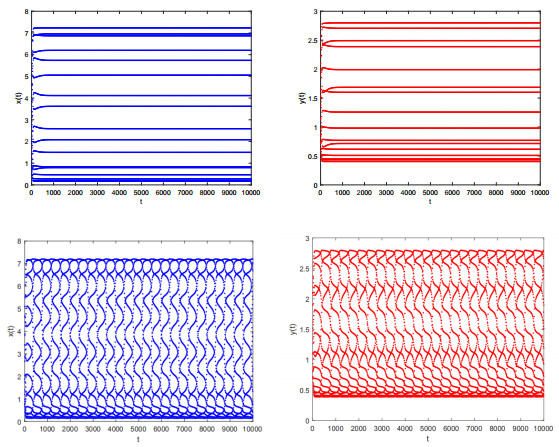
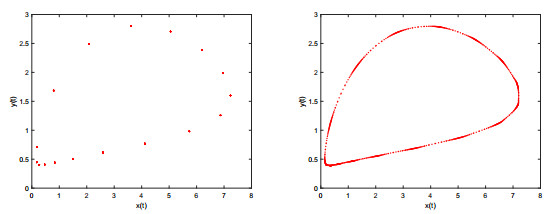
|
[1]
|
I. Ahn and C. Yoon, Global well-posedness and stability analysis of prey-predator model with indirect prey-taxis, Journal of Differential Equations, 2019.
Google Scholar
|
|
[2]
|
J. R. Beddington, C. A. Free and J. H. Lawton, Dynamic complexity in predator-prey models framed in diffrence equations, Nature, 1975, 255(5503), 58–60. doi: 10.1038/255058a0
CrossRef Google Scholar
|
|
[3]
|
Y. Bai and Y. Li, Stability and Hopf bifurcation for a stage-structured predator-prey model incorporating refuge for prey and additional food for predator, Advances in Difference Equations, 2019, 2019, 42. doi: 10.1186/s13662-019-1979-6
CrossRef Google Scholar
|
|
[4]
|
J. B. Collings, Bifurcation and stability analysis of a temperature-dependent mite predator-prey interaction model incorporating a prey refuge, Bulletin of mathematical biology, 1995, 57(1), 63–76.
Google Scholar
|
|
[5]
|
S. Creel and D. Christianson, Relationships between direct predation and risk effects, Trends in Ecology & Evolution, 2008, 23(4), 194-201.
Google Scholar
|
|
[6]
|
S. Creel, D. Christianson, S. Liley and J. A. Winnie, Predation risk affects reproductive physiology and demography of elk, Science, 2007, 315(5814), 960–960. doi: 10.1126/science.1135918
CrossRef Google Scholar
|
|
[7]
|
W. Cresswell, Predation in bird populations, Journal of Ornithology, 2011, 152(1), 251–263.
Google Scholar
|
|
[8]
|
F. Chen, L. Chen and X. Xie, On a Leslie-Gower predator-prey model incorporating a prey refuge, Nonlinear Analysis Real World Applications, 2009, 10(5), 2905–2908. doi: 10.1016/j.nonrwa.2008.09.009
CrossRef Google Scholar
|
|
[9]
|
Y. Cai, Z. Gui, X. Zhang, H. Shi and W. Wang, Bifurcations and pattern formation in a predator-prey model, International Journal of Bifurcation and Chaos, 2018, 28(11), 1850140. doi: 10.1142/S0218127418501407
CrossRef Google Scholar
|
|
[10]
|
Y. Cai and X. Mao, Stochastic prey-predator system with foraging arena scheme, Applied Mathematical Modelling, 2018, 64, 357–371. doi: 10.1016/j.apm.2018.07.034
CrossRef Google Scholar
|
|
[11]
|
A. Das and G. P. Samanta, A prey-predator model with refuge for prey and additional food for predator in a fluctuating environment, Physica A: Statistical Mechanics and its Applications, 2020, 538.
Google Scholar
|
|
[12]
|
C. P. Haight, Some observations on the predator-prey complex in the Gallatin valley, predatory animals environmental aspects montana gallatin valley, 1941.
Google Scholar
|
|
[13]
|
H. Huo and W. Li, Stable periodic solution of the discrete periodic Leslie-Gower predator-prey model, Mathematical and Computer Modelling, 2004, 40(3–4), 261–269.
Google Scholar
|
|
[14]
|
J. Huang, S. Liu, S. Ruan and D. Xiao, Bifurcations in a discrete predator-prey model with nonmonotonic functional response, Journal of Mathematical Analysis and Applications, 2018, 464(1), 201–230. doi: 10.1016/j.jmaa.2018.03.074
CrossRef Google Scholar
|
|
[15]
|
A. Irfan, S. Umer and D. Qamar, Bifurcation analysis and chaos control in discrete-time system of three competing species, Arabian Journal of Mathematics, 2019, 8(1), 1–14. doi: 10.1007/s40065-018-0207-7
CrossRef Google Scholar
|
|
[16]
|
M. Kot, Elements of mathematical ecology, Cambridge Univercity Press, Cambridge, 2001.
Google Scholar
|
|
[17]
|
Y. Kuznetsov, Elements of Applied Bifurcation Theory, Springer-Verlag, New York, 1998.
Google Scholar
|
|
[18]
|
T. K. Kar, Stability analysis of a prey-predator model incorporating a prey refuge, Communications in Nonlinear Science and Numerical Simulation, 2005, 10(6), 681–691. doi: 10.1016/j.cnsns.2003.08.006
CrossRef Google Scholar
|
|
[19]
|
A. Lotka, Elements of physical biology, reprinted 1956 as elements of mathematical biology, Williams & Wilkins company, 1924.
Google Scholar
|
|
[20]
|
P. H. Leslie, Some further notes on the use of matrices in population mathematics, Biometrika, 1948, 35(3–4), 213–245. doi: 10.1093/biomet/35.3-4.213
CrossRef Google Scholar
|
|
[21]
|
S. Lester Lynne, A predator-prey relationship between the short-eared owl and the meadow mouse, The Wilson Bulletin, 1938, 50(2), 110–112.
Google Scholar
|
|
[22]
|
S. L. Lima, Nonlethal effects in the ecology of predator-prey interactions, Bioscience, 1998, 48(1), 25–34.
Google Scholar
|
|
[23]
|
S. L. Lima, Predators and the breeding bird: behavioural and reproductive flexibility under the risk of predation, Biological reviews, 2009, 84(3), 485–513. doi: 10.1111/j.1469-185X.2009.00085.x
CrossRef Google Scholar
|
|
[24]
|
Y. Lv, Y. Pei and Y. Wang, Bifurcations and simulations of two predator-prey models with nonlinear harvesting, Chaos, Solitons and Fractals, 2019, 120, 158–170. doi: 10.1016/j.chaos.2018.12.038
CrossRef Google Scholar
|
|
[25]
|
A. J. Nicholson and V. A. Bailey, The balance of animal populations, Proceedings of the Zoological Society of London, 1935, 105(3), 551–598. doi: 10.1111/j.1096-3642.1935.tb01680.x
CrossRef Google Scholar
|
|
[26]
|
N. Pettorelli, T. Coulson, S. M. Durant and J. M. Gaillard, Predation, individual variability and vertebrate population dynamics, Oecologia, 2011, 167(2), 305–314. doi: 10.1007/s00442-011-2069-y
CrossRef Google Scholar
|
|
[27]
|
S. D. Peacor, B. L. Peckarsky, G. C. Trussell and J. R. Vonesh, Costs of predator-induced phenotypic plasticity: a graphical model for predicting the contribution of nonconsumptive and consumptive effects of predators on prey, Oecologia, 2013, 171(1), 1–10. doi: 10.1007/s00442-012-2394-9
CrossRef Google Scholar
|
|
[28]
|
E. L. Preisser, D. I. Bolnick and A. Hector, The many faces of fear: comparing the pathways and impacts of nonconsumptive predator effects on prey populations, PLoS One, 2008, 3(6), e2465. doi: 10.1371/journal.pone.0002465
CrossRef Google Scholar
|
|
[29]
|
J. Song, M. Hu, Y. Bai and Y. Xia, Dynamic analysis of a non-autonomous ratio-dependent predator-prey model with additional food, Journal of Applied Analysis and Computation, 2018, 8(6), 1893–1909.
Google Scholar
|
|
[30]
|
T. O. Svennungsen, H. Holen and O. Leimer, Inducible defenses: continuous reaction norms or threshold traits?, American Naturalist, 2011, 178(3), 397–410. doi: 10.1086/661250
CrossRef Google Scholar
|
|
[31]
|
V. Volterra, Variazionie fluttuazioni del Numero dยก'individui in specie animali conviventi, Mem. R. Accad. Naz. Lincei, 1926, 31–113.
Google Scholar
|
|
[32]
|
G. Wen, Criterion to identify hopf bifurcations in maps of arbitary dimension, Physical review E, 2005, 72(2), 026201. doi: 10.1103/PhysRevE.72.026201
CrossRef Google Scholar
|
|
[33]
|
X. Wang, L. Zanette and X. Zou, Modelling the fear effect in predator-prey interactions, Journal of mathematical biology, 2016, 73(5), 1179–1204. doi: 10.1007/s00285-016-0989-1
CrossRef Google Scholar
|
|
[34]
|
J. Wang, Y. Cai, S. Fu and W. Wang, The effect of the fear factor on the dynamics of a predator-prey model incorporating the prey refuge, Chaos: An Interdisciplinary Journal of Nonlinear Science, 2019, 29(8).
Google Scholar
|
|
[35]
|
S. Yao, New bifurcation critical criterion of Flip-Neimark-Sacker bifurcations for Tow-Parameterized family of n-dimensional discrete systems, Discrete Dynamics in Nature and Society, 2012, 2012, 1–12.
Google Scholar
|
|
[36]
|
Y. Zhou, W. Sun, Y. Song, Z. Zheng, J. Lu and S. Chen, Hopf bifurcation analysis of a predator-prey model with Holling-Ⅱ type functional response and a prey refuge, Nonlinear Dynamics, 2019, 97, 1–12. doi: 10.1007/s11071-019-04901-1
CrossRef Google Scholar
|
|
[37]
|
X. Zhao and Z. Zeng, Stationary distribution and extinction of a stochastic ratio-dependent predator-prey system with stage structure for the predator, Physica A: Statistical Mechanics and its Applications, 2019.
Google Scholar
|
|
[38]
|
L. Zhang, C. Zhang and Z. He, Codimension-one and codimension-two bifurcations of a discrete predator-prey system with strong Allee effect, Mathematics and Computers in Simulation, 2019, 162, 155–178. doi: 10.1016/j.matcom.2019.01.006
CrossRef Google Scholar
|
|
[39]
|
L. Y. Zanette, A. F. White, M. C. Allen and C. Michael, Perceived predation risk reduces the number of offspring songbirds produce per year, Science, 2011, 334(6061), 1398–1401. doi: 10.1126/science.1210908
CrossRef Google Scholar
|




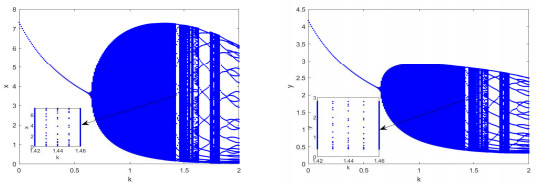

 DownLoad:
DownLoad: