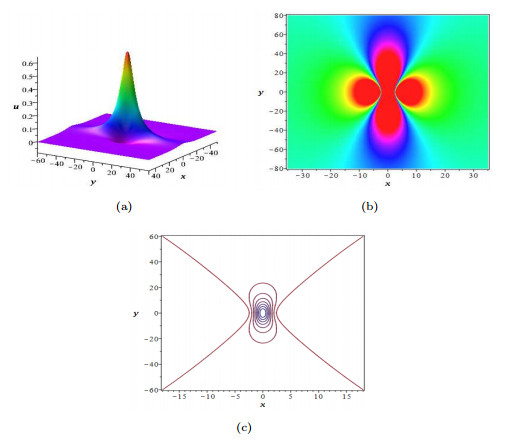
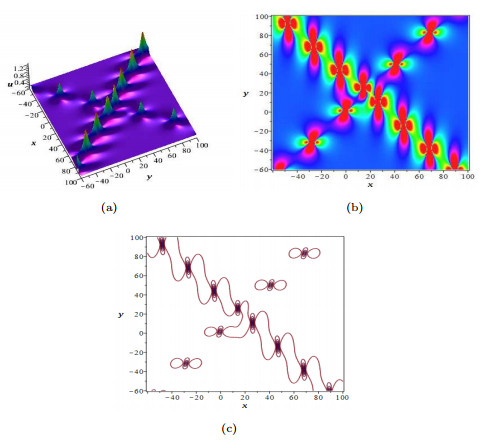
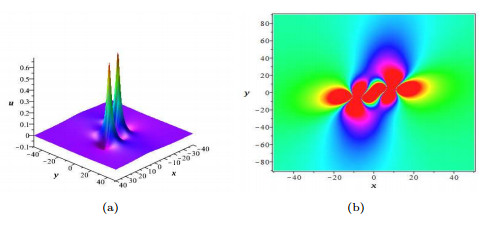
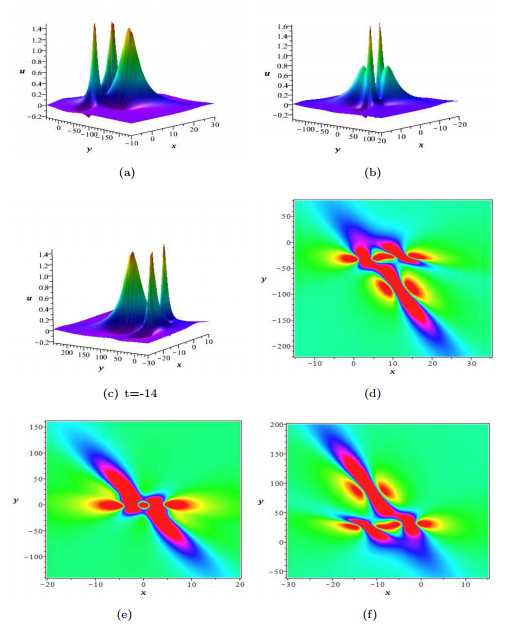
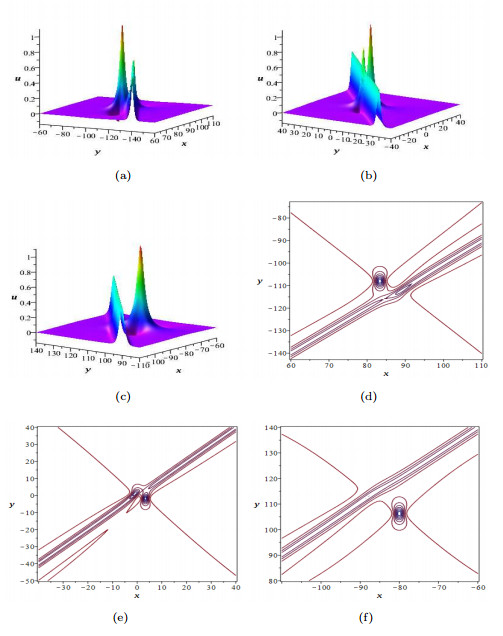
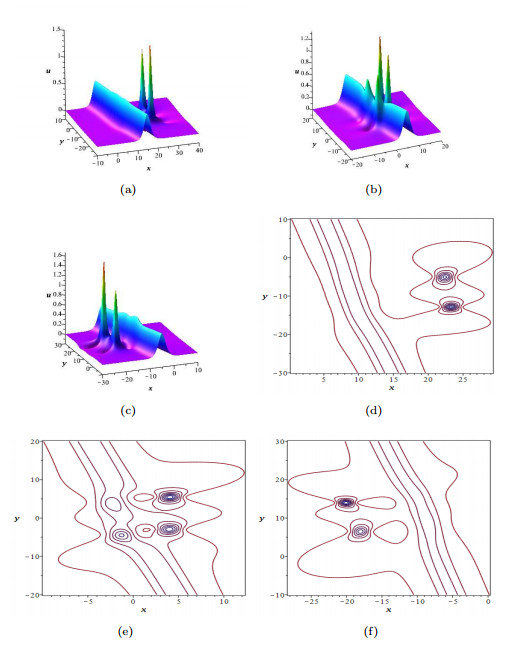
|
[1]
|
M. J. Ablowitz, M. A. Ablowitz and P. A. Clarkson, Solitons, nonlinear evolution equations and inverse scattering, Cambridge university press, 1991.
Google Scholar
|
|
[2]
|
M. Chen, X. Li, Y. Wang and B. Li, A Pair of Resonance Stripe Solitons and Lump Solutions to a Reduced ($3+1$)-dimensional Nonlinear Evolution Equation, Commun. Theor. Phys., 2017, 67, 595. doi: 10.1088/0253-6102/67/6/595
CrossRef Google Scholar
|
|
[3]
|
J. M. Dye and A. Parker, A bidirectional Kaup-Kupershmidt equation and directionally dependent solitons, J. Math. Phys., 2002, 43(10), 4921-4949. doi: 10.1063/1.1503866
CrossRef Google Scholar
|
|
[4]
|
E. Date, M. Jimbo, M. Kashiwara and T. Miwa, Transformation groups for soliton equations-Euclidean Lie algebras and reduction of the KP hierarchy, Publ. Res. Inst. Math. Sci., 1982, 18, 1077-1110. doi: 10.2977/prims/1195183297
CrossRef Google Scholar
|
|
[5]
|
L. Feng and T. Zhang, Breather wave, rogue wave and solitary wave solutions of a coupled nonlinear Schrödinger equation, Appl. Math. Lett., 2018, 78, 133-140. doi: 10.1016/j.aml.2017.11.011
CrossRef Google Scholar
|
|
[6]
|
C. Gu, H. Hu and Z. Zhou, Darboux transformation in soliton theory and its geometric applications, Shanghai. Sci. Tech. Publ. Shanghai, 1999, 1, 999.
Google Scholar
|
|
[7]
|
R. Hirota, The Direct Method in Soliton Theory, Cambridge University Press, New York(NY), 2004.
Google Scholar
|
|
[8]
|
M. Jimbo and T. Miwa, Solitons and infinite dimensional Lie algebras, Publ. Res. Inst. Math. Sci., 1983, 19, 943-1001. doi: 10.2977/prims/1195182017
CrossRef Google Scholar
|
|
[9]
|
P. G. Kevrekidis and D. J. Frantzeskakis, Solitons in coupled nonlinear models: a survey of recent developments, Rev. Phys., 2016, 1, 140-153. doi: 10.1016/j.revip.2016.07.002
CrossRef Google Scholar
|
|
[10]
|
Y. Liu, B. Li and H. An, General high-order breathers, lumps in the ($2+1$)-dimensional Boussinesq equation, Nonlinear Dyn., 2018, 92, 2061-2076. doi: 10.1007/s11071-018-4181-6
CrossRef Google Scholar
|
|
[11]
|
J. Lv and S. D. Bilige, Lump solutions of a ($2+1$)-dimensional bSK equation, Nonlinear Dyn., 2017, 90(3), 2119-2124. doi: 10.1007/s11071-017-3788-3
CrossRef Google Scholar
|
|
[12]
|
X. Lai and X. Cai, Adomian decomposition method for approximating the solutions of the bidirectional Sawada-Kotera Equation, Z. Naturf., 2010, 65a, 658-664.
Google Scholar
|
|
[13]
|
V. B. Matveev and M. A. Salle, Darboux transformations and solitons, Springer, Berlin, 1991.
Google Scholar
|
|
[14]
|
Y. Matsuno, Bilinear Transformation Method, Academic, New York(NY), 1984.
Google Scholar
|
|
[15]
|
H. Ma and A. Deng, Lump solution of ($2+1$)-dimensional Boussinesq equation, Commun. Theor. Phys., 2016, 65, 546. doi: 10.1088/0253-6102/65/5/546
CrossRef Google Scholar
|
|
[16]
|
W. Ma, Lump solutions to the Kadomtsev-Petviashvili equation, Phys. Lett. A, 2015, 379, 1975-1978. doi: 10.1016/j.physleta.2015.06.061
CrossRef Google Scholar
|
|
[17]
|
Y. Ma and X. Geng, Darboux and Bäcklund transformations of the bidirectional Sawada-Kotera equation, Appl. Math. Comput., 2012, 218(12), 6963-6965.
Google Scholar
|
|
[18]
|
W. Ma, X. Yong and H. Q, Diversity of interaction solutions to the ($2+1$)-dimensional Ito equation, Comput. Math. Appl., 2018, 75, 289-295. doi: 10.1016/j.camwa.2017.09.013
CrossRef Google Scholar
|
|
[19]
|
W. Peng, S. Tian and T. Zhang, Breather waves, high-order rogue waves and their dynamics in the coupled nonlinear Schrödinger equations with alternate signs of nonlinearities, EPL, 2019. DOI: 10.1209/0295-5075/127/50005.
CrossRef Google Scholar
|
|
[20]
|
W. Peng and S. Tian, Dynamics of breather waves and higher-order rogue waves in a coupled nonlinear Schrödinger equation, EPL (Europhysics Letters), 2018. DOI: 10.1209/0295-5075/123/50005.
CrossRef Google Scholar
|
|
[21]
|
H. Sun and A. Chen, Lump and lump-kink solutions of the ($3+1$)-dimensional Jimbo-Miwa and two extended Jimbo-Miwa equations, Appl. Math. Lett., 2017, 68, 55-61. doi: 10.1016/j.aml.2016.12.008
CrossRef Google Scholar
|
|
[22]
|
A. M. Wazwaz, The generalized Kaup-Boussinesq equation: multiple soliton solutions, Waves. Random. Complex. Media., 2015, 25, 473-481. doi: 10.1080/17455030.2015.1016474
CrossRef Google Scholar
|
|
[23]
|
H. Wang, Lump and interaction solutions to the ($2+1$)-dimensional Burgers equation, Appl. Math. Lett., 2018, 85, 27-34. doi: 10.1016/j.aml.2018.05.010
CrossRef Google Scholar
|
|
[24]
|
Y. Wang, M. Chen, X. Li and B. Li, Some interaction solutions of a reduced generalised ($3+1$)-dimensional shallow water wave equation for lump solutions and a pair of resonance solitons, Z. Naturf. A, 2017, 72, 419-424. doi: 10.1515/zna-2017-0057
CrossRef Google Scholar
|
|
[25]
|
X. Yan, S. Tian, M. Dong, and T. Zhang, Rogue Waves and Their Dynamics on Bright-Dark Soliton Background of the Coupled Higher Order Nonlinear Schrödinger Equation, J. Phys. Soc. Japan, 2019. DOI: 10.7566/JPSJ.88.074004.
CrossRef Google Scholar
|
|
[26]
|
J. Yu and Y. Sun, Study of lump solutions to dimensionally reduced generalized KP equations, Nonlinear Dyn., 2017, 87, 2755-2763. doi: 10.1007/s11071-016-3225-z
CrossRef Google Scholar
|
|
[27]
|
J. Yang and W. Ma, Lump solutions to the BKP equation by symbolic computation, Int. J. Mod. Phys. B, 2016, 30, 1640028. doi: 10.1142/S0217979216400282
CrossRef Google Scholar
|
|
[28]
|
J. Yang, W. Ma and Z. Qin, Lump and lump-soliton solutions to the ($2+1$)-dimensional Ito equation, Anal. Math. Phys., 2018, 8, 427-436. doi: 10.1007/s13324-017-0181-9
CrossRef Google Scholar
|
|
[29]
|
H. Zhang and W. Ma, Lump solutions to the ($2+1$)-dimensional Sawada-Kotera equation, Nonlinear Dyn., 2017, 87, 2305-2310. doi: 10.1007/s11071-016-3190-6
CrossRef Google Scholar
|
|
[30]
|
X. Zhang and Y. Chen, Rogue wave and a pair of resonance stripe solitons to a reduced ($3+1$)-dimensional Jimbo-Miwa equation, Commun. Nonlinear. Sci. Numer. Simul., 2017, 52, 24-31. doi: 10.1016/j.cnsns.2017.03.021
CrossRef Google Scholar
|




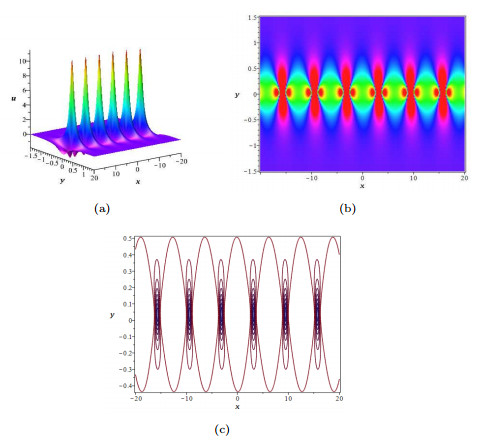

 DownLoad:
DownLoad: