| Citation: |
Jinsen Zhuang, Yan Zhou. BIFURCATIONS AND EXACT TRAVELING WAVE SOLUTIONS OF THE EQUIVALENT COMPLEX SHORT-PULSE EQUATIONS[J]. Journal of Applied Analysis & Computation, 2020, 10(2): 795-815. doi: 10.11948/20190408
|
BIFURCATIONS AND EXACT TRAVELING WAVE SOLUTIONS OF THE EQUIVALENT COMPLEX SHORT-PULSE EQUATIONS
-
Abstract
In this paper, we study the traveling wave solutions for a complex short-pulse equation of both focusing and defocusing types, which governs the propagation of ultrashort pulses in nonlinear optical fibers. It can be viewed as an analog of the nonlinear Schrödinger (NLS) equation in the ultrashort-pulse regime. The corresponding traveling wave systems of the equivalent complex short-pulse equations are two singular planar dynamical systems with four singular straight lines. By using the method of dynamical systems, bifurcation diagrams and explicit exact parametric representations of the solutions are given, including solitary wave solution, periodic wave solution, peakon solution, periodic peakon solution and compacton solution under different parameter conditions. -
-
References
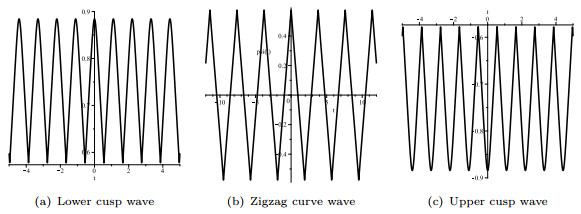
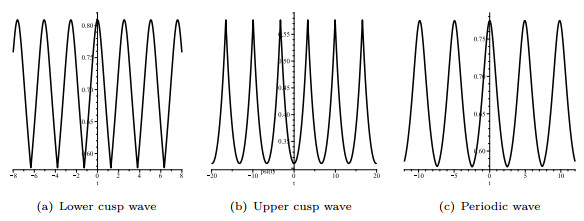
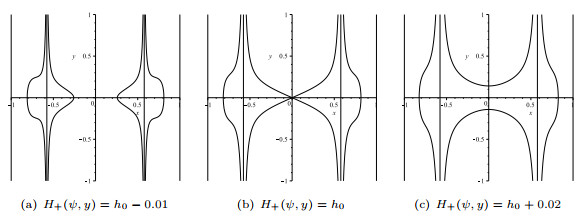
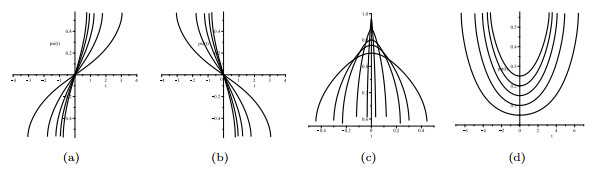
[1] J. C. Brunelli, The short pulse hierarchy, Journal of mathematical physics, 2005, 46(12), 123507. doi: 10.1063/1.2146189 [2] J. C. Brunelli, The bi-Hamiltonian structure of the short pulse equation, Physics Letters A, 2006, 353(6), 475-478. doi: 10.1016/j.physleta.2006.01.009 [3] P. F. Byrd and M. D. Friedman, Handbook of Elliptic Integrals for Engineers and Scientists, Springer, Berlin, 1971. [4] B. Feng, Complex short pulse and coupled complex short pulse equations, Physica D: Nonlinear Phenomena, 2015, 297, 62-75. doi: 10.1016/j.physd.2014.12.002 [5] B. Feng, L. Ling and Z. Zhu, Defocusing complex short-pulse equation and its multi-dark-soliton solution, Physical Review E, 2016, 93(5), 052227. doi: 10.1103/PhysRevE.93.052227 [6] V. K. Kuetche and T. C. Kofane, On two-loop soliton solution of the Schäfer- Wayne short-pulse equation using hirota's method and hodnett-moloney approach, Journal of the Physical Society of Japan, 2007, 76(2), 024004-024004. doi: 10.1143/JPSJ.76.024004 [7] J. Li, Dynamical understanding of loop soliton solution for several nonlinear wave equations, Science in China Series A: Mathematics, 2007, 50(6), 773-785. doi: 10.1007/s11425-007-0039-y [8] J. Li, Singular nonlinear travelling wave equations: Bifurcations and exact solutions, Science Press, Beijing, 2013. [9] J. Li, Variform exact one-peakon solutions for some singular nonlinear traveling wave equations of the first kind, International Journal of Bifurcation and Chaos, 2014, 24(12), 1450160. doi: 10.1142/S0218127414501600 [10] J. Li and G. Chen, On a class of singular nonlinear traveling wave equations, International Journal of Bifurcation and Chaos, 2007, 17(11), 4049-4065. doi: 10.1142/S0218127407019858 [11] J. Li and Z. Qiao, Peakon, pseudo-peakon, and cuspon solutions for two generalized camassa-holm equations, Journal of mathematical physics, 2013, 54(12), 123501. doi: 10.1063/1.4835395 [12] Y. Matsuno, Multiloop soliton and multibreather solutions of the short pulse model equation, Journal of the Physical Society of Japan, 2007, 76(8), 084003. doi: 10.1143/JPSJ.76.084003 [13] Y. Matsuno, Periodic solutions of the short pulse model equation, Journal of Mathematical Physics, 2008, 49(7), 073508. doi: 10.1063/1.2951891 [14] E. Parkes, Some periodic and solitary travelling-wave solutions of the shortpulse equation, Chaos, Solitons & Fractals, 2008, 38(1), 154-159. [15] A. Sakovich and S. Sakovich, The short pulse equation is integrable, Journal of the Physical Society of Japan, 2005, 74(1), 239-241. doi: 10.1143/JPSJ.74.239 [16] A. Sakovich and S. Sakovich, Solitary wave solutions of the short pulse equation, Journal of Physics A: Mathematical and General, 2006, 39(22), L361. doi: 10.1088/0305-4470/39/22/L03 [17] T. Schäfer and C. Wayne, Propagation of ultra-short optical pulses in cubic nonlinear media, Physica D: Nonlinear Phenomena, 2004, 196(1-2), 90-105. doi: 10.1016/j.physd.2004.04.007 [18] S. Shen, B. Feng and Y. Ohta, From the real and complex coupled dispersionless equations to the real and complex short pulse equations, Studies in Applied Mathematics, 2016, 136(1), 64-88. doi: 10.1111/sapm.12092 [19] J. Song and J. Li, Bifurcations and exact travelling wave solutions for a shallow water wave model with a non-stationary bottom surface, Journal of Applied Analysis and Computation, 2020, 10(1), 350-360. [20] A. Yariv and Y. Pochi, Optical waves in crystals: propagation and control of laser radiation, Wiley, New York, 1984. [21] P. Yu, M. Han and Y. Bai, Dynamics and bifurcation study on an extended lorenz system, Journal of Nonlinear Modelling Analysis, 2019, 1(1), 107-128. [22] Y. Zhou, J. Song and T. Han, Solitary waves, periodic peakons, pseudo-peakons and compactons given by three ion-acoustic wave models in electron plasmas, Journal of Applied Analysis and Computation, 2019, 9(2), 810-828. -
-
Figures(10)
Export File
Citation
Jinsen Zhuang, Yan Zhou. BIFURCATIONS AND EXACT TRAVELING WAVE SOLUTIONS OF THE EQUIVALENT COMPLEX SHORT-PULSE EQUATIONS[J]. Journal of Applied Analysis & Computation, 2020, 10(2): 795-815. doi: 10.11948/20190408
Format
Content
DownLoad:
-
Figure 1. Bifurcations of phase portraits of system (1.9) in the
$ (\psi, y) $ -phase plane for a fixed$ \beta>0 $ -
Figure 2. Some level curves of system (1.9) defined by
$ H_+(\psi, y) = h $ -
Figure 3. Two solitary wave solutions of system (1.9) given by
$ H_+(\psi, y) = h_3 $ when$ \delta = -1.12 $ -
Figure 4. Solitary wave, peakon and periodic peakon of system (1.9) given by
$ H_+(\psi, y) = h_s $ -
Figure 5. Some level curves of system (1.9) defined by
$ H_+(\psi, y) = h_s $ -
Figure 6. Periodic peakon solutions of system (1.9) given by
$ H_+(\psi, y) = h_s $ -
Figure 7. Periodic solutions of system (1.9) given by
$ H_+(\psi, y) = h_s $ -
Figure 8. Some level curves of system (1.9) defined by
$ H_+(\psi, y) = h $ -
Figure 9. Compacton solution families of system (1.9) defined by
$ H_+(\psi, y) = h $ -
Figure 10. Bifurcations of phase portraits of system (1.10) in the
$ (\psi, y) $ -phase plane