| Citation: |
Temesgen Desta Leta, Wenjun Liu, Abdelfattah El Achab. DYNAMICS OF SINGULAR TRAVELING WAVE SOLUTIONS OF A SHORT CAPILLARY-GRAVITY WAVE EQUATION[J]. Journal of Applied Analysis & Computation, 2021, 11(3): 1191-1207. doi: 10.11948/20200032
|
DYNAMICS OF SINGULAR TRAVELING WAVE SOLUTIONS OF A SHORT CAPILLARY-GRAVITY WAVE EQUATION
-
Abstract
In this paper, dynamical behaviour of traveling wave solutions to a short capillary-gravity equation is analyzed by using the method of bifurcation. When the phase orbits intersects the singular parabola $ y^2 = 2\phi/\lambda $ on the phase plane, then the trajectories create a weaker wave fronts than the regular traveling wave solutions. By using proper Euler transformations, we reformulate the model as a singular chaotic problem, which can then be analyzed using the singularity study. We prove existence of three types of physically realistic traveling wave solutions to the case of small diffusion for the first time, two-peaked solitary waves, three-peaked and multi-peaked periodic wave solutions.
-
-
References
[1] T. B. Benjamin, J. L. Bona and J. J. Mahony, Model equations for long waves in nonlinear dispersive systems, Philos. Trans. R. Soc. London, Ser. A, 1972, 272, 47-78. doi: 10.1098/rsta.1972.0032 [2] C. H. Borzi, R. A. Kraenkel, M. A. Manna and A. Pereira, Nonlinear dynamics of short traveling capillary-gravity waves, Phys. Rev. E, 2005, 71, 0263071-9. [3] P. F. Byrd and M. D. Fridman, Handbook of Elliptic Integrals for Engineers and Scientists, Springer, Berlin, 1971. [4] R. Camassa and D. D. Holm, An integrable shallow water equation with peaked solitons, Phys. Rev. Lett., 1993, 71, 1661-1664. doi: 10.1103/PhysRevLett.71.1661 [5] A. Chen and et al. Effects of quadratic singular curves in integrable equations, Stud. Appl. Math., 2015, 134, 24-61. [6] A. Das and A. Ganguly, Existence and stability of dispersive solutions to the Kadomtsev-Petviashvili equation in the presence of dispersion effect, Commun. Nonlin. Sci. Numer. Simulat, 2017, 48, 326-339. doi: 10.1016/j.cnsns.2016.12.032 [7] A. Das, N. Ghosh and K. Ansari, Bifurcation and exact traveling wave solutions for dual power Zakharov-Kuznetsov-Burgers equation with fractional temporal evolution, Comp. & Math. with Appl., 2018, 75(1), 59-69. [8] H. R. Dullin, G. Gottwald and D. D. Holm, An integrable shallow water equation with linear and non-linear dispersion, Phys. Rev. Lett., 2001, 87, 4501-4504. [9] A. S. Fokas and Q. Liu, Asymptotic integrability of water waves, Phys. Rev. Lett., 1996, 77, 2347-2351. doi: 10.1103/PhysRevLett.77.2347 [10] A. Geyer and M. Víctor, Singular solutions for a class of traveling wave equations arising in hydrodynamics, NonlinearAnal. RWA, 2016, 31, 57-76. doi: 10.1016/j.nonrwa.2016.01.009 [11] A. E. Green, N. Laws and P. M. Nagdhi, On the theory of water waves, Proc. R. Soc. London, Ser. A, 1974, 338, 43-55. doi: 10.1098/rspa.1974.0072 [12] A. E. Green and P. M. Naghdi, A derivation of equations for wave propagation in water of variable depth, J. Fluid Mech., 1976, 78, 237-246. doi: 10.1017/S0022112076002425 [13] R. Hakl and M. Zamora, Periodic solutions to second-order indefinite singular equations, J. Differential Equations, 2017, 263(1), 451-469. doi: 10.1016/j.jde.2017.02.044 [14] D. Korteweg and G. de Vries, On the change of form of long waves advancing in a rectangular channel and a new type of long stationary waves, Philos. Mag., 1895, 39, 422-443. doi: 10.1080/14786449508620739 [15] T. D. Leta and J. Li, Dynamical behavior of traveling wave solutions of a long waves-short waves resonance model, Qual. Theory Dyn. Syst., 2018, 27, 1750129. doi: 10.1007/s12346-018-0310-3 [16] J. Li, Singular Nonlinear Traveling Wave Equations: Bifurcations and Exact Solutions, Science, Beijing, 2013. [17] J. Li and G. Chen, On a class of singular nonlinear traveling wave equations, Int. J. Bifurcation and Chaos, 2007, 17, 4049-4065. doi: 10.1142/S0218127407019858 [18] M. A. Manna and V. Merle, Modified Korteweg-De Vries hierarchies in multiple-time variables and the solutions of modified Boussinesq equations, Proc Math. Phys. Engin. Sci., 1998, 454, 1445-1456. doi: 10.1098/rspa.1998.0215 [19] M. A. Manna and A. Neveu, A singular integrable equation from short capillary-gravity waves, preprint arXiv: physics/0303085(2003) 1-4. [20] O. Nwogu, Alternative form of Boussinesq equations for near shore wave propagation, J. Waterway, Port, Coastal, Ocean Engng, ASCE, 1993, 119, 618-638. doi: 10.1061/(ASCE)0733-950X(1993)119:6(618) [21] R. A. Seadawy, D. Lu and M. A. Khater, Bifurcations of solitary wave solutions for the three dimensional Zakharov-Kuznetsov-Burgers equation and Boussinesq equation with dual dispersion, Optik, 2017, 143, 104-114. doi: 10.1016/j.ijleo.2017.06.020 -
-
Figures(10)
Export File
Citation
Temesgen Desta Leta, Wenjun Liu, Abdelfattah El Achab. DYNAMICS OF SINGULAR TRAVELING WAVE SOLUTIONS OF A SHORT CAPILLARY-GRAVITY WAVE EQUATION[J]. Journal of Applied Analysis & Computation, 2021, 11(3): 1191-1207. doi: 10.11948/20200032
Format
Content
DownLoad:
-
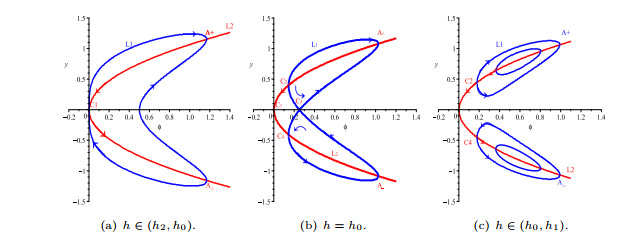
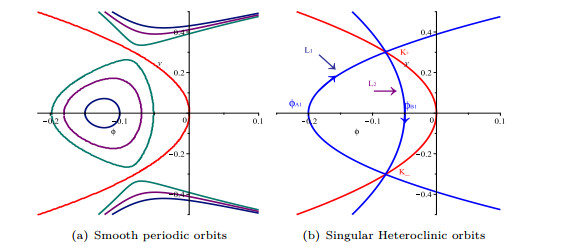
Figure 1. Bifurcations of phase portraits of system (2.2) when
$ \rho>0 $ and$ \lambda<0. $ -
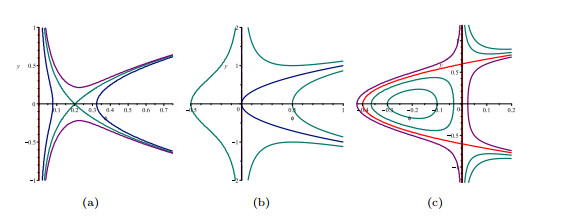
Figure 2. Bifurcations of phase portraits of system (2.2) when
$ \rho<0 $ and$ \lambda>0. $ -
Figure 3. Bifurcations of phase portraits of system (2.2) when
$ \rho<0 $ and$ \lambda\geq0. $ -
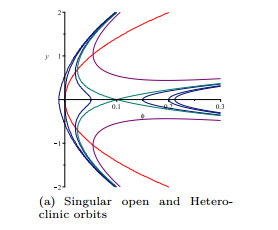
Figure 4. Bifurcations of phase portraits of system (2.2) when
$ \rho\rightarrow0 $ and$ \lambda = 0. $ -
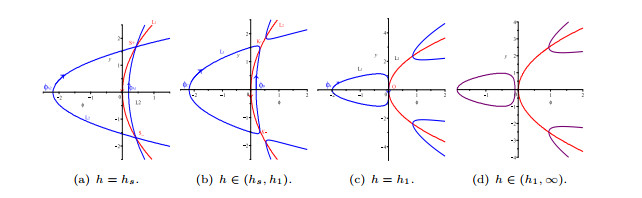
Figure 5. Bifurcations of phase portraits of system (8) when
$ \rho>0 $ and$ \lambda>0. $ -
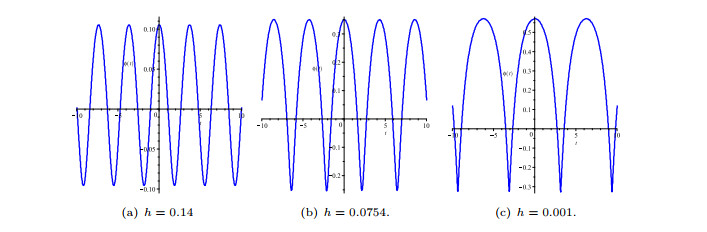
Figure 6. As
$ h\rightarrow0, $ a smooth periodic wave evolved into singular periodic wave. - Figure 7. Wave profile corresponding to exact wave solution of Eq. (3.10).
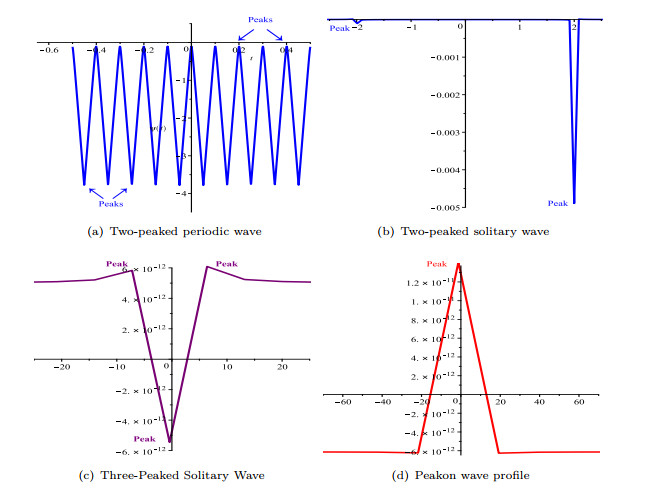
- Figure 8. Wave profiles of system (2.2)
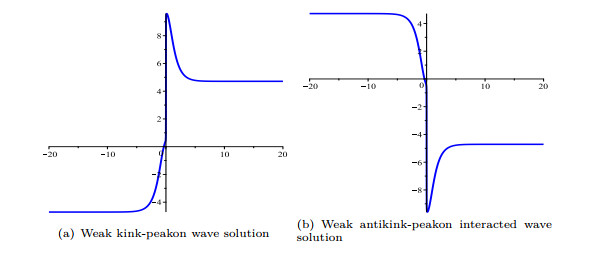
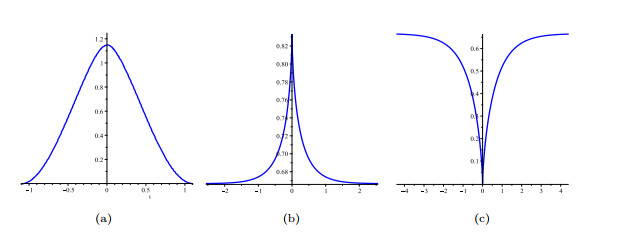
- Figure 9. Traveling wave solution of system (2.5). 9(a) A breaking wave of Eq. (3.43); 9(b) A peakon wave solution and 9(c) An anti-peakon wave solution of Eq. (3.44)
-
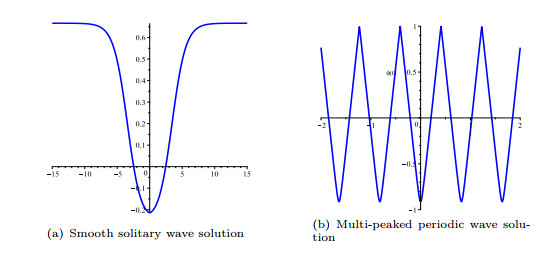
Figure 10. As
$ h $ goes from$ h_0 $ $ \rightarrow $ $ h_s, $ the smooth solitary wave evolves into a singular periodic wave.