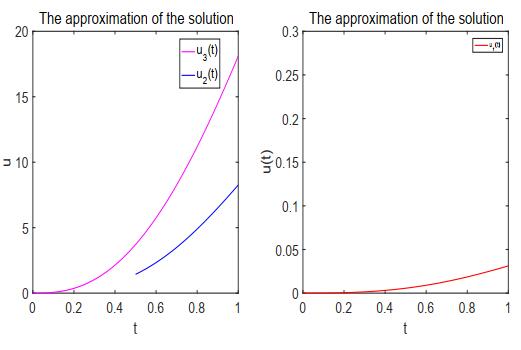
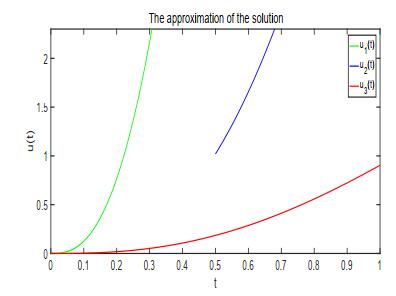
|
[1]
|
B. Ahmad, N. Alghamdi, A. Alsaedi et al., On multi-term fractional differential equations with multi-point boundary conditions, Eur. Phys. J. Spec. Top., 2017, 226, 3369-3390. doi: 10.1140/epjst/e2018-00009-3
CrossRef Google Scholar
|
|
[2]
|
R. Avery and A. Peterson, Three positive fixed points of nonlinear operators on ordered Banach spaces, Comput. Math. Appl., 2001, 42, 313-322. doi: 10.1016/S0898-1221(01)00156-0
CrossRef Google Scholar
|
|
[3]
|
D. E. Betancur-Herrera and N. Munoz-Galeano, A numerical method for solving Caputo's and Riemann-Liouville's fractional differential equations which includes multi-order fractional derivatives and variable coefficients, Commun. Nonlinear Sci. Numer. Simulat., in Press.
Google Scholar
|
|
[4]
|
A. H. Bhrawy, Y. A. Alhamed, D. Baleanu et al., New spectral techniques for systems of fractional differential equations using fractional-order generalized Laguerre orthogonal functions, Fract. Calc. Appl. Anal., 2014, 17, 1137-1157.
Google Scholar
|
|
[5]
|
C. Chen, Y. Su and Z. Feng, Positive solutions of fractional differential equations with derivative terms, Electron. J. Differ. Equ., 2012, 2012, 1-27. doi: 10.1186/1687-1847-2012-1
CrossRef Google Scholar
|
|
[6]
|
C. Goodrich, Existence of a positive solution to a class of fractional differential equations, Appl. Math. Lett., 2010, 23, 1050-1055. doi: 10.1016/j.aml.2010.04.035
CrossRef Google Scholar
|
|
[7]
|
D. Guo and V. Lakshmikantham, Nonlinear Problems in Abstract Cones, Academic Press, San Diego, 1988.
Google Scholar
|
|
[8]
|
K. Jong, H. Choi and Y. Ri, Existence of positive solutions of a class of multipoint boundary value problems for p-Laplacian fractional differential equations with singular source terms, Commun. Nonlinear Sci. Numer. Simulat., 2019, 72, 272-281. doi: 10.1016/j.cnsns.2018.12.021
CrossRef Google Scholar
|
|
[9]
|
A. Kilbas, V. Srivastava and J. Trujillo, Theory and Applications of Fractional Differential Equations, Elsevier, Amsterdam, 2006.
Google Scholar
|
|
[10]
|
R. Luca, On a class of nonlinear singular Riemann-Liouville fractional differential equations, Results Math., 2018, 125, 1-15.
Google Scholar
|
|
[11]
|
I. Masahiro and S. Motohiro, Sharp upper bound for lifespan of solutions to some critical semilinear parabolic, dispersive and hyperbolic equations via a test function method, Nonlinear Anal., 2019, 182, 57-74. doi: 10.1016/j.na.2018.12.009
CrossRef Google Scholar
|
|
[12]
|
S. Migorski and S. Zeng, Mixed variational inequalities driven by fractional evolutionary equations, Acta Math. Appl. Sin., 2019, 39B(2), 461-468.
Google Scholar
|
|
[13]
|
K. Miller and B. Ross, An Introduction to the Fractional Calculus and Fractional Differential Equations, John Wiley and Sons, Inc, New York, 1993.
Google Scholar
|
|
[14]
|
U. R. Mujeeb, A. K. Rahmat and A. A. Naseer, Three point boundary value problems for nonlinear fractional differential equations, Acta Math. Sci., 2011, 31B(4), 1337-1346.
Google Scholar
|
|
[15]
|
I. Podlubny, Fractional Differential Equations, Academic Press, San Diego, 1999.
Google Scholar
|
|
[16]
|
J. Ren, W. Ge and B. Ren, Existence of three solutions for quas-linear boundary value problems, Acta Math. Appl. Sin., 2005, 21, 353-358. doi: 10.1007/s10255-005-0242-y
CrossRef Google Scholar
|
|
[17]
|
Y. Su, Multiple positive pseudo-symmetric solutions of p-Laplacian dynamic equations on time scales, Math. Comput. Model., 2009, 49, 1664-1681. doi: 10.1016/j.mcm.2008.10.010
CrossRef Google Scholar
|
|
[18]
|
Y. Su and Z. Feng, Existence theory for an arbitrary order fractional differential equation with deviating argument. Acta Appl. Math., 2012, 112, 81-105.
Google Scholar
|
|
[19]
|
Y. Su and Z. Feng, Existence of pseudo-symmetric solutions to a p-Laplacian four-point BVPs involving derivatives on time scales, Differ. Integal. Equ., 2012, 25, 441-466.
Google Scholar
|
|
[20]
|
Y. Su, Y. Yun and D. Wang, Existence of solutions to nonlinear p-Laplacian fractional differential equations with higher-order derivative term, Electron. J. Differ. Equ., 2018, 2018, 1-24. doi: 10.1186/s13662-017-1452-3
CrossRef Google Scholar
|
|
[21]
|
B. Vanessa, D. M. Roger and S. Gleison, Local well-posedness for the nonlocal derivative nonlinear Schrödinger equation in Besov spaces, Nonlinear Anal., 2019, 187, 320-338. doi: 10.1016/j.na.2019.05.005
CrossRef Google Scholar
|
|
[22]
|
P. Verma, I. Wong and N. A. Melosh, Continuum model of mechanical interactions between biological cells and artificial nanostructures, Biointerphases, 2010, 5, 37-44. doi: 10.1116/1.3431960
CrossRef Google Scholar
|
|
[23]
|
Y. Wei, Q. Song and Z. Bai, Existence and iterative method for some fourth order nonlinear boundary value problems, Appl. Math. Lett., 2019, 87, 101-107. doi: 10.1016/j.aml.2018.07.032
CrossRef Google Scholar
|
|
[24]
|
M. Xiang, B. Zhang and D. Yang, Mmultiplicity results for variable-order fractional Laplacian equations with variable growth, Nonlinear Anal., 2019, 178, 190-204. doi: 10.1016/j.na.2018.07.016
CrossRef Google Scholar
|
|
[25]
|
M. Xu and S. Sun, Positivity for integral boundary value problems of fractional differential equations with two nonlinear terms, Appl. Math. Comput., 2019, 59, 271-283.
Google Scholar
|
|
[26]
|
X. Yang, Z. Wei and W. Dong, Existence of positive solutions for the boundary value problem of nonlinear fractional differential equations, Commun. Nonlinear Sci. Numer. Simulat., 2012, 17, 85-92. doi: 10.1016/j.cnsns.2011.05.007
CrossRef Google Scholar
|
|
[27]
|
Y. Yun, Y. Su and W. Hu, Existence and uniqueness of solutions to a class of anti-periodic boundary value problem of fractional differential equations with p-Laplacian operator. Acta Math. Sci., 2018, 38, 1161-1172.
Google Scholar
|
|
[28]
|
S. Zhang, Positive solutions to singular boundary value problem for nonlinear fractional differential equation, Comput. Math. Appl., 2010, 59, 1300-1309. doi: 10.1016/j.camwa.2009.06.034
CrossRef Google Scholar
|
|
[29]
|
K. V. Zhukovsky, The operational solution of fractional-order differential equations, as well as BlackScholes and heat-conduction equations, Moscow Univ. Phys., 2016, 71, 237-244. doi: 10.3103/S0027134916030164
CrossRef Google Scholar
|




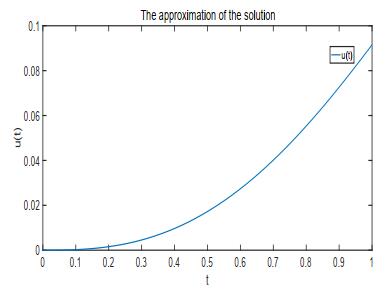

 DownLoad:
DownLoad: