| Citation: |
Qiannan Song, Ruizhi Yang, Chunrui Zhang, Lei Wang. BIFURCATION ANALYSIS OF A DIFFUSIVE PREDATOR-PREY MODEL WITH BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE[J]. Journal of Applied Analysis & Computation, 2021, 11(2): 920-936. doi: 10.11948/20200119
|
BIFURCATION ANALYSIS OF A DIFFUSIVE PREDATOR-PREY MODEL WITH BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE
-
Abstract
In this paper, we consider a diffusive predator-prey model with Beddington-DeAngelis functional response. The Turing instability and Hopf bifurcation of the coexisting equilibrium are investigated. We also use bifurcation parameters $ m, {d_2} $ to study the Turing-Hopf bifurcation. In addition, we compute the normal form for the Turing-Hopf bifurcation. On the basis of the corresponding normal form, there exists complex spatiotemporal dynamics near Turing-Hopf bifurcation point. Finally, Some numerical simulations are given to illustrate our theoretical results.
-
Keywords:
- Predator-prey /
- Turing instability /
- Hopf bifurcation /
- Turing-Hopf bifurcation
-
-
References
[1] C. Arancibia-Ibarra, J. D. Flores, G. J. Pettet, et al, A Holling-Tanner Predator-Prey Model with Strong Allee Effect, International Journal of Bifurcation & Chaos, 2019, 29(11), 1930032. [2] J. R. Beddington, Mutual Interference Between Parasites or Predators and its Effect on Searching Efficiency, Journal of Animal Ecology, 1975, 44(1), 331-340. doi: 10.2307/3866 [3] P. H. Crowley and E. K. Martin, Functional Responses and Interference within and between Year Classes of a Dragonfly Population, Journal of the North American Benthological Society, 1989, 8(3), 211-221. doi: 10.2307/1467324 [4] S. Djilali, Effect of herd shape in a diffusive predator-prey model with time delay, Journal of Applied Analysis and Computation, 2019, 9(2), 638-654. doi: 10.11948/2156-907X.20180136 [5] M. Falconi, Y. Vera-Damian and C. Vidal, Predator interference in a Leslie-Gower intraguild predation model, Nonlinear Analysis Real World Applications, 2019, 51, 102974. [6] S. Gakkhar and R. K. Naji, Seasonally perturbed prey-predator system with predator-dependent functional response, Chaos Solitons & Fractals, 2003, 18(5), 1075-1083. [7] C. S. Holling, The Functional Response of Predators to Prey Density and its Role in Mimicry and Population Regulation, Memoirs of the Entomological Society of Canada, 1965, 97(45), 1-60. [8] M. P. Hassell and G. C. Varley, New inductive population model for insect parasites and its bearing on biological control, Nature, 1969, 223(5211), 1133-1137. doi: 10.1038/2231133a0 [9] H. Jiang and X. Tang, Hopf bifurcation in a diffusive predator-prey model with herd behavior and prey harvesting, Journal of Applied Analysis and Computation, 2019, 9(2), 671-690. doi: 10.11948/2156-907X.20180142 [10] W. Jiang, Q. An and J. Shi, Formulation of the normal forms of Turing-Hopf bifurcation in reaction-diffusion systems with time delay, 2018, arXiv: 1802.10286. [11] W. Jiang, H. Wang and X. Cao, Turing instability and Turing-Hopf bifurcation in diffusive Schnakenberg systems with gene expression time delay, Journal of Dynamics and Differential Equations, 2019, 31(4), 2223-2247. doi: 10.1007/s10884-018-9702-y [12] X. Jiang, Z. She, Z. Feng, et al, Bifurcation Analysis of a Predator-Prey System with Ratio-Dependent Functional Response. International Journal of Bifurcation Chaos, 2018, 27(14), 1750222. [13] S. Khajanchi, Modeling the dynamics of stage-structure predator-prey system with Monod-Haldane type response function, Applied Mathematics & Computation, 2017, 302, 122-143. [14] P. Mishra, S. N. Raw and B. Tiwari, Study of a Leslie-Gower predator-prey model with prey defense and mutual interference of predators, Chaos Solitons & Fractals, 2019, 120, 1-16. [15] G. D. Ruxton, W. S. C. Gurney and A. M. D. Roos, Interference and generation cycles, Theoretical Population Biology, 1992, 42(3), 235-253. doi: 10.1016/0040-5809(92)90014-K [16] G. T. Skalski and J. F. Gilliam, Functional responses with predator interference: viable alternatives to the Holling type Ⅱ model, Ecology, 2001, 82(11), 3083-3092. doi: 10.1890/0012-9658(2001)082[3083:FRWPIV]2.0.CO;2 [17] J. Song, Nonexistence of Nonconstant Positive SteadyStates of a Diffusive Predator-prey Model withFear Effect, Journal of Nonlinear Modeling and Analysis, 2020, 2(3), 317-332. [18] M. Song, W. Zuo, D. Jiang, et al, Stationary Distribution and Extinction of Stochastic Beddington-DeAngelis Predator-prey Model with Distributed Delay, Journal of Nonlinear Modeling and Analysis, 2020, 2(2), 187-204. [19] Y. Song, H. Jiang and Y. Yuan, Turing-Hopf bifurcation in the reactiondiffusion system with delay and application to a diffusive predator-prey model, Journal of Applied Analysis and Computation, 2019, 9(3), 1132-1164. doi: 10.11948/2156-907X.20190015 [20] Y. Song, T. Zhang and Y. Peng, Turing-Hopf bifurcation in the reaction-diffusion equations and its applications, Communications in Nonlinear Science & Numerical Simulation, 2016, 33(4), 229-258. [21] W. Tan, W. Yu, T. Hayat, et al, Turing Instability and Bifurcation in a Diffusion Predator-Prey Model with Beddington-DeAngelis Functional Response, International Journal of Bifurcation & Chaos, 2018, 28(9), 1830029. [22] D. Xiao, H. Zhu, Multiple Focus and Hopf Bifurcations in a Predator-Prey System with Nonmonotonic Functional Response, Siam Journal on Applied Mathematics, 2006, 66(3), 802-819. doi: 10.1137/050623449 [23] H. Xu and S. Fu, Density-dependent effects on Turing patterns and steady state bifurcation in a Beddington-DeAngelis-type predator-prey model, Boundary Value Problems, 2019, 2019(1). doi: 10.1186/s13661-019-1214-0/fulltext.html [24] X. Yan and C. Zhang, Stability and turing instability in a diffusive predator-prey system with Beddington-DeAngelis functional response, Nonlinear Analysis Real World Applications, 2014, 20, 1-13. doi: 10.1016/j.nonrwa.2014.04.001 [25] T. Zhang, T. Xu, J. Wang, et al, Homoclinic Cycle and Homoclinic Bifurcations of a Predator-prey Model with Impulsive State Feedback Control, Journal of Nonlinear Modeling and Analysis, 2020, 2(2), 227-240. [26] X. Zhang, Q. Zhang and V. Sreeram, Bifurcation analysis and control of a discrete harvested prey-predator system with Beddington-DeAngelis functional response, Journal of the Franklin Institute, 2010, 347(7), 1076-1096. doi: 10.1016/j.jfranklin.2010.03.016 -
-
Figures(7)
Export File
Citation
Qiannan Song, Ruizhi Yang, Chunrui Zhang, Lei Wang. BIFURCATION ANALYSIS OF A DIFFUSIVE PREDATOR-PREY MODEL WITH BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE[J]. Journal of Applied Analysis & Computation, 2021, 11(2): 920-936. doi: 10.11948/20200119
Format
Content
DownLoad:
-
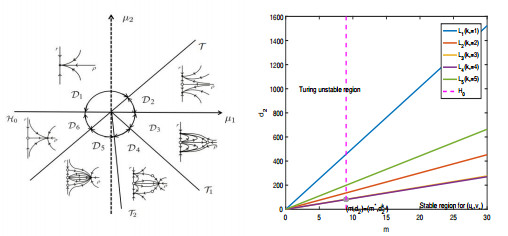
Figure 1. Left: the bifurcation diagram. Right: Stable region for
$ (u_*, v_*) $ , Turing-Hopf bifurcation point$ (m^*, d_2^{k_*}) $ in$ m-d_2 $ plane. -
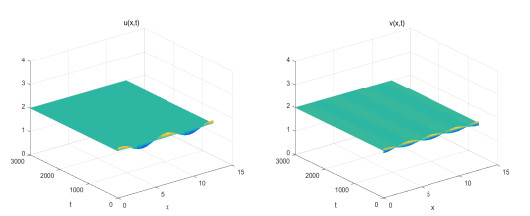
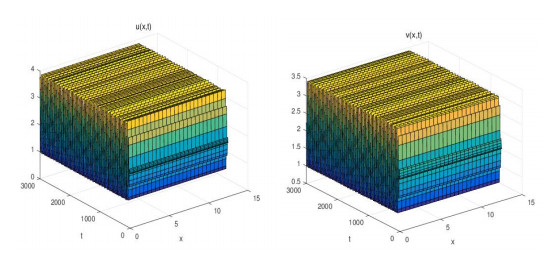
Figure 2. For
$ \left( {{\mu _1}, {\mu _2}} \right) = \left( {0.1, 1.0} \right) \in {D_1} $ , the positive equilibrium$ (u_*, v_*) $ of the system (2.1) is asymptotically stable. -
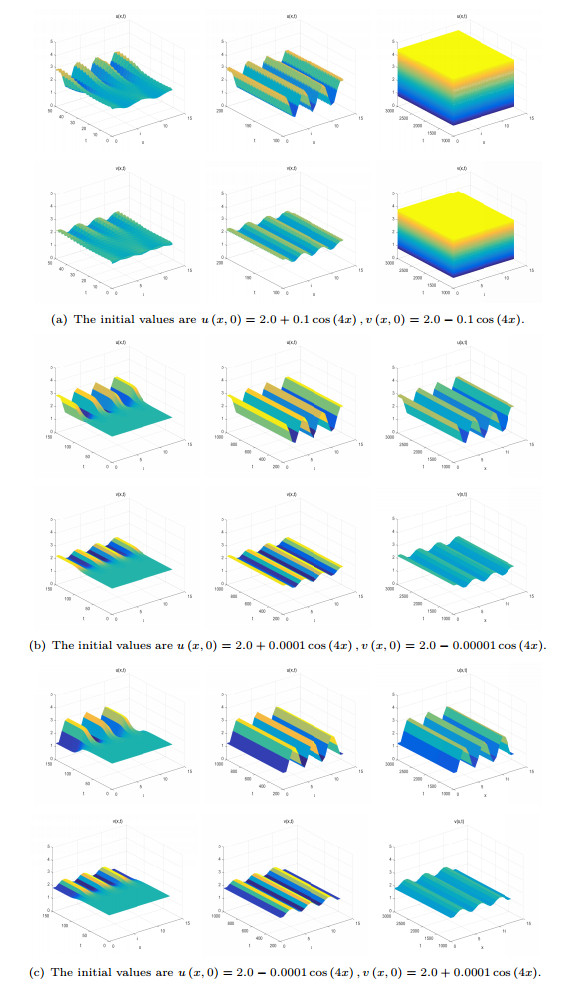
Figure 3. For
$ \left( {{\mu _1}, {\mu _2}} \right) = \left( {1.0, 0.1} \right) \in {D_2} $ , there is a pair of stable spatially inhomogeneous steady states. -
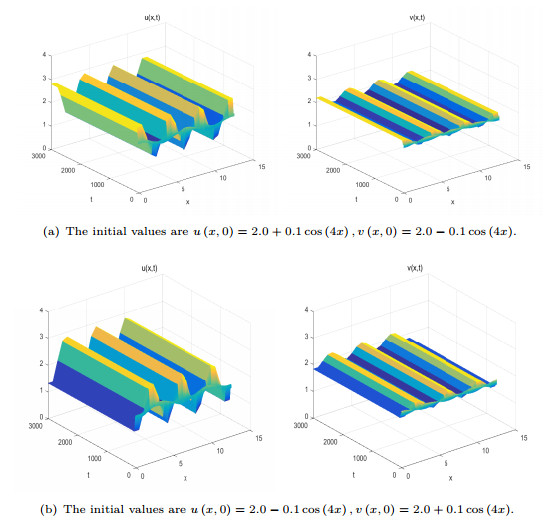
Figure 4. For
$ \left( {{\mu _1}, {\mu _2}} \right) = \left( {1.0, -0.1} \right) \in {D_3} $ , the system (2.1) has a pair of stable spatially inhomogeneous steady states and an unstable spatially homogeneous periodic solution. -
Figure 5. When
$ \left( {{\mu _1}, {\mu _2}} \right) = \left( {1.0, -0.2} \right) \in {D_4} $ , there exists a stable spatially homogeneous periodic solution and a pair of stable spatially inhomogeneous steady states, as well as a pair of unstable spatially inhomogeneous periodic solutions. -
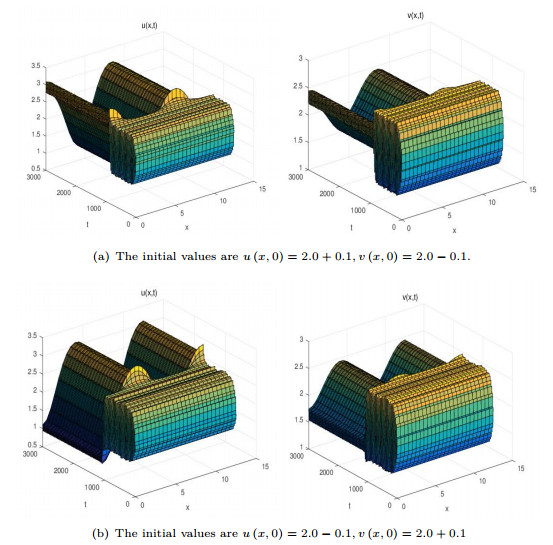
Figure 6. For
$ \left( {{\mu _1}, {\mu _2}} \right) = \left( {1.0, -2.0} \right)\in {D_5} $ , the system (2.1) has a stable spatially homogeneous periodic solution and a pair of unstable spatially inhomogeneous steady states. The initial values are$ {u\left( {x, 0} \right) = 2.0 + 0.2\cos\left( {4x} \right), v\left( {x, 0} \right) = 2.0 - 0.2\cos\left( {4x} \right)} $ . -
Figure 7. When
$ \left( {{\mu _1}, {\mu _2}} \right) = \left( {-1.0, -0.5} \right) \in {D_6} $ , there is a stable spatially homogeneous periodic solution. The initial values are$ {u\left( {x, 0} \right) = 2.0 + 0.01, v\left( {x, 0} \right) = 2.0 - 0.01} $ .