| Citation: | Yan Bai, Weihua Jiang, Yanping Guo, Yunhong Li, Yujing Liu. THE EXISTENCE OF NONTRIVIAL SOLUTION FOR BOUNDARY VALUE PROBLEM OF NONLINEAR FRACTIONAL DIFFERENTIAL EQUATION[J]. Journal of Applied Analysis & Computation, 2021, 11(2): 1017-1028. doi: 10.11948/20200202 |
THE EXISTENCE OF NONTRIVIAL SOLUTION FOR BOUNDARY VALUE PROBLEM OF NONLINEAR FRACTIONAL DIFFERENTIAL EQUATION
-
Abstract
By using the theory of degree, the existence of nontrivial solution for boundary value problem of nonlinear fractional differential equation is investigated. In order to get this conclusion, we make use of Laplace transform to obtain the conditions that the eigenvalues satisfy. Then, for three different specific problems, we use Matlab software to calculate the eigenvalues. This is the fundamental skill that Leray-Schauder degree theorem can be used.
-

-
References
[1] B. Ahmad and A. Alsaedi, Existence of solutions for anti-periodic boundary value problems of nonlinear impulsive functional integro-differential equations of mixed type, Nonlinear. Anal-Hybri, 2010, 3(4), 501-509. [2] Z. Bai and H. Lü, Positive solutions for boundary value problem of nonlinear fractional differential equation, J. Math. Anal. Appl, 2005, 2005(311), 495-505. [3] A. Cabada and G. Wang, Positive solutions of nonlinear fractional differential equations with integral boundary value conditions, J. Math. Anal. Appl, 2012, 2012(389), 403-411. [4] X. Dong, Z. Bai and S. Zhang, Positive solutions to boundary value problems of p-laplacian with fractional derivative, Bound. Value Probl, 2017, 2017(1), 1-15. doi: 10.1186/s13661-016-0733-1 [5] Y. Y. Gambo and R. Ameen, Existence and uniqueness of solutions to fractional differential equations in the frame of generalized caputo fractional derivatives, Adv. Differ. Equ, 2018, 2018(1), 134. doi: 10.1186/s13662-018-1594-y [6] D. Guo and V. akshmikantham, Nonlinear Problems in Abstract Cones, Academic Press, San Diego, 1988. [7] H. J. Haubold, A. M. Mathai and R. K. Saxena, Mittag-leffler functions and their applications, J. Appl. Math, 2011, 2011, 36-47. [8] R. Hilfer, Applications of Fractional Calculus in Physics, World Scientific, Singapore, 2000. [9] W. Jiang and N. Kosmatov, Resonant p-laplacian problems with functional boundary conditions, Bound. Value Probl, 2018, 2018(1), 72. doi: 10.1186/s13661-018-0986-y [10] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and applications of fractinal differential equations, Elsevier, Amsterdam, 2006. [11] T. Ma, Y. Tian, Q. Huo and Y. Zhang, Boundary value problem for linear and nonlinear fractional differential eqations, Appl. Math. Lett, 2018, 86, 1-7. doi: 10.1016/j.aml.2018.06.010 [12] I. Podlubny, Fractional differential equations, Academic Press, New York, 1999. [13] J. Wang, Y. Wen, Y. Gou et al., Fractional-order gradient descent learning of bp neural networks with caputo derivative, Neural Netw, 2017, 89, 19-30. doi: 10.1016/j.neunet.2017.02.007 [14] Y. Wang, Necessary conditions for the existence of positive solutions to fractional boundary value problems at resonance, Appl. Math. Lett, 2019, 97, 34-40. doi: 10.1016/j.aml.2019.05.007 [15] M. Xu and S. Sun, Positivity for integral boundary value problems of fractional differential equations with two nonlinear terms, J. Comput. Appl. Math, 2019, 59(1), 271-283. [16] X. Zhao and F. An, The eigenvalues and sign-changing solutions of a fractional boundary value problem, Adv. Differ. Equ, 2016, 109(2016), 1-8. [17] Y. Zhao, S. Sun, Z. Han and M. Zhang, Positive solutions for boundary value problems of nonlinear fractional differential equations, Appl. Math. Comput, 2011, 217(16), 6950-6958. -
-
-
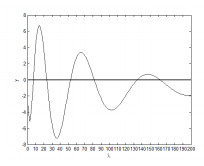
Figure 1. Graph of equation
$ f_2 $ -
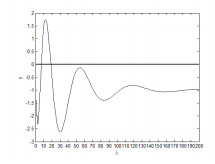
Figure 2. Graph of equation
$ f_3 $ -
Figure 3. Graph of equation
$ f_4 $




 DownLoad:
DownLoad: